芻議大數學觀視域下小學數學深度教學課堂建構策略

【摘要】大數學觀強調在數學教學中讓學生“先見林，再見樹”，建構知識體系，聚焦于對數學知識本質的理解，實現深度學習。文章以蘇教版小學數學教材為例，基于大數學觀，就小學數學深度教學課堂建構策略進行探究。

【關鍵詞】大數學觀；深度教學；“大學生觀”；“大整體觀”；“大教學觀”

【基金項目】本文系無錫市教育科學“十四五”規劃2021年度課題“基于兒童理解的小學數學深度教學的實踐研究”（批準號：B/D/2021/03）的研究成果。

作者簡介：吳超（1988—），女，江蘇省宜興市湖濱實驗學校。

張皎（1978—），女，江蘇省宜興市湖濱實驗學校。

深度教學，是指教師借助一定的活動或問題情境，帶領學生超越表層的知識符號學習，深入知識內在的邏輯和意義，挖掘知識豐富的內涵，充分實現數學知識對學生發展的作用［1］。大數學觀視域下的深度教學需要教師樹立“大學生觀”“大整體觀”“大教學觀”，從關注具體的知識點轉向關注知識體系，幫助學生真正理解知識的本質，完善知識結構，從而有效落實培養學生數學核心素養的任務。

一、樹立“大學生觀”，引導學生深度探究

了解學生學情是建構深度學習課堂的前提。教師應樹立“大學生觀”，將學生視作發展中的人，改變以往以經驗判斷學情的方式，代之以實證研究，以便準確地了解學生學情，科學地確立數學課堂的起點。教師應重視學生在深度教學課堂建構中的主體作用，發揮學生的主觀能動性，引導學生在學習中自主思考。

（一）開展有意義的數學交流，感悟知識價值

以學生為中心的課堂就是要鼓勵學生發揮主觀能動性，允許學生在數學課堂上大膽表達、相互啟發，給學生提供多元發展的可能，在最大限度內實現因材施教。

例如，在蘇教版小學數學教材二年級下冊“數據的收集與整理”的內容教學中，教師除了要傳授給學生科學有效的數據收集與整理方法，還要尊重學生的主體性，鼓勵學生在解決生活實際問題時選擇自己更熟悉、更喜歡的數據收集與整理方法。在課堂中，教師可以鼓勵學生踴躍發言，讓學生到講臺上分享自己所用到的數據收集與整理方法，展示自己的成果。同時，教師還要鼓勵其他學生就同伴的成果提出建議，使學生間產生思維的碰撞，從而激發學生對數據收集與整理活動的興趣，使學生形成數據意識。

（二）設計高質量的數學問題，強化概念理解

高質量的數學問題能夠凸顯教學重點，為突破教學難點提供思維支架。教師課堂上給學生提出高質量的數學問題，能讓學生明確探究活動的方向，抓住關鍵信息，深入理解數學概念。

例如，在蘇教版小學數學教材三年級下冊“分數”的內容教學中，針對教材內容“分桃”，教師提問：“將4個桃平均分成4份，每份是原來的幾分之幾？將8個桃平均分成4份，每份又是原來的幾分之幾？”在學生表示每份都是原來的 后，教師繼續提問：“把12個桃、20個桃、100個桃平均分成4份，每份是原來的幾分之一？”學生得出答案后，教師緊接著追問：“每盤桃的總個數不一樣，平均分成的每份的個數也不一樣，為什么每份都是原來的 呢？”幾個問題層層遞進，在關鍵處引導，在重難點處點撥，引導學生聚焦于整體平均分的份數，初步理解分數的意義。

（三）創設趣味性的情境，探究規律本質

要想在課堂上調動學生的主觀能動性，就要激發學生的學習興趣。教師可以利用信息技術創設趣味性的教學情境，加強教學內容的直觀性，促使學生主動探索數學知識。

例如，在蘇教版小學數學教材四年級下冊“三角形的三邊關系”的內容教學中，教師可以借助幾何畫板輔助教學，通過改變線段的長度和端點的位置，讓學生觀察三角形的變化。此外，教師還可以讓學生親自操作幾何畫板，將三條線段圍成三角形。學生從圖形操作中能夠更加形象地看出三角形三邊的關系，從而理解“三角形任意兩邊長度的和大于第三邊”的規律。

二、樹立“大整體觀”，促進知識深度建構

傳統教學往往缺少對學科知識體系的整體架構，導致學生接觸到的只是碎片化知識，難以形成整體認知。針對這一問題，教師應樹立“大整體觀”，從知識的統一性入手，在教學過程中逐步引導學生建構知識體系。

（一）注重知識聯結，助推經驗遷移

在教學中實現知識聯結，既要凸顯數學知識的本質，又要符合學生的心理特點。具體而言，教師要遵循學生認知結構建立的規律，重視學生已有經驗與后續發展，開展承上啟下的聯結性教學，引導學生體會知識之間的邏輯關系。

例如，在蘇教版小學數學教材五年級上冊“多邊形”的內容教學中，教師要站在大單元的角度上進行教學設計，讓學生在推導平行四邊形、三角形、梯形面積公式的過程中厘清各種圖形之間的聯系，初步建立多種平面圖形的知識結構。如此一來，在學習“圓的面積”一課時，學生就能自然地遷移運用之前的經驗，形成認知閉環，構建完整的平面圖形知識網絡。

（二）引入數學模型，促進整體建構

數學模型是運用數理邏輯方法和數學語言建構的科學或工程模型。構建數學模型能將零散的知識點或知識塊聚合成較為完整的知識面，從而引導學生充分學習，厘清知識脈絡。

例如，在蘇教版小學數學教材四年級下冊“運算律”的內容教學中，教師可以借助多媒體設備出示問題情境，引導學生主動掌握乘除法模型，如下所示。

（1）紅紅和玲玲誰走得快？

時間 路程

紅紅 2分鐘 100米

玲玲 6分鐘 400米

（2）貨車和客車哪輛車開得快？

時間 路程

貨車 3小時 180千米

客車 4小時 320千米

在討論中，學生意識到要知道誰走得快，就要算出兩人每分鐘各走多少米，要知道哪輛車開得快，就要知道它們每小時各開多少千米，由此得出速度的概念，即速度就是每小時、每分鐘、每秒等單位時間內行駛的路程。接著，教師讓學生進行計算和比較，從中梳理出路程、時間、速度的關系。學生進一步得出：速度×時間=路程，路程÷速度=時間，路程÷時間=速度。教師總結：在路程、速度、時間這三個量中，只要知道其中任意兩個量，就可以求出第三個量。最后，教師讓學生根據“速度、時間、路程”的模型梳理出其他同類模型。學生結合學過的知識，得出“單價、數量、總價”和“每份數、份數、總數”等也屬于這類模型，從而強化了模型應用意識。

（三）完善評價體系，形成教學閉環

教學評價是教學的最后一個環節，有助于教師診斷和改進教學過程中的問題，提升教學質量。教學評價的實行者可以是教師，也可以是學生。

例如，在蘇教版小學數學教材六年級下冊“分數的四則混合運算”的內容教學中，教學結束后，教師可以為學生提供自評量表，引導學生對自己的學習情況進行打分。在評價量表的設計上，教師可以加入“我能夠理解并掌握分數四則混合運算的正確順序”“我可以使用分數加法、乘法等去解決一些比較復雜的實際問題”等評價內容。要注意的是，教學評價的設計要與教學目標及教學過程相契合，從而使教學形成一個閉環。

三、樹立“大教學觀”，實現思維深度進階

“大教學觀”要求教師在教學中敢于破舊立新，以數學核心素養的培育為第一要義，尤其注重培養學生的數學思維，幫助學生實現思維的深度進階。

（一）在操作中發展思維的靈活性

為充分在數學教學中發展學生的數學思維，教師可以設計具有操作性的題目，讓學生在操作探索中解決問題。

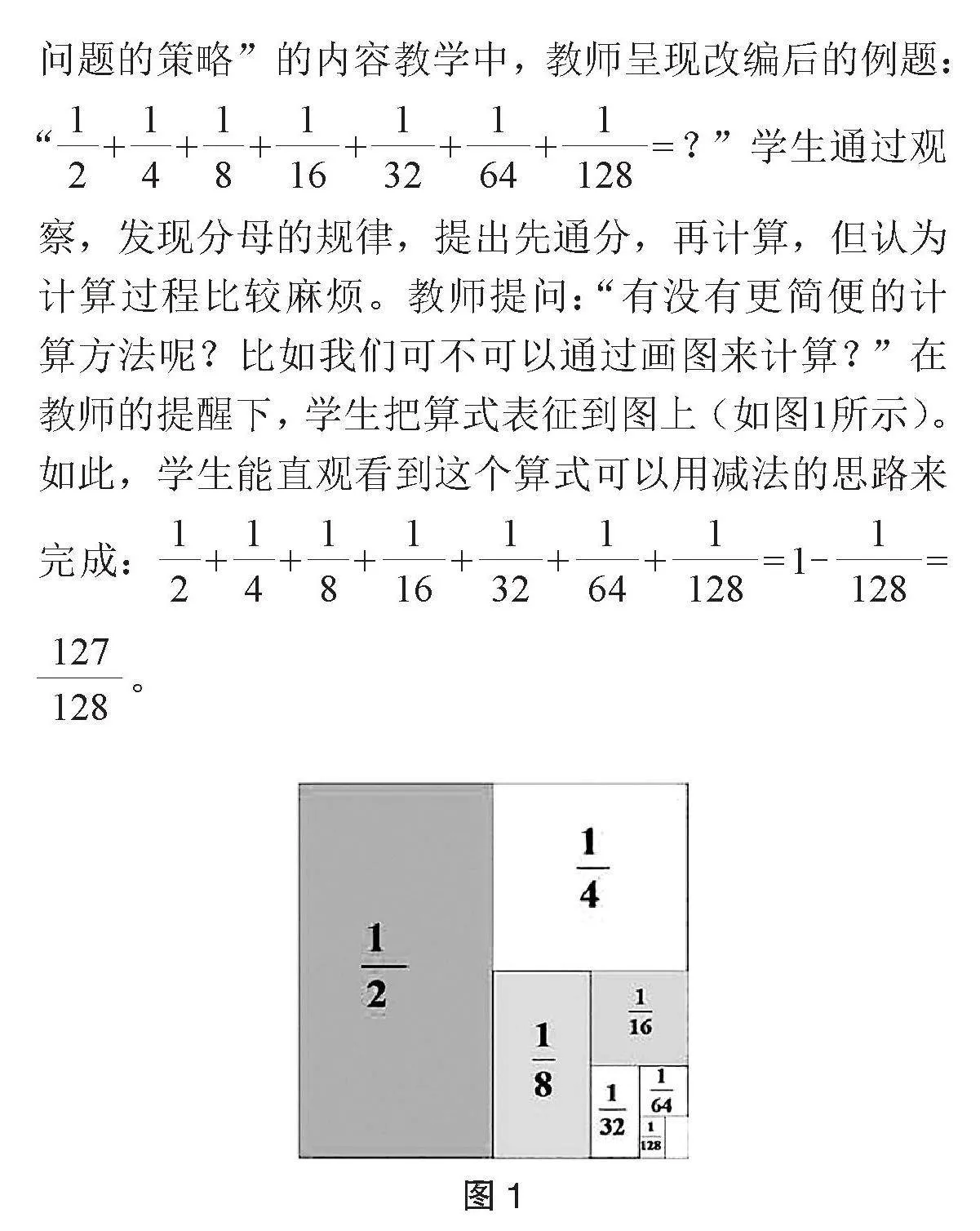
例如，在蘇教版小學數學教材五年級下冊“解決問題的策略”的內容教學中，教師呈現改編后的例題：“ + + + + + + = ？”學生通過觀察，發現分母的規律，提出先通分，再計算，但認為計算過程比較麻煩。教師提問：“有沒有更簡便的計算方法呢？比如我們可不可以通過畫圖來計算？”在教師的提醒下，學生把算式表征到圖上（如圖1所示）。如此，學生能直觀看到這個算式可以用減法的思路來完成： + + + + + + = 1- = 。

（二）在比較中發展思維的深刻性

在“大教學觀”下，數學教師要實現深度學習，還要培養學生思維的深刻性，通過設計一系列的對比練習，讓學生厘清思路，打破思維定式，學會舉一反三、觸類旁通。

例如，在蘇教版小學數學教材五年級下冊“倍數和因數”的內容教學中，教師可以設計這樣的題組練習：“（1）把長160厘米、寬100厘米的長方形紙張剪成若干個相等的小正方形，并且無剩余，最少可以剪多少個？（2）如小長方形紙片長16厘米、寬10厘米，則至少需要多少張這樣的小長方形紙片才能拼成一個正方形？”［2］這兩道題極易讓學生感到困惑，分辨不清到底應該使用公倍數還是公因數的知識來解決。教師引導學生關注題目中的關鍵詞“剪”和“拼”，動手畫一畫，相互比一比。學生發現，在第一道題中，剪出的小正方形的邊長是160和100的最大公因數；在第二道題中，拼出的大正方形的邊長是16和10的最小公倍數。學生在比較中明白原理，進一步發展了思維的深刻性。

（三）在辨析中發展思維的批判性

“大數學觀”下的深度教學還要求學生能夠批判性地分析數學問題，在質疑—思辨—探究的過程中，對數學知識的本質有更為深刻和全面的認識。

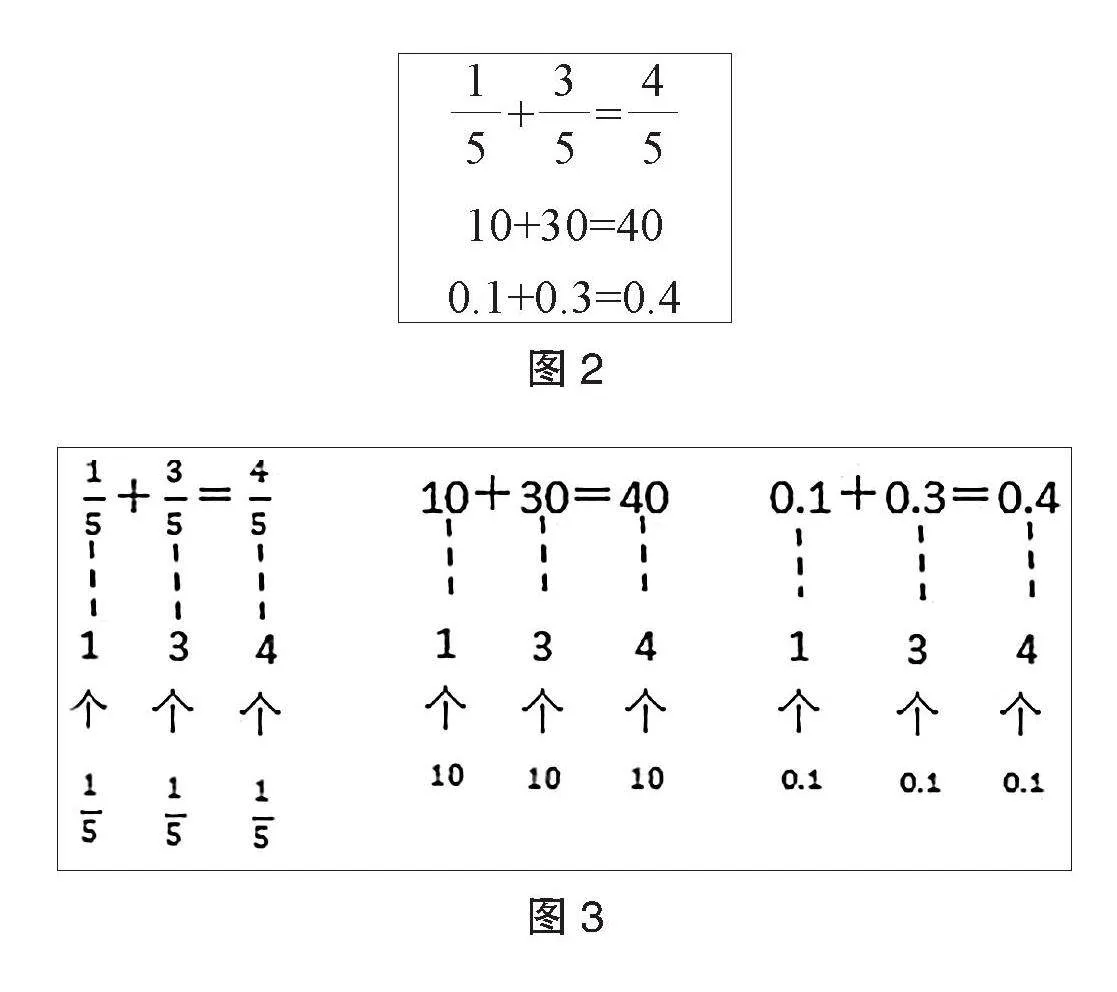
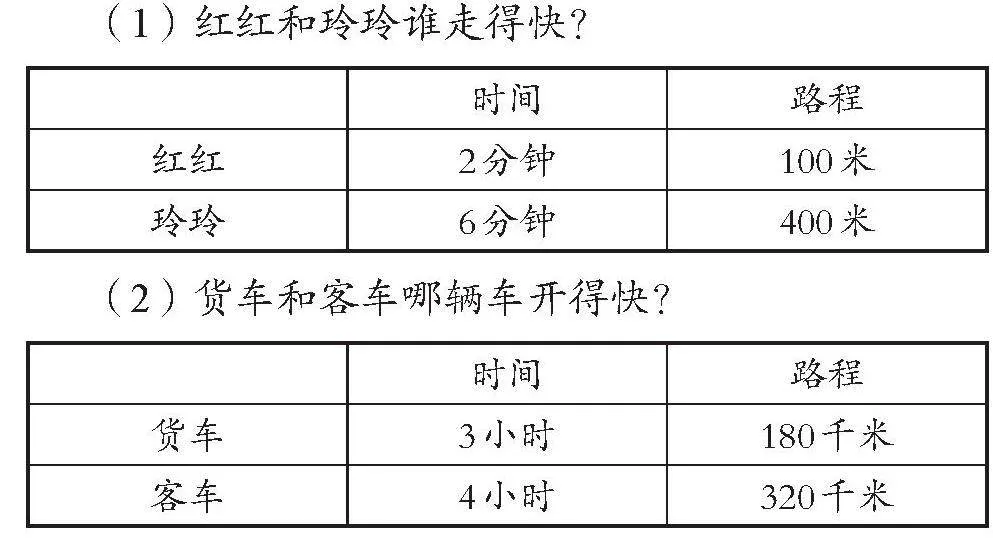
例如，在蘇教版小學數學教材五年級下冊“分數加減法”的內容教學中，教師出示不同的算式讓學生辨析，從而發展學生思維的批判性。首先，教師根據圖2讓學生討論三個算式的算法是否一致。有的學生認為分數、整數與小數的計算方法肯定不一樣，各自有相應的計算法則；有的學生認為三個算式或許是有聯系的，因為計算結果中的“4”都是由“1+3”得到的。學生進行辨析后，教師給學生提供思維支架：“每個算式中的‘1’‘3’‘4’分別表示什么呢？”如此，教師把學生辨析的聚焦點引導到計數單位上。學生將三個算式的計算思維可視化（如圖3所示），意識到雖然這三個加法算式形式不同，計數單位也不同，但計算時都需要把相同計數單位的個數進行累加，因此其計算原理是相通的。學生通過觀察、對比、質疑、討論，感悟到數的運算的一致性，增強了批判性思維，也發展了推理意識。

結語

總之，教師有深度的教是學生有深度的學的必要條件和可靠保障 ，教師要立足于大數學觀，把深度教學根植于課堂教學中，設計有助于學生深度思考的數學活動，讓學生在深度探究中理解數學知識的本質，推動數學核心素養的發展。

【參考文獻】

［1］余小芬.知識教育立場下的深度教學：以特級教師張健《分數的意義》一課為例［J］.教育研究與評論（小學教育教學），2019（1）：55-62.

［2］丁曉丹.題組，提高數學解題能力的階梯［J］.小學教學研究，2021（21）：64-65，86.