源于教材的中考“圓”題

教材中的習題時常被修飾后，改頭換面變成我們的中考題。但在中考中，我們有可能因為識別不出它的原型，從而浪費很多時間。因此，我們在平時要多關注教材中的習題，特別是一些有價值的習題，可以以它們為母題，深度挖掘其價值，深入研究解題方法，發展思維的廣闊性和靈活性。比如，我們可以變換例題、習題的條件和結論，還可以一題多變，多題歸一。現以蘇科版數學八（上）第58頁的第10題為例，談談教材習題的重要性。

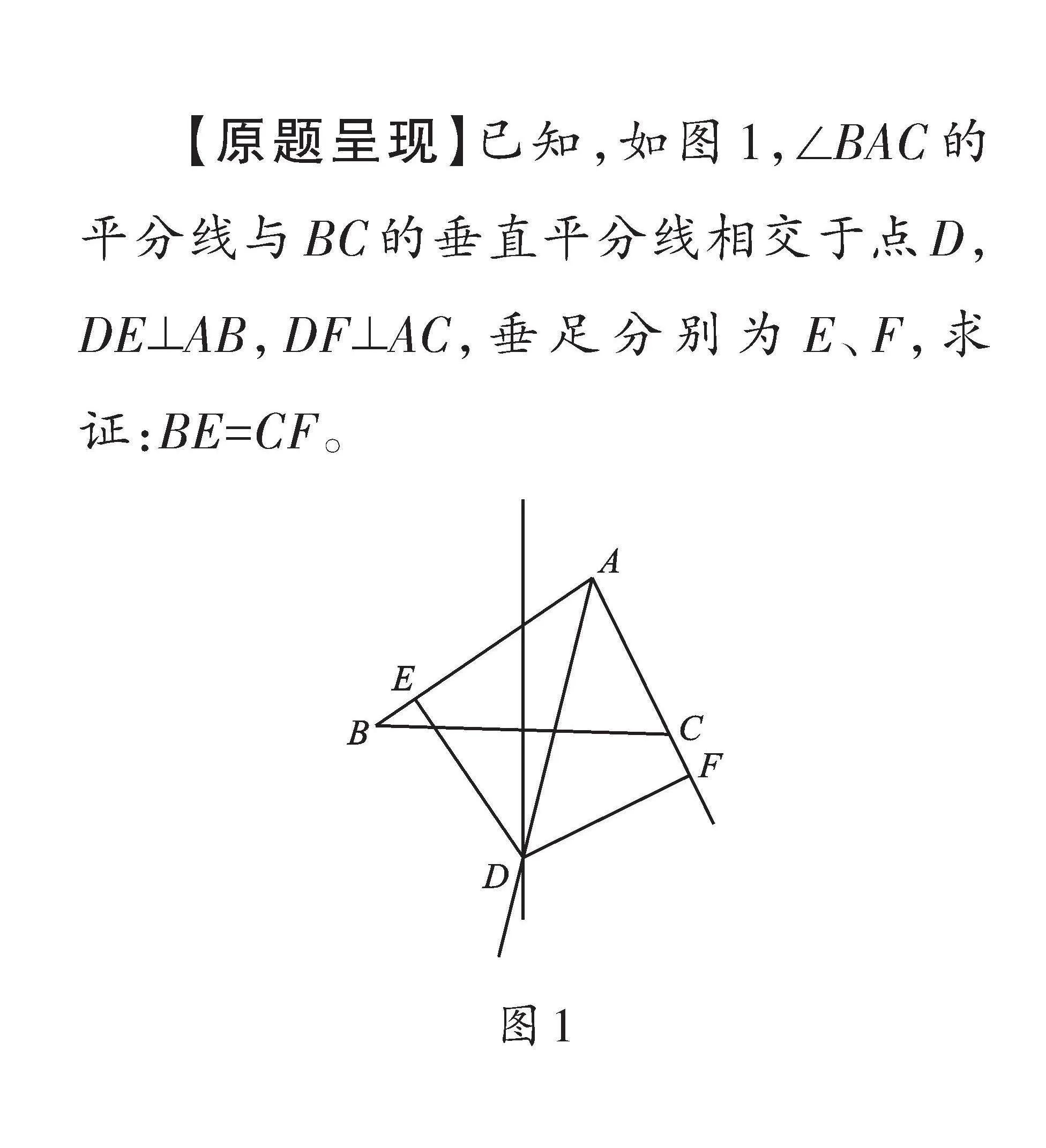
【原題呈現】已知，如圖1，∠BAC的平分線與BC的垂直平分線相交于點D，DE⊥AB，DF⊥AC，垂足分別為E、F，求證：BE=CF。

本題考查的是三角形全等部分的知識。要想證明兩條線段相等，從我們已有的經驗來看，可結合角平分線和垂直平分線的性質，聯想到利用三角形全等的知識來證明。

但是，我們做完之后，往往會忽略它的發展價值。其實，這是一道很好的母題。我們如果對它進行深度挖掘，將其與蘇科版數學九（上）圓的知識建立聯系，可以延伸出新的有價值的問題。

延伸 如圖2，BC為⊙O的直徑，A為BC上方⊙O上的一動點，∠BAC的平分線交⊙O于點D，DE⊥AB，DF⊥AC，垂足分別為E、F。

（1） 求證：BE=CF；

（2） 若CF=1，△ABC的面積為12，求AB的長。

本題在母題的基礎上添加了圓的背景。第（1）問還是通過構造全等來證明；第（2）問可以先證明四邊形DEAF是正方形，然后抓住△ABC的面積為12這個條件設未知數，列一元二次方程來解決。其實，我們還可以將第（2）問的條件弱化，思考AB、AC與AD的數量關系。我們不難發現，AB+AC=[2]AD。如果我們再將條件隱藏，就延伸出2023年江蘇省泰州市的數學中考第26題第（3）問。

已知：A、B為圓上兩定點，點C在該圓上，∠C為[AB]所對的圓周角。

（1）略。

（2）如圖3，若P為圓內一點，且∠APB＜120°，PA=PB，∠APB=2∠C。求證：P為該圓的圓心。

（3）如圖4，在（2）的條件下，若∠APB=90°，點C在⊙P位于直線AP上方部分的圓弧上運動。點D在⊙P上，滿足CD=[2]CB-CA的所有點D中，必有一個點的位置始終不變。請證明。

這時，我們不難發現，第（3）問就是對教材習題的進一步改編，通過隱藏條件、弱化條件、改變問法等方式，得到令人耳目一新的新內容。如果我們平時多注重思考，問題的解決豈不是手到擒來？因此，只要我們堅持這樣的思考，多問幾個為什么，就會對我們數學思維的提升有很大的幫助。

（作者單位：江蘇省泰州市姜堰區實驗初級中學）