基于Bezier曲線的圖形繪制技術的研究

摘要：針對現有繪圖軟件在對曲線圖形的繪制中，以拖動鼠標的方式改變曲線形狀的操作具有控制精度不高且軟件消耗資源大等缺點，本文在詳細推導貝塞爾（Bezier）曲線的描述方程后，根據其幾何特性提出了一種易于操控且資源消耗小的曲線圖形繪制方法。在圖形的繪制中，采用數學語言精確描述曲線的起止點、彎曲程度等特征，然后用曲線擬合的方式將圖形可視化地表現出來。運用這種方法，用戶可鍵入曲線關鍵參數，十分便捷地進行圖形設計、繪制等工作。

關鍵詞：Bezier曲線；圖形設計；直線擬合

一、引言

二維圖形在社會生產生活中的圖像顯示場景中占據著主導地位，這是由于二維圖像的直觀顯示能夠快捷、高效地傳遞信息。與三維圖像相比，二維圖像的生成和顯示成本顯著更低。觀察市場上的顯示設備，如電腦屏幕、電影院投影幕布、電子儀表盤等，它們所展示的內容都為二維圖像。二維圖像的廣泛使用也使得市場中有著大量的圖形設計需求，如品牌logo設計、電子宣傳牌圖形顯示設計等[1]。目前，市面上的圖形軟件種類繁多，其中廣泛使用的主要有支持高級圖像處理、深度應用于圖像編輯和設計領域的Adobe Photoshop，大量應用于矢量圖形設計和編輯的Adobe Illustrator等。這些繪圖軟件大多采用交互式的繪圖方案：用戶先用鼠標選取曲線、折線等繪圖模式，再拖動鼠標確定數個關鍵點，軟件根據繪圖模式將關鍵點用對應的連接方式相連。然而，要想用這樣的繪圖方式得到較為精美的圖形，較大程度上依賴于用戶對鼠標的控制能力和繪圖的熟練度。為了克服這一弊端，本文設計了一種基于數學語言描述的，能精確控制曲線的圖形繪制方法，用于更加精細地進行圖形設計和渲染。

二、曲線的描述與繪制

如何在計算機中繪制出一張二維圖像？對于任何一幅二維圖像，都可以將其分解為直線、曲線和填充色彩三部分。對于填充色彩，僅需要知道物體的輪廓，并在輪廓內進行相應的顏色填充，便能夠完成；對于直線的繪制，需要向計算機提供直線的起點坐標和終點坐標的數據，計算機將其連接后能產生特定的直線。如何繪制曲線？對于計算機而言，需要精確地知道待繪制曲線的描述函數才能實現繪制。本質上，直線的繪制也需要知道其數學函數，但僅需要簡單的一次函數即可；而曲線由于其靈活多變、復雜多樣的特點，對其進行一般性的數學描述會變得相對困難。能在計算機中近似描述曲線的方程有許多，其中性能最為優秀、使用最為廣泛的是Bezier曲線。Bezier曲線由法國數學家皮埃爾·貝塞爾于1962年提出，用于對二維和三維圖形的路徑和形狀進行數學描述[2]。由于其優秀的性能和簡潔的描述，Bezier曲線廣泛運用于多個圖像相關的領域。在圖形設計領域，主要用于圖標、字體的設計，較為有名和成功的應用是矢量圖形（SVG）、OpenType字體和Photoshop的曲線繪制等；在醫學圖像處理領域，用于邊緣曲線的提取和重建，具體有醫學圖像中的器官分割、細胞邊緣提取等；在游戲開發領域，用于創建人物的運動軌跡、粒子特效和曲線路徑等；在數值擬合和插值技術中，用于解決數值分析中的曲線擬合問題[3]。一言以蔽之，在眾多與曲線有關的場景中，Bezier曲線被廣泛使用，起到了不可或缺的作用。

三、Bezier曲線的數學描述

Bezier曲線是一種由起始點、控制點和結束點三個基本元素構成的幾何圖形。控制點數量越多，其能描述的曲線越復雜，一個二次Bezier曲線含有一個控制點，而一個三次Bezier曲線有兩個控制點，以此類推。隨著Bezier曲線的最高次數和控制點個數的增加，所描述曲線的自由度、復雜度和靈活性也相應增加，隨之使得Bezier曲線能夠更加精確地逼近目標曲線和路徑，但同時也會使得曲線的計算量和復雜度急劇增加。理論上，Bezier曲線的最高次數可以為任意正整數，但最為實用和常見的為二次和三次Bezier曲線，以下將對Bezier曲線方程進行詳細的推導。Bezier曲線由對若干條直線線性插值得到，一階Bezier曲線可由參數方程描述（1）表示為：

Pn （t） =P0+（P1 - P0） t （1）

式中，P0和P1為一階Bezier曲線的起始點和結束點；t為（0，1）區間內的常量；n表示Bezier曲線上點的序數；Pn （t） 為Bezier曲線上參數t的第n個坐標點。

圖1為一階Bezier曲線的示意圖，具體表現為一條直線段，可根據參數t的不同取值，依次計算得到Bezier曲線上的各點。

二次Bezier曲線由起始點P0、結束點P2和控制點P1插值得到，如圖2（a）所示，其中A為以P0和P1分別為起始點和結束點的一階Bezier曲線，B為以P1和P2分別為起始點和結束點的一階Bezier曲線，且滿足式（2）：

（2）

依次插值，求取滿足式（3）的Pn：

（3）

可由若干Pn點構成圖2（b）所示的P0到P2的二次Bezier曲線Pn，可由式（4）表示為：

Pn= （1-t） An+Bn （4）

其中，

An=（1-t） P0+ P1

Bn =（1-t） P1+ P2

代入式（4）后，Pn可由式（5）表示為：

Pn =（1-t）2 P0+2t（1-t）P1+t2 P2 （5）

其中t∈[0，1]。將t從0開始，按照一定步長依次取值可得到對應的一階Bezier曲線An和Bn的若干取值，然后對以A為起始點、以B為結束點的一階二次Bezier曲線以滿足線段AP與線段PB長度比值與AP0和AP1長度比值相同的條件，取得若干個Pn 點，由一階Bezier曲線得到的Pn 即為以P0和P2分別為起始點和結束點、以P1為控制點的二階Bezier曲線。將若干個Pn點平滑連接，則可得到圖2（b）所示的二階Bezier曲線。

按照上述邏輯，可相對容易地進一步推導出三階Bezier曲線。以A和D分別為起始點和終點，以B和C為兩個控制點的三階Bezier曲線可按照以下步驟得到：首先，求得分別以A和B為起始點和結束點的一階Bezier曲線E，以B和C分別為起始點和結束點的一階Bezier曲線F，和以C和D分別為起始點和結束點的一階Bezier曲線G；然后，繼續求取以E和F分別為起始點和結束點的一階Bezier曲線H，該一階Bezier曲線即為分別以A和C為起始點和結束點，以B為控制點的二階Bezier曲線；繼續求取以F和G分別為起始點和結束點的一階Bezier曲線I，該一階Bezier曲線即為以B和D為起始點和結束點、以C為控制點的二階Bezier曲線；進一步地，求取以H和I分別為起始點和結束點的一階Bezier曲線J，該一階Bezier曲線即為以E和G為起始點和結束點，以F為控制點的二階Bezier曲線，也即為以A和D分別為起始點和結束點，以B和C分別為兩個控制點的三階Bezier曲線。由此，便完成了三階Bezier曲線的推導。

用參數方程表示的Bezier曲線有其獨特的優勢，一是在于參數方程具有一定的形狀不變性和獨立性，其形式不受坐標系選取的影響；二是用切線的矢量形式表示其變化率，使得變化率具有有限性；三是以參數方程形式呈現的曲線具有較好的交互能力，能夠較為容易地實現旋轉、平移和縮放等幾何操作。

四、Bezier曲線的擬合與繪制

通過上文推導，可用確定的參數方程準確表示Bezier曲線。在計算機中要想利用參數方程進一步繪制和顯示Bezier曲線，一種較為簡便的方法是利用多段直線來擬合出曲線。以下將以二次Bezier曲線的擬合為例進行介紹。

對于式（5）的參數t，其取值范圍為區間[0，1]，將t在定義域內任意取值得到常數t1，將t1代入方程，可得到由P0和P2表示的Pn，并且P0和P2為二次Bezier曲線的起始點和結束點，其橫縱坐標是已知的，因此可計算得到t=t1時，Pn的橫縱坐標，由此便得到了位于Bezier曲線上的一個坐標點。然后t在區間[0，1]內任意取一個大于t1的值t2，將t2代入方程，可得到第二個Bezier曲線上的坐標點。按此方法不斷地將t取值為t3， t4，…，tn，可取得若干個位于曲線上的點。不難發現，當t取值的間隔值無限趨近于0時，可完整地獲取到該Bezier曲線上的所有點。但在實際的繪圖中，并不需要將曲線上的所有點都繪制出來，可采用多段短直線擬合多段短曲線，再將短直線依次首尾相連來近似地擬合曲線的方法。具體為，首先設置一個step參數，該參數的取值s表示將以P0和P1為起始點和結束點的Bezier曲線細分為數量為s的小段。將參數t依次取值1/step，2/step，3/step，…，然后將t依次代入二次Bezier曲線，可得到s個位于該曲線上的坐標點，最后將這些點用直線依次連接，便得到了Bezier曲線的近似繪圖。

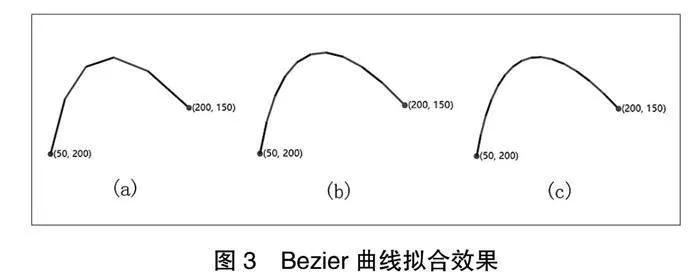
圖3 Bezier曲線擬合效果

圖3所示的（a）（b）（c）三幅子圖分別表示step取值為5、10、15時，Bezier曲線的擬合效果。由圖像可知，當step取值為5時，圖形有多處明顯不平滑的轉折點；當step取值為10時，圖形變得相對平滑，但依然能隱約看到輕微的轉折痕跡；當step取值為15時，曲線變得十分光滑。由此可見，不斷地增大step的值，能夠無限逼近二次Bezier曲線的真實圖形。

五、一種基于Bezier曲線的繪制方法

以上述技術為基礎，本文利用Bezier曲線設計了一種交互式的圖形繪制方法和對應的軟件程序。首先，由用戶設置所需要繪制的Bezier曲線的階數，并設定擬合段數n；其次，用戶在繪圖界面上按照起始點、控制點和結束點的順序依次用鼠標選取若干個點，將其作為初始的繪圖參數。軟件由鼠標交互事件獲取各選取點的坐標數據，并根據擬合段數求得每一子段的步長，將步長、起始點、控制點、結束點等數據代入對應階數的Bezier曲線方程即可計算得到將一條Bezier曲線拆分為n段后的子曲線的起始點和結束點坐標，將這些坐標點連接即可繪制出該Bezier曲線。軟件在獲取到用戶選取的關鍵點數據后，以SVG格式將這些數據存儲并顯示，而用戶在取得準確的坐標數據后，可通過鍵入坐標點的方式修改起始點、控制點、結束點的坐標以滿足實際的設計需求。在SVG文件中，通過簡易的參數修改即可個性化地繪制出精美的Bezier曲線，對曲線的外觀修改并不需要復雜的編程技能，而僅需要對相應的屬性值進行簡單的調整和修改即可。例如，修改“stroke： rgb”屬性所對應的值可設置曲線顏色，修改“stroke-width”屬性所對應的值可設置曲線寬度等。SVG圖形渲染簡單，用瀏覽器打開即可顯示對應的圖形，并且具有良好的矢量特性和內存占用小、兼容性強等優點，將設計完成的圖形保存為SVG文件能夠使得圖形便于修改和進一步的優化，并可借助SVG的繪圖特性對曲線進行精細化設計。該繪圖方法同時也保留鼠標交互式的曲線繪制模式，在用鼠標選取Bezier曲線的起始點、結束點和若干個控制點后，可進一步地用鼠標移動這些關鍵點，軟件自動記錄被移動后關鍵點的位置，更新至SVG文件中并渲染圖形，以便讓用戶直觀地看見改變關鍵點位置后圖形的顯示效果。

一種自適應擬合段數的求取方法。前文所描述的曲線繪制方法中以默認步長將Bezier曲線由多段直線擬合，而對于Bezier曲線的擬合段數這一參數，如果設置過小，會造成曲線分段明顯、弧線在繪制中不夠圓滑而影響顯示效果；但如果該值設置過大，則會由于計算量的突增而降低曲線繪制速度，影響軟件性能，合理設置擬合段數顯得十分重要。本文提出的繪圖方法中設計了一種基于曲線長度的擬合段數自適應求取方法，用于向用戶提供一個相對合理的擬合段數默認值。在Bezier曲線的繪制過程中曲線越長、彎曲程度越大，則平滑地繪制Bezier曲線需要的擬合段數就越多，因此需要得到待繪制Bezier曲線的長度和彎曲程度的信息。對于Bezier曲線的長度，計算方法具體為：首先將參數t從0開始，每間隔0.05依次取值并代入曲線方程，可得到該曲線上20個點的坐標信息，接著將相鄰的兩點用距離公式分別計算間距，最后分段累加即可得到該Bezier曲線長度的近似值。大量實驗結果表明，在Bezier曲線上每間隔15像素距離進行一次分段擬合能夠使得曲線擁有較好的顯示效果，因此將曲線長度與上述間隔像素距離的比值作為Bezier曲線的擬合段數。然后依照擬合段數依次求得Bezier曲線上對應的像素點，并分別計算其一階導數和二階導數后，進一步求取其曲率。如果該點的曲率大于一定閾值，則將該點與下一個分隔點之間增加一個分隔點，最后由曲線長度與間隔像素距離的比值加上增加的分隔點數即為推薦的擬合段數。

六、結束語

本文利用Bezier曲線提出了一種圖形繪制方法，能夠讓用戶通過鼠標與屏幕交互的方式選取關鍵點，然后由軟件自動地繪制出對應的Bezier曲線。相較于常規的繪圖軟件，本文設計的繪圖方法的優勢在于，一方面，能夠用量化的坐標精確地設計曲線圖形；另一方面，保留了交互式的繪圖方式，使其具有精確性的同時又不失靈活性。此外，該方法設計出的曲線采用矢量圖的形式保存，在對圖形進行修改、打印、顯示時，無論是將圖形進行放大、縮小還是旋轉等操作，圖形都能保持原有清晰度而不失真。

作者單位：馬秀紅 宋麗娟 德州市無線電檢測中心；黃守麗 成都大公博創信息技術有限公司

參考文獻

[1]周寅飛，張立華，賈帥東，等.最大可航窗口序列約束貝塞爾曲線的無人船自主航行航線規劃方法[J].武漢大學學報（信息科學版），2023：1-13.

[2]謝春麗，高勝寒，孫學志.融合改進A～*算法和Bezier曲線優化的路徑規劃算法[J].重慶理工大學學報（自然科學），2022，36（07）：177-187.

[3]楊洋，溫興，馬強龍，等.基于Bezier曲線的動態識別區農機避障路徑實時規劃[J].農業工程學報， 2022，38（06）：34-43.