“MPCK”視角下的高中數(shù)學(xué)問(wèn)題探究課堂

【摘 要】“MPCK”關(guān)注教師如何將數(shù)學(xué)知識(shí)的學(xué)術(shù)形態(tài)轉(zhuǎn)化為教育形態(tài)。現(xiàn)實(shí)中，MK、PK、CK在數(shù)學(xué)教育中已經(jīng)引起了廣大教師的關(guān)注，但TK的推廣和普及卻遠(yuǎn)遠(yuǎn)沒(méi)有達(dá)到預(yù)期。在高中數(shù)學(xué)教學(xué)中，教師可以借助GeoGebra軟件，通過(guò)掌握TK，為技術(shù)應(yīng)用提供保障；深化MK，為技術(shù)使用保駕護(hù)航；優(yōu)化PK，為技術(shù)呈現(xiàn)把控深淺；理解CK，為技術(shù)賦能精準(zhǔn)實(shí)施等措施，實(shí)現(xiàn)信息技術(shù)與教學(xué)的融合。

【關(guān)鍵詞】高中數(shù)學(xué)；MPCK；信息技術(shù)；GeoGebra；問(wèn)題探究

【中圖分類號(hào)】G633.6 【文獻(xiàn)標(biāo)志碼】A 【文章編號(hào)】1005-6009（2024）23-0061-06

【作者簡(jiǎn)介】楊磊，江蘇省溧陽(yáng)市教師發(fā)展中心（江蘇溧陽(yáng)，213300）高中數(shù)學(xué)研訓(xùn)員，高級(jí)教師。

MPCK是由數(shù)學(xué)學(xué)科知識(shí)（Mathematics Knowledge，簡(jiǎn)稱MK）、一般教學(xué)法知識(shí)（Pedagogical Knowledge，簡(jiǎn)稱PK）、關(guān)于學(xué)生的知識(shí)（Content Knowledge，簡(jiǎn)稱 CK）和關(guān)于教育技術(shù)的知識(shí)（Technical Knowledge，簡(jiǎn)稱TK）融合而成，其本質(zhì)是教師如何將數(shù)學(xué)知識(shí)的學(xué)術(shù)形態(tài)轉(zhuǎn)化為教育形態(tài)，以促進(jìn)學(xué)生的數(shù)學(xué)理解、提高學(xué)生的數(shù)學(xué)能力和提升學(xué)生的數(shù)學(xué)素養(yǎng)。［1］最初提出的MPCK并不包括TK，但隨著社會(huì)信息化的高速發(fā)展，信息技術(shù)對(duì)教育教學(xué)的影響越來(lái)越凸顯，TK及其與MK、PK、CK的有效融合受到越來(lái)越多的重視。《普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)（2017年版2020年修訂）》（以下簡(jiǎn)稱“新課標(biāo)”）提出，要注重信息技術(shù)與數(shù)學(xué)課程的深度融合，實(shí)現(xiàn)教學(xué)的實(shí)效性。［2］ 章建躍博士提出的四個(gè)理解：理解數(shù)學(xué)、理解教學(xué)、理解學(xué)生、理解技術(shù)［3］，也與MPCK不謀而合。

MK、PK、CK在數(shù)學(xué)教育中已經(jīng)引起了廣泛共鳴和重視，但TK的推廣和普及卻遠(yuǎn)遠(yuǎn)沒(méi)有達(dá)到預(yù)期。有些數(shù)學(xué)教師只會(huì)使用現(xiàn)成的PPT，并未掌握能夠匹配當(dāng)前教學(xué)的現(xiàn)代教育技術(shù)知識(shí)。本文以2021年全國(guó)高考甲卷（理科）第19題為例，用GeoGebra數(shù)學(xué)軟件（以下簡(jiǎn)稱“GGB”）開(kāi)展數(shù)學(xué)探究教學(xué)。在此過(guò)程中，除了呈現(xiàn)GGB技術(shù)知識(shí)，更重要的是展示TK在試題探究中的作用，給出基于MK、PK、CK的TK應(yīng)用思考。

一、問(wèn)題初探

1.試題呈現(xiàn)

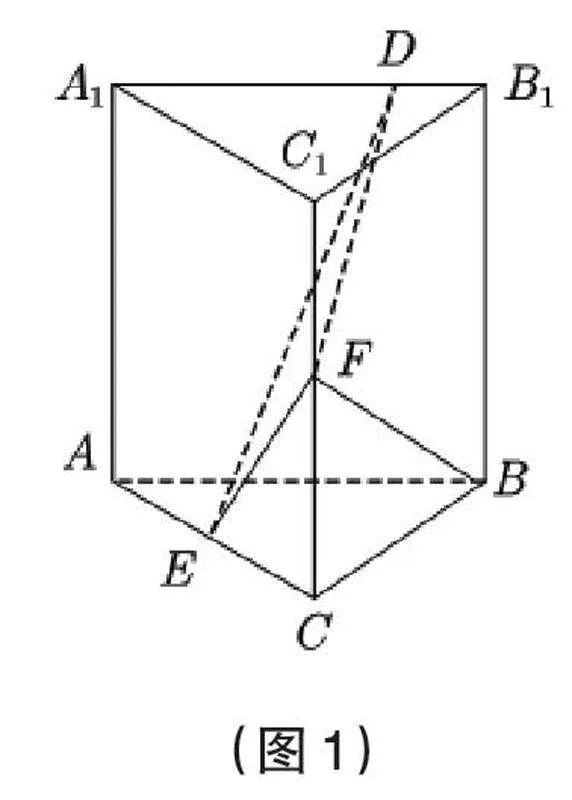
如圖1，已知直三棱柱ABC-A1B1C1中，側(cè)面AA1B1B為正方形，AB = BC = 2，E，F(xiàn)分別為AC和CC1中點(diǎn)，D為棱A1B1上的點(diǎn)，BF ⊥ A1B1。

（1）證明：BF ⊥ DE；

（2）當(dāng)B1D為何值時(shí)，面BB1C1C與面DFE所成的二面角的正弦值最小？

2.試題分析

這道立體幾何高考題，看似常規(guī)，卻有著豐富的內(nèi)涵，對(duì)不同學(xué)習(xí)層次的學(xué)生，都可以從中設(shè)計(jì)出有針對(duì)性的討論話題，具有較好的探究?jī)r(jià)值。其中，問(wèn)（1）已有文章作了詳細(xì)的分析探討［4］，本文主要針對(duì)問(wèn)（2）展開(kāi)。解決問(wèn)（2）的常規(guī)方法有向量坐標(biāo)法和綜合幾何法。向量坐標(biāo)法通過(guò)建立空間直角坐標(biāo)系，將問(wèn)題轉(zhuǎn)化為坐標(biāo)運(yùn)算，對(duì)邏輯思維要求較低，但需要一定的代數(shù)運(yùn)算能力。綜合幾何法聚焦直觀想象、邏輯推理、數(shù)學(xué)運(yùn)算等數(shù)學(xué)學(xué)科核心素養(yǎng)，需要學(xué)生具備空間想象和轉(zhuǎn)化化歸的能力。為了體現(xiàn)探究?jī)r(jià)值，提升學(xué)生的思維品質(zhì)，在此選擇用綜合幾何法分析解決，思路如下：

取BC中點(diǎn)G，連接B1G。設(shè)平面BCC1B [∩]平面DEF = l，過(guò)E作EH ⊥ l（H為垂足），連接GH，易證∠EHG即為二面角E-l-B的平面角，且sin∠EHG = [EGEH]，又由EG = 1知當(dāng)EH最大時(shí)，sin∠EHG最小。由EH ⊥ l知，EH≤EF（當(dāng)且僅當(dāng)F，H重合時(shí)取等號(hào)）。之后，在EF ⊥ l條件下求B1D的值。

二、融合方向

乍看題目，可能覺(jué)得沒(méi)有太大的必要運(yùn)用TK進(jìn)行探究。事實(shí)上，站在學(xué)生的角度，立體幾何題的難易程度很難一概而論。以空間想象能力為例，學(xué)生之間的差異很明顯，有些學(xué)生能夠輕易進(jìn)行數(shù)與形的轉(zhuǎn)換，想象出相關(guān)圖形。而對(duì)有些學(xué)生來(lái)說(shuō)，怎樣看圖都“不順眼”，總覺(jué)得數(shù)與形是分離的、“對(duì)不上號(hào)”。教師借助GGB的3D繪圖功能，將圖形繪制出來(lái)，進(jìn)行全方位的觀察感知，有利于培養(yǎng)學(xué)生的直觀想象能力，為分析和解決問(wèn)題作基礎(chǔ)性的鋪墊。 用GGB軟件協(xié)助尋找解題方向、進(jìn)行深入探究，主要圍繞以下幾點(diǎn)進(jìn)行：

（1）用GGB作出基本圖形，通過(guò)直觀感知和動(dòng)手操作確認(rèn)幾何體中各元素間的位置關(guān)系；

（2）用GGB求出面BCC1B1與面DEF的二面角，讓學(xué)生觀察并歸納其正弦值與線段B1D長(zhǎng)度之間的函數(shù)關(guān)系，感受其動(dòng)態(tài)關(guān)聯(lián)性；

（3）用GGB作出面BCC1B1與面DEF的二面角，尋找變化規(guī)律，梳理邏輯證明方案；

（4）尋找“圖根”和“題源”，并用GGB協(xié)助分析論證。

三、教學(xué)過(guò)程

1.作圖直觀感知

解決立體幾何問(wèn)題，首先要建立空間直觀，數(shù)形結(jié)合進(jìn)行分析。利用GGB軟件的3D繪圖功能，可以快速得到題目中的立體圖形：

S1：打開(kāi)3D繪圖區(qū)，依次輸入指令“A = （-sqrt（2），0，0）”“B = （0，sqrt（2），0）”“C = （sqrt（2），0，0）”“A_1 = A + （0，0，2）”“B_1 = B + （0，0，2）”“C_1 = C + （0，0，2）”，得到直三棱柱ABC-A1B1C1的六個(gè)頂點(diǎn)。

S2：輸入指令“棱柱（A，B，C，A_1）”，得到直三棱柱ABC-A1B1C1（名稱為a）。

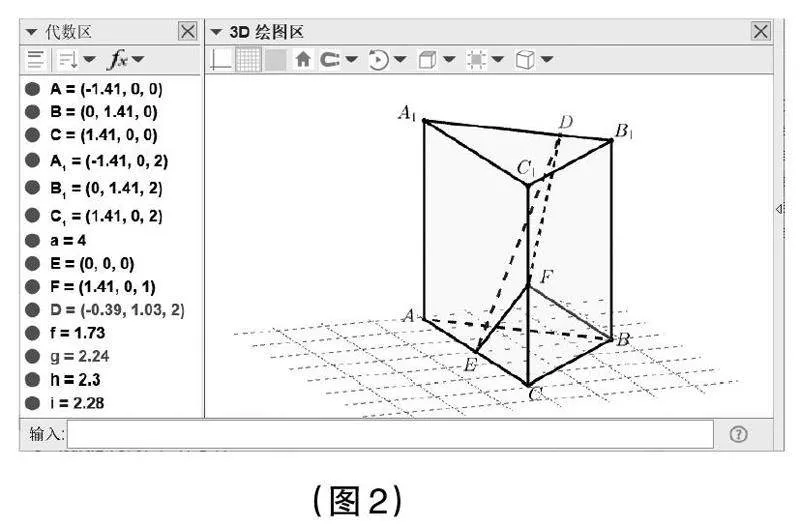
S3：用“描點(diǎn)”工具在線段A1B1上描出點(diǎn)D，用“中點(diǎn)”工具分別得到線段AC，CC1的中點(diǎn)E，F(xiàn)，再用“線段”工具連接EF，F(xiàn)B，DF，DE。還可以根據(jù)需要調(diào)整各個(gè)幾何對(duì)象的顏色、線徑等，得到與題目中相同的立體圖形。（見(jiàn)圖2）

課堂上，教師將光標(biāo)放在3D繪圖區(qū)內(nèi)，按住左鍵（或右鍵）移動(dòng)光標(biāo)，即可讓學(xué)生從各個(gè)方向觀察，進(jìn)一步直觀感知構(gòu)成幾何體的各要素之間的關(guān)系。

2.用軟件探最值

線段B1D長(zhǎng)度的變化引起了面BCC1B1與面DEF所成二面角α的變化，由此可以建立相關(guān)函數(shù)關(guān)系，用GGB軟件演示并感知其關(guān)聯(lián)性。下面，筆者利用GGB軟件的繪圖區(qū)，呈現(xiàn)二面角α關(guān)于線段B1D長(zhǎng)度的函數(shù)圖象，操作過(guò)程 如下：

S1：接圖2過(guò)程，輸入指令“線段（B_1，D）”，得到線段n。

S2：輸入指令“角度（平面（E，F(xiàn)，D），平面（C_1，B，C））”，得到二面角α。

S3：輸入指令“sin（α）”，得到α的正弦值b。

S4：輸入指令“P：（n，b）”，得到以線段B1D的長(zhǎng)度為橫坐標(biāo)、以二面角α的大小為縱坐標(biāo)的動(dòng)點(diǎn)P。

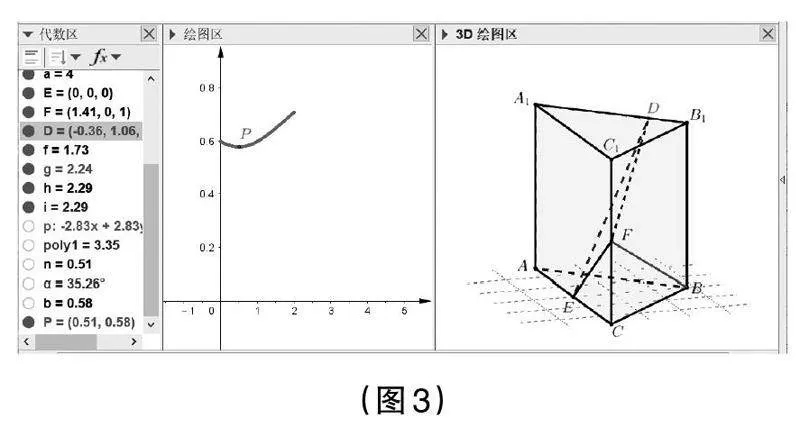
S5：打開(kāi)繪圖區(qū)，設(shè)置除點(diǎn)P外的其他對(duì)象在繪圖區(qū)中不可見(jiàn)。選中P點(diǎn)，單擊右鍵，選擇“開(kāi)啟跟蹤”，然后用鼠標(biāo)左鍵拖動(dòng)點(diǎn)D，即可在繪圖區(qū)中觀察到點(diǎn)P的變化。（見(jiàn)圖3）

如果時(shí)間充裕，上述過(guò)程完全可以當(dāng)堂操作完成，以便讓學(xué)生“看見(jiàn)”兩個(gè)變量的函數(shù)關(guān)系，明確邏輯論證的計(jì)劃：將兩個(gè)平面所成角的正弦值表示為線段B1D長(zhǎng)度的函數(shù)關(guān)系，再用代數(shù)知識(shí)分析求得函數(shù)最值。

3.看見(jiàn)“無(wú)棱”

平面BCC1B1與平面DEF所成二面角在哪里？直觀呈現(xiàn)這個(gè)二面角的平面角，有助于學(xué)生展開(kāi)邏輯思維，學(xué)會(huì)運(yùn)用綜合法分析問(wèn)題，怎樣呈現(xiàn)相關(guān)的二面角呢？具體操作如下：

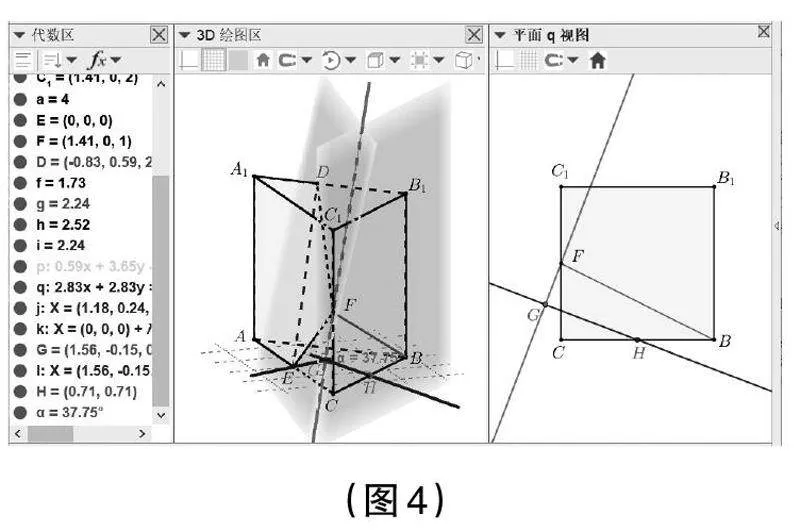
S1：接圖2過(guò)程，用“三點(diǎn)共面”工具依次選中點(diǎn)D，E，F(xiàn)，得到平面p，再選中點(diǎn)B，C，C1，得到平面q。用“相交曲線”指令得到平面p和q的交線j。用“垂線”工具，依次選中E，j，得到過(guò)點(diǎn)E且與直線j垂直的直線k，再用“交點(diǎn)”工具得到j(luò)與k的交點(diǎn)G。

S2：選中平面q，右鍵單擊，選中“創(chuàng)建q的平面視圖”，并在此視圖中用“垂線”工具得到過(guò)G點(diǎn)與j垂直的直線l，用“交點(diǎn)”工具得到l與線段BC的交點(diǎn)H。由此，相關(guān)平面角構(gòu)造完成（即為直線EG和GH所成角）。（見(jiàn)下頁(yè)圖4）

S3：輸入指令“角度（E，G，H）”，即可在代數(shù)區(qū)顯示∠EGH的值。鼠標(biāo)拖動(dòng)點(diǎn)D，觀察相關(guān)幾何對(duì)象及∠EGH的度數(shù)變化，可以發(fā)現(xiàn)點(diǎn)H始終在線段BC的中點(diǎn)位置，且當(dāng)G點(diǎn)與F點(diǎn)重合時(shí)，∠EGH最小。

教師可以借由上述操作感知的結(jié)論發(fā)問(wèn)，將學(xué)生思維引向深入。經(jīng)由充分的思考和討論，不難得知：之所以點(diǎn)H始終在線段BC的中點(diǎn)位置，是因?yàn)镋H⊥平面BCC1B1。此時(shí)，根據(jù)學(xué)生情況，教師可考慮適當(dāng)引入或回顧“三垂線定理”以便加深學(xué)生對(duì)問(wèn)題的理解。又在RtΔEGH中，sin[∠EGH] = [EHEG] = [1EG]，又EG≤EF（點(diǎn)G與點(diǎn)F重合時(shí)取等號(hào)），由此可知點(diǎn)G與點(diǎn)F重合時(shí)∠EGH最小。

當(dāng)點(diǎn)G與點(diǎn)F重合時(shí)，BF與二面角的棱垂直，在平面BCC1B1中，利用平面幾何知識(shí)不難得出棱線過(guò)線段B1C1的中點(diǎn)M。假設(shè)EF [∩] A1C1 = N，則A1C1 = 2C1N，且D，M，N共線。在平面A1B1C1中，過(guò)C1作A1B1的平行線（交直線MN于點(diǎn)T），利用ΔDB1M～ΔTC1M及ΔA1ND～ΔC1NT，可得B1D = 1。（見(jiàn)圖5）

4.尋找“圖根”

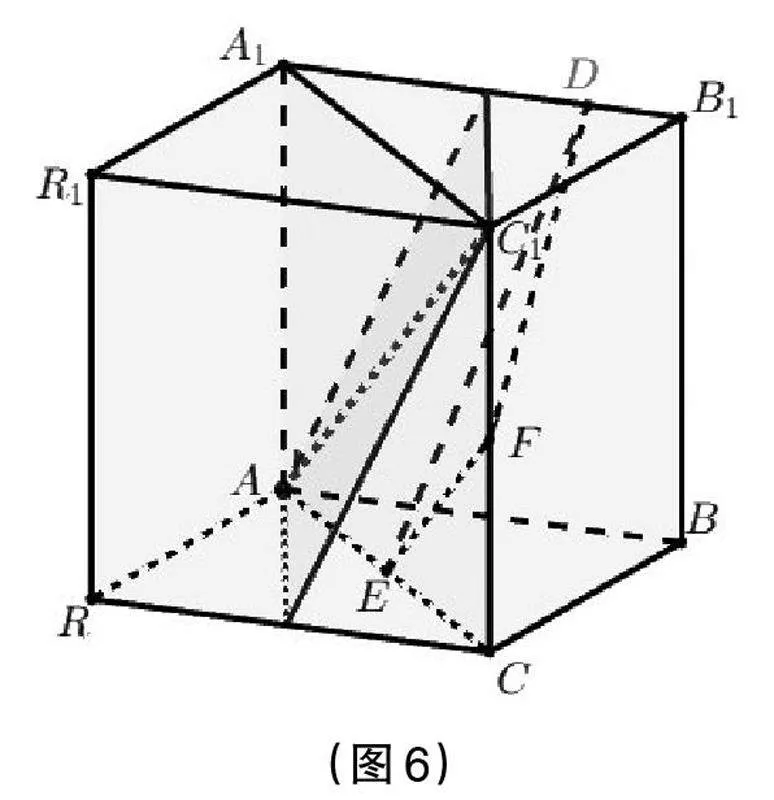
題目所給的直三棱柱是一個(gè)“塹堵”模型（底面為直角三角形的直棱柱），可以補(bǔ)成正方體ABCR-A1B1C1R1。這種補(bǔ)形成常規(guī)幾何的想法和視角，有利于學(xué)生以聯(lián)系的眼光看待已有知識(shí)和問(wèn)題。GGB軟件操作如下：

接圖2過(guò)程，輸入指令“R：A + C - B”和“R_1：A_1 + C_1 - B_1”，得到點(diǎn)R，R1，再輸入指令“棱柱（A，C，R，A_1）”，即可補(bǔ)成所需正方體。（見(jiàn)圖6）

由題知AC1∥EF，過(guò)直線AC1作平面DEF的平行平面α，即可將平面DEF與平面BCC1B1所成角轉(zhuǎn)化為平面α與平面BCC1B1所成角。

轉(zhuǎn)化成最為常見(jiàn)的正方體模型，能夠增強(qiáng)學(xué)生的信心，幫助他們找到解題思路。這樣的分析探討有助于學(xué)生“居高臨下”看問(wèn)題，與此同時(shí)，學(xué)生也在進(jìn)行角色轉(zhuǎn)換，由做題者變成出題者。

5.“溯源”問(wèn)題

由條件知平面DEF始終圍繞EF旋轉(zhuǎn)，緊抓這個(gè)特征，剔除次要或無(wú)關(guān)因素，就可以思考下面更一般性的問(wèn)題：若直線AB為平面α的一條斜線，求過(guò)AB的平面β與α所成角的最小值。下面，借助GGB軟件進(jìn)行操作探究：

S1：打開(kāi)3D繪圖區(qū)，在樣式欄中調(diào)整出“xOy平面”，用“直線”工具作直線AB（A在xOy平面內(nèi)），用“垂線”工具過(guò)點(diǎn)B作xOy平面的垂線g，再用“交點(diǎn)”工具得到垂線g與xOy平面的交點(diǎn)C。

S2：打開(kāi)繪圖區(qū)，用“滑動(dòng)條”工具創(chuàng)建角度滑動(dòng)條α。

S3：輸入指令“旋轉(zhuǎn)（平面（A，B，C），α，f）”（f為直線AB），得到平面ABC圍繞直線AB旋轉(zhuǎn)α角度所得的平面p。

S4：用“相交曲線”工具得平面ABC與平面p的交線h，用“垂線”工具過(guò)點(diǎn)B作h的垂線i，用“交點(diǎn)”工具得h與i的交點(diǎn)D，再用“直線”工具連接C，D。

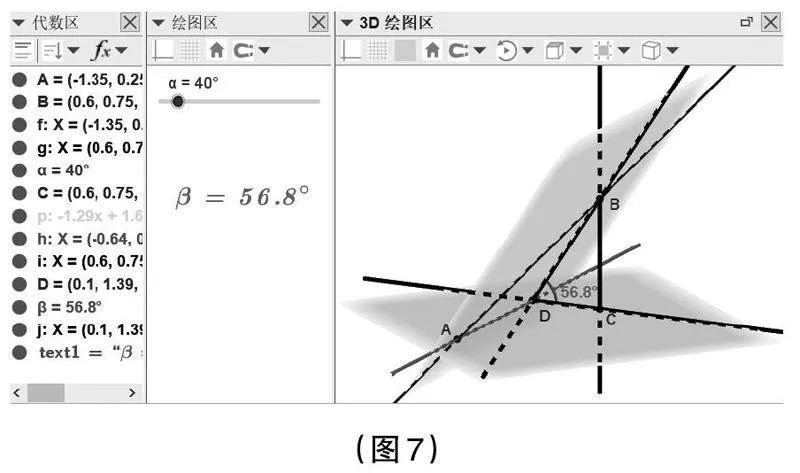
S5：輸入指令“角度（B，D，C）”，即可得到xOy平面與平面p的夾角β。（見(jiàn)圖7）

用鼠標(biāo)拖動(dòng)滑動(dòng)條α，觀察角度β的變化，會(huì)發(fā)現(xiàn)當(dāng)α = 90°時(shí)，角度β最小，此時(shí)點(diǎn)D與點(diǎn)A重合，由此可知感知一般性問(wèn)題的結(jié)論是：平面β與α所成角的最小值即為直線AB與平面α所成角。

四、教學(xué)反思

MPCK是MK，PK，CK和TK的融合，隨著教師教齡增加和經(jīng)驗(yàn)積累，每一種知識(shí)也會(huì)相應(yīng)增加，交集部分增多，融合之后，教師的“MPCK”也會(huì)相應(yīng)發(fā)展。［5］教師的MK，PK，CK和TK并不是孤立存在的，它們之間有著緊密的聯(lián)系，相互影響、相輔相成。下面，筆者著眼于教師的TK，站在技術(shù)融合的視角，作進(jìn)一步說(shuō)明。

1.掌握TK，為技術(shù)應(yīng)用提供保障

掌握TK，是應(yīng)用技術(shù)的前提。以GGB為例，教師若僅僅會(huì)簡(jiǎn)單的操作，拿別人的成品課件進(jìn)行展示，教學(xué)效果則非常有限。教師倘若能夠較好地掌握GGB的基本操作，就可以當(dāng)堂演示，或者引導(dǎo)學(xué)生動(dòng)手操作。當(dāng)堂演示往往能夠提供較好的學(xué)習(xí)代入感，展示動(dòng)態(tài)生成的過(guò)程，提升學(xué)生的投入度；教學(xué)生自己動(dòng)手操作，積極調(diào)動(dòng)學(xué)生所有感官參與學(xué)習(xí)，能夠增加學(xué)生的活動(dòng)經(jīng)驗(yàn)，更好地使學(xué)生集中思維、激發(fā)靈感、快速突破。

在上述的試題探究中，如果條件允許，教師可以讓學(xué)生操作GGB軟件，親自動(dòng)手繪制二面角的平面角，拖動(dòng)動(dòng)點(diǎn)D，觀察二面角大小的變化……將探索工具交到學(xué)生手中，讓學(xué)生在做中學(xué)、學(xué)中悟，有利于提升學(xué)生的學(xué)習(xí)興趣，激發(fā)其可持續(xù)性發(fā)展的潛能。

另外，TK的掌握不是一蹴而就的，需要長(zhǎng)時(shí)間的學(xué)習(xí)和實(shí)踐。以GGB為例，從入門到精通，可能需要幾個(gè)月甚至幾年的時(shí)間。為了實(shí)現(xiàn)較好的教學(xué)效果、提升教學(xué)的實(shí)效性，教師需要投入一定的時(shí)間與精力進(jìn)行相關(guān)技術(shù)的學(xué)習(xí)。

2.深化MK，為技術(shù)使用保駕護(hù)航

數(shù)學(xué)軟件的設(shè)計(jì)和操作本身就是以MK為根基。以GGB軟件為例，它的開(kāi)發(fā)除了必要的計(jì)算機(jī)知識(shí)和硬件條件，最重要且基礎(chǔ)的是相關(guān)數(shù)學(xué)知識(shí)。它的工具和指令的設(shè)計(jì)均包含相應(yīng)的數(shù)學(xué)原理，如“直線”工具源自“兩點(diǎn)確定一條直線”，“平行直線”工具源自“過(guò)一點(diǎn)有且只有一條直線與已知直線平行”，“三點(diǎn)平面”工具源自“不在同一直線的三點(diǎn)確定一個(gè)平面”，“橢圓”工具源自“兩焦點(diǎn)和一定點(diǎn)可確定一個(gè)橢圓”，“對(duì)稱”指令源自相關(guān)的對(duì)稱原理……如果用GGB作圓柱圓錐的展開(kāi)圖，需要掌握參數(shù)方程的相關(guān)知識(shí)；想要靈活運(yùn)用“曲線”“曲面”等指令，簡(jiǎn)化作圖過(guò)程，需要掌握“點(diǎn)運(yùn)算”，理解向量、直角坐標(biāo)點(diǎn)、極坐標(biāo)點(diǎn)、復(fù)數(shù)之間的聯(lián)系。

另外，MK中蘊(yùn)含的數(shù)學(xué)觀念、數(shù)學(xué)思想方法、數(shù)學(xué)史等，也為教師應(yīng)用TK提供了重要的參考依據(jù)和標(biāo)準(zhǔn)。

3.優(yōu)化PK，為技術(shù)呈現(xiàn)把控深淺

教師PK蘊(yùn)含的教育理念、教育理論知識(shí)、課程知識(shí)、教學(xué)知識(shí)等，對(duì)教師TK“是否要使用”“如何使用”“何時(shí)使用”“使用到什么程度”等影響較大。

教師要不斷更新教育理念，不能故步自封，要勇于嘗試。如果教師本身缺乏探索精神和對(duì)教學(xué)的深度理解，認(rèn)為是否使用TK、何時(shí)使用TK無(wú)關(guān)緊要，就不會(huì)有較理想且恰當(dāng)?shù)募夹g(shù)呈現(xiàn)。“教是為了不教”，教學(xué)是為了培養(yǎng)可持續(xù)發(fā)展的自立自強(qiáng)的人，教師不能局限于暫時(shí)的顯性成績(jī)，更要注重促進(jìn)可持續(xù)發(fā)展的隱性能力和品質(zhì)的培養(yǎng)。

如上述采用GGB軟件實(shí)施教學(xué)，協(xié)助學(xué)生分析探討問(wèn)題，就要基于PK設(shè)計(jì)，以增強(qiáng)學(xué)生的直觀感知和空間想象，激發(fā)學(xué)生的興趣和思維，提升學(xué)生分析和解決問(wèn)題的能力，培養(yǎng)學(xué)生提出和發(fā)現(xiàn)問(wèn)題的意識(shí)，讓學(xué)習(xí)變得更加主動(dòng)和高效。

教師應(yīng)優(yōu)化自己的PK，明確適合使用信息技術(shù)的環(huán)境（驗(yàn)證、探索、實(shí)驗(yàn)、觀察等），才能助力學(xué)生有所發(fā)現(xiàn)和感悟，促進(jìn)學(xué)生高階思維的生成，實(shí)現(xiàn)學(xué)科育人。

4.理解CK，為技術(shù)賦能精準(zhǔn)實(shí)施

不理解學(xué)生，就是不理解教vJ9hTjmAVMYWM3H5tvcfug==學(xué)。理解CK，是實(shí)施有效教學(xué)的前提。不同于教師獨(dú)立的數(shù)學(xué)研究，引導(dǎo)學(xué)生進(jìn)行問(wèn)題探究必須關(guān)注學(xué)生的知識(shí)水平、認(rèn)知發(fā)展水平、學(xué)習(xí)環(huán)境等。上述案例中，倘若學(xué)生連最基本的空間向量法都沒(méi)有較好掌握，或者用綜合法解題的基礎(chǔ)非常薄弱，我們就要考慮是否真的有必要利用信息技術(shù)進(jìn)行深度探究。認(rèn)準(zhǔn)了CK，才能實(shí)現(xiàn)精準(zhǔn)的技術(shù)賦能。

理解CK，要求教師充分了解學(xué)情，明晰教學(xué)目標(biāo)，對(duì)問(wèn)題探究的深度做到心中有數(shù)。比如在上述探究中，向量投影法、三垂線定理、“塹堵”模型、三余弦定理等都可以與問(wèn)題相關(guān)聯(lián)，并且用GGB協(xié)助探究。需不需要這樣做要根據(jù)具體的學(xué)情而定，不能一概而論。 教師更不能為了“炫耀自己的技術(shù)”就帶領(lǐng)學(xué)生一直往深處探究。靠近最近發(fā)展區(qū)，“跳一跳能夠得著”，這些基本的教學(xué)原則教師要把握住。

【參考文獻(xiàn)】

［1］李渺，寧連華.數(shù)學(xué)教學(xué)內(nèi)容知識(shí)（MPCK）的構(gòu)成成分表現(xiàn)形式及其意義［J］.數(shù)學(xué)教育學(xué)報(bào)，2011，20（2）：10-14.

［2］中華人民共和國(guó)教育部.普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)（2017年版2020年修訂）［S］.北京：人民教育出版社，2020：3.

［3］章建躍.核心素養(yǎng)立意的高中數(shù)學(xué)課程教材教法研究［M］.上海：華東師范大學(xué)出版社，2021：5.

［4］劉熙，劉冰楠.聚焦數(shù)學(xué)核心素養(yǎng) 引導(dǎo)立體幾何教學(xué)：以2021年高考數(shù)學(xué)全國(guó)甲卷文科第19題為例［J］.數(shù)學(xué)通報(bào)，2022，61（10）：51-57.

［5］陸明明.MPCK視角下“三角函數(shù)的周期性”的教學(xué)設(shè)計(jì)對(duì)比分析與建議［J］.數(shù)學(xué)通報(bào)，2015，54（2）：25-29.