“豬腳模型”在初中數學平行線相關題目中的應用


【摘要】隨著教育改革的深入,尋找更加生動、有趣的教學方法成為教育工作者關注的焦點.本文主要探討一種新的教學方法——豬腳模型在初中數學平行線相關題目中的應用.首先介紹豬腳模型的定義和基本原理,使得學生能夠更加直觀地理解平行線之間的角度關系.然后通過具體的例子和練習,展示豬腳模型在實際解題中的應用,并分析其對學生學習興趣和思維能力的影響.
【關鍵詞】初中數學;平行線;豬腳模型
1 引言
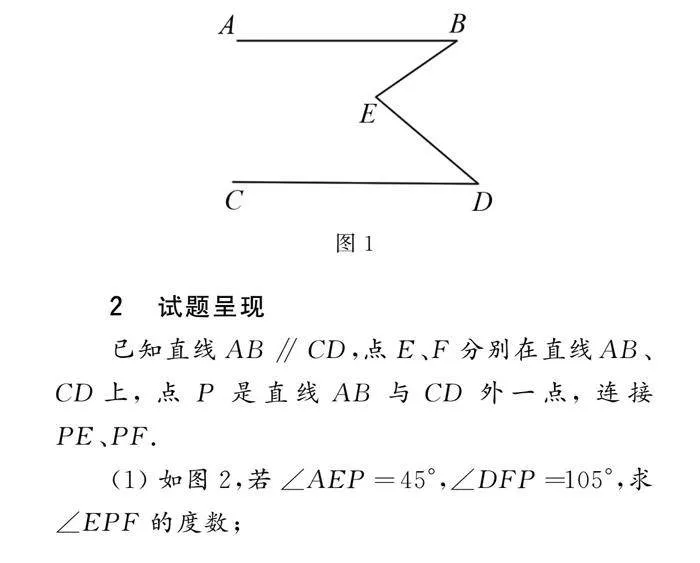
如圖1所示,若AB∥CD,則∠B+∠D=∠E.由于該圖外形像“豬腳”,因此這一定理被稱為“豬腳模型”.在初中數學的教學中,平行線的性質是一個重要的內容.在學習平行線的性質時,學生經常會遇到一些有關角度的問題.為了幫助學生更好地理解和解決這類問題,教師可以引入一個有趣且形象的模型——豬腳模型.通過運用豬腳模型,學生可以更加輕松地解決平行線相關題目.他們不再需要死記硬背公式,而是可以通過觀察和思考來找到答案.這種教學方法的引入,不僅提高了學生的學習興趣,也培養了他們的觀察力和思維能力.
2 試題呈現
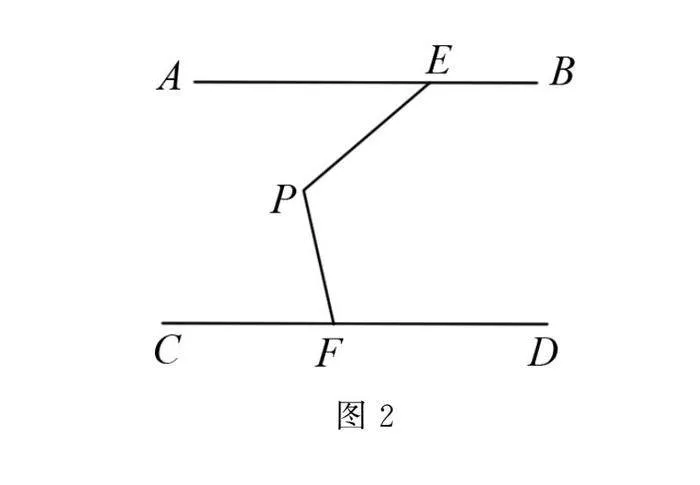
已知直線AB∥CD,點E、F分別在直線AB、CD上,點P是直線AB與CD外一點,連接PE、PF.
(1)如圖2,若∠AEP=45°,∠DFP=105°,求∠EPF的度數;
(2)如圖3,過點E作∠AEP的角平分線EM交FP的延長線于點M,∠DFP的角平分線FN交EM的反向延長線交于點N,若∠M與3∠N互補,試探索直線EP與直線FN的位置關系,并說明理由;
(3)若點P在直線AB的上方且不在直線EF上,作∠DFP的角平分線FN交∠AEP的角平分線EM所在直線于點N,請直接寫出∠EPF與∠ENF的數量關系.
3 思路分析
第一問為“豬腳模型”的證明,過P作PQ∥AB,根據平行線的性質可得∠EPF=120°,在解題過程中,如不需詳細步驟的題目,可直接應用;第二問根據角平分線的定義和三角形外角的性質可得結論;第三問根據角平分線的定義和平行線的性質分情況討論即可.
4 解題探究
(1)如圖4,過P作PQ∥AB,
因為AB∥CD,
所以PQ∥CD,
所以∠QPE=∠AEP=45°,∠QPF=∠180°-∠DFP=180°-105°=75°,
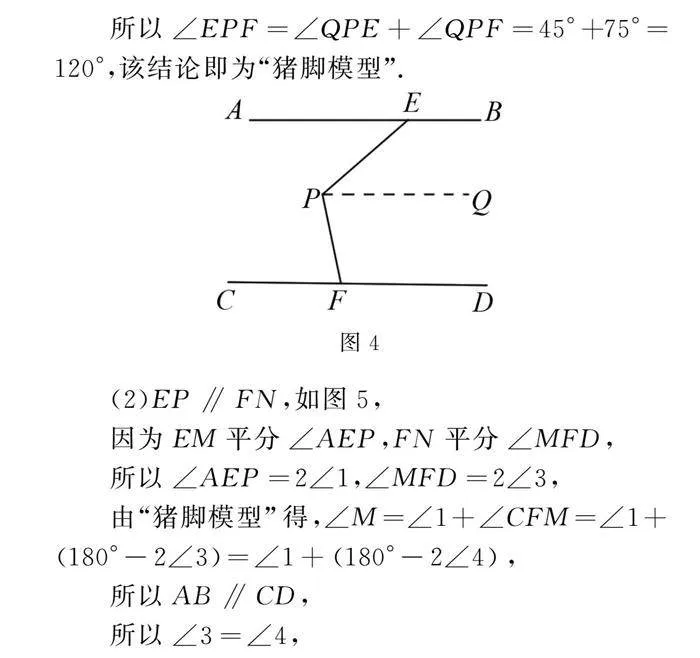
所以∠EPF=∠QPE+∠QPF=45°+75°=120°,該結論即為“豬腳模型”.
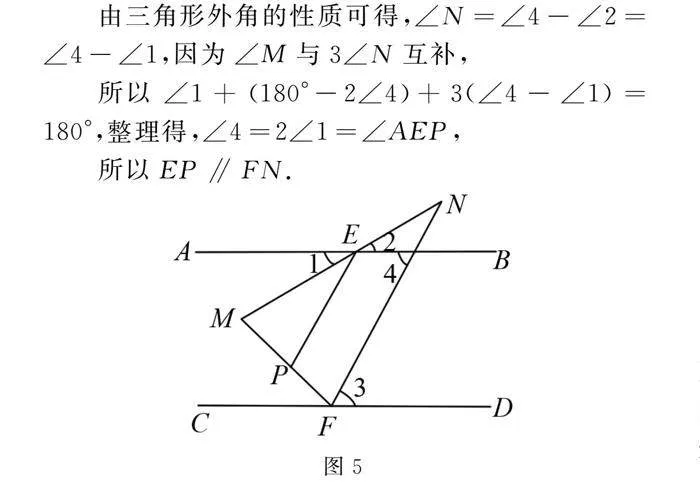
(2)EP∥FN,如圖5,
因為EM平分∠AEP,FN平分∠MFD,
所以∠AEP=2∠1,∠MFD=2∠3,
由“豬腳模型”得,∠M=∠1+∠CFM=∠1+180°-2∠3=∠1+180°-2∠4,
所以AB∥CD,
所以∠3=∠4,
由三角形外角的性質可得,∠N=∠4-∠2=∠4-∠1,因為∠M與3∠N互補,
所以∠1+180°-2∠4+3(∠4-∠1)=180°,
整理得,∠4=2∠1=∠AEP,
所以EP∥FN.
第二問中用到第一問“豬腳模型”的結論,由于本題存在第一問,因此可以直接運用,當題目中沒有第一問時,學生也應該鍛煉運用“豬腳模型”的敏感性.
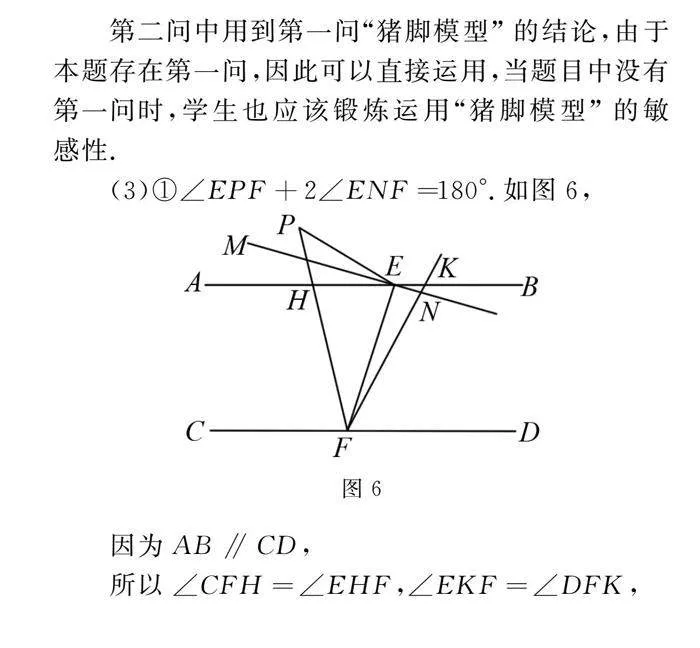
(3)①∠EPF+2∠ENF=180°.如圖6,
因為AB∥CD,
所以∠CFH=∠EHF,∠EKF=∠DFK,
因為FN平分∠DFP,ME平分∠AEP,
所以∠CFH=180°-2∠DFK,∠AEP=2∠AEM=2∠KEN,由外角的性質得,∠EPF=∠EHF-∠AEP=180°-2∠DFK-2∠AEM,∠ENF=∠EKF+∠KEN=∠DFK+∠AEM,
所以∠EPF=180°-2∠ENF,
所以∠EPF+2∠ENF=180°.
②∠EPF=2∠ENF-180°,如圖7,
因為AB∥CD,
所以∠PKB=∠PFD=2∠DFN,由外角的性質得,∠EPF=∠PKB-∠BEP=∠PKB-180°-2∠MEP=2∠DFN+2∠AEM-180°,
由“豬腳模型”得,∠ENF=∠DFN+∠NEK=∠DFN+∠AEM,
所以2∠ENF=2∠DFN+2∠AEM,
所以∠EPF=2∠ENF-180°.
5 結語
本題考查平行線判定和性質,角平分線的定義,三角形外角與內角的關系,根據題意理清各角之間的關系是解題關鍵.“豬腳模型”是平行線中的重要結論,需謹記其證明過程,并熟練運用.“豬腳模型”是一種有效的教學方法,它能夠幫助學生更好地理解和解決初中數學中平行線相關題目.通過引入“豬腳模型”,學生能夠更加直觀地理解平行線之間的角度關系,提高他們的學習興趣和思維能力.在教學過程中,教師可以通過舉例和練習來引導學生運用“豬腳模型”.解決相關數學問題.使學生
更好地掌握平行線的性質.
參考文獻:
[1]孫振飛,顧葉青.“平行線被折線所截問題”的探究:變式、開放、融合——兼談滬教版初中數學教材中探究活動的教學[J].數學教學,2023(12):16-22.
[2]欒長偉.巧添平行線 構造相似形[J].初中生學習指導,2023(33):20-22.
[3]陳國權.平行線間的“拐點”問題[J].中學教學參考,2023(23):22-24.

