初中數學翻折模型的中心條件與解題思路

【摘要】初中數學教學中,翻折模型作為幾何學習的重要內容之一,旨在培養學生的幾何思維和問題解決能力.本文以初中數學教學中的翻折模型為研究對象,探討了其解題過程中的中心條件與思路.研究發現,翻折模型的教學不僅僅是為了掌握具體的解題方法,更重要的是培養學生的空間想象能力、邏輯推理能力和問題解決能力.
【關鍵詞】初中數學;翻折模型;中心條件;解題思路
1 引言
初中數學作為學生學習的重要學科之一,在培養學生的邏輯思維和解決問題能力方面發揮著重要作用.其中,翻折模型作為數學教學中的一個重要內容,旨在通過幾何圖形的折疊和全等性質的運用,培養學生的空間想象能力和幾何推理能力[1].筆者將以一道例題進行探究,以“全等性”“對稱性”為該類題目中心條件和破題關鍵,以“根據全等性和已知條件確定所有已知量,設出未知量,在同一個圖形內構造等量關系,解出未知量”為該類題的一般解題思路,通過合理引導學生運用全等性質,提升學生的問題解決能力和數學思維水平.
2 翻折模型的概述
翻折變換,亦稱折疊問題,其本質是一種軸對稱變換.在幾何學中,折疊操作將圖形沿某一條直線(稱為折痕或對稱軸)進行翻折,使得折疊前后的圖形部分或全部重合.學生在解題過程中,需要時刻牢記翻折模型的具體性質,即:折疊前后圖形的形狀和大小保持不變,但位置會發生改變;折疊過程中,對應邊和對應角保持相等.這些性質為學生解決折疊問題提供了重要的理論依據.
在解決實際問題時,面對較為復雜的折疊問題,學生可以通過實際操作圖形的折疊來尋找圖形間的關系.這種方法有助于學生直觀地理解問題,從而找到解題的突破口.學生還需要明確折疊和軸對稱所能提供的隱含條件,并充分利用這些條件.通常,可以設要求的線段長度為x,然后根據折疊和軸對稱的性質,用含x的代數式表示其他相關線段的長度.然后選擇適當的直角三角形,運用勾股定理列出方程,進而求解出x的值.在運用方程解決問題時,學生應認真審題,確保設定的未知數正確無誤.同時,要注意分析題目中的已知條件和所求目標,將實際問題轉化為數學模型,再通過數學方法求解.在此過程中,熟練掌握折疊和軸對稱的性質,以及靈活運用勾股定理等幾何知識,是解決折疊問題的關鍵.總之,掌握折疊問題的解題方法,不僅有助于提高學生的幾何解題能力,還能培養學生的空間想象力和邏輯思維能力.
3 試題呈現
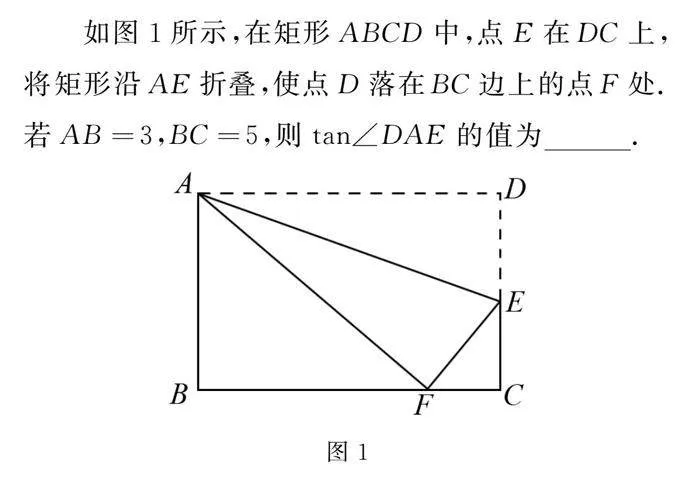
如圖1所示,在矩形ABCD中,點E在DC上,將矩形沿AE折疊,使點D落在BC邊上的點F處.若AB=3,BC=5,則tan∠DAE的值為________.
4 思路分析
本題運用倒推法,若需要求出tan∠DAE,由于已知BC=5,則可得到AD=5,故只需求解DE的長度即可.嘗試利用“根據全等性和已知條件確定所有已知量,設出未知量,在同一個圖形內構造等量關系,解出未知量”的一般解題思路進行求解.首先,根據全等性,可知AF=5,因此可求BF的長度,同時滿足全等性的還有EF=DE.設未知量為DE的長度x,則不難發現,在△CEF中,可以根據勾股定理進行等式構建,從而解出未知量.
而本題還可根據“對稱性”這一中心條件,進行簡化求解.可以連接D、F兩點,根據對稱性,可知對稱軸與連線垂直.因此根據相似三角形,可將tan∠DAE等價于tan∠FDE,如此一來,便不需要設未知量即可求解[2].
5 解題探究
解法1 一般思路
如圖1,由翻折變換可知,AD=AF=5,在Rt△ABF中,由勾股定理得BF=AF2-AB2=52-32=4,因此FC=BC-BF=5-4=1,設DE=x,則EF=x,EC=3-x.
在Rt△EFC中,由勾股定理得12+(3-x)2=x2,解得x=53,即DE=53,在Rt△ADE中,tan∠DAE=DEAD=535=13.
解法2 升階思路
如圖2,連接D、F兩點,交AE于點O,則根據對稱性,對稱兩點的連線垂直于翻轉軸,則AE⊥DF.由于∠ADE=∠DOE,∠AED=∠ADO,所以∠DAE=∠ODE,因此tan∠DAE=tan∠ODE=tan∠FDC,此時可根據解法1中結論得到FC=1,又因為CD=3,所以tan∠DAE=13.
6 解后反思
在本文的探討中,筆者深入研究了翻折模型在初中數學教學中的重要性和應用.翻折模型的教學不僅僅是為了讓學生掌握具體的解題方法,更重要的是培養學生的空間想象能力、邏輯推理能力和問題解決能力[3].通過對翻折模型的研究和實踐,學生在解決翻折模型問題時,需要靈活運用全等性質,構造等量關系,建立方程,進行推理和論證,從而培養了他們綜合運用數學知識的能力.在教學實踐中,筆者還發現了一些問題和挑戰,比如學生對于全等性質的理解和應用存在困難,需要通過實例分析和模型演示來幫助學生理解.同時,教師在引導學生解題過程中需要不斷激發學生的求知欲和探索精神,鼓勵他們嘗試不同的解題方法,培養他們的數學思維能力.翻折模型的教學既考驗著學生的數學能力,也考驗著教師的教學水平和教學方法.通過不斷地探索和實踐,學生可以更好地引導學生掌握翻折模型的解題技巧,提升他們的數學素養,培養他們綜合運用數學知識解決實際問題的能力.
參考文獻:
[1]單小燕.初中數學解題教學策略探析——以“勾股定理中的翻折問題解題教學”為例[J].數學之友,2023,37(04): 47-48+52.
[2]沈穎.初中數學勾股定理中的翻折問題[J].現代中學生(初中版),2022,(22):3-4.
[3]劉鈺.初中數學解題課教學策略課例分析——以“勾股定理中的翻折問題”解題教學為例[J].中學數學,2021,(10):8-9+13.

