基于GARCH-GA-BP模型的股市波動率預(yù)測研究

【摘 要】波動率是衡量金融資產(chǎn)收益不確定性的重要指標，由于真實的波動率無法直接觀測，因此構(gòu)建合理的波動率模型來估計真實波動率顯得尤為重要。論文對滬深300指數(shù)收益率的波動率進行GARCH建模，并在此基礎(chǔ)上構(gòu)建了基于GARCH-GA-BP的波動率混合預(yù)測模型。實證結(jié)果表明，相對于GARCH-BP模型和GARCH-SVR模型，論文提出的基于遺傳算法優(yōu)化的GARCH-GA-BP模型能顯著提高股市波動率的預(yù)測精度。

【關(guān)鍵詞】GARCH模型；GA算法；BP模型；波動率

【中圖分類號】F832.5 【文獻標志碼】A   【文章編號】1673-1069（2024）07-0124-03

1 引言

GARCH模型因其闡明了標的資產(chǎn)收益率波動的主要特征，在金融市場風險評估領(lǐng)域的應(yīng)用最為廣泛。但是GARCH模型對數(shù)據(jù)的平穩(wěn)性和正態(tài)性有一定的前提要求并且容易出現(xiàn)過擬合的情況。近年來，隨著科學(xué)技術(shù)的加速發(fā)展，已有部分學(xué)者將機器學(xué)習(xí)方法應(yīng)用于波動率的預(yù)測中。邱冬陽等[1]對上海黃金期貨高頻數(shù)據(jù)進行預(yù)測，發(fā)現(xiàn)改進的EN-LSTM模型可以提升短期波動率的預(yù)測精度。Christensen et al.[2]運用機器學(xué)習(xí)方法預(yù)測道瓊斯工業(yè)平均指數(shù)成分股的波動率，研究發(fā)現(xiàn)3種機器學(xué)習(xí)算法（正則化、回歸樹和神經(jīng)網(wǎng)絡(luò)）均優(yōu)于HAR模型。Kyoung-Sook和Hongjoong[3]基于LSTM深度學(xué)習(xí)方法提出了一種預(yù)測股市波動率的算法，并采用2010-2016年的標準普爾500指數(shù)等5個股票市場指數(shù)的數(shù)據(jù)對算法進行了檢驗。Zhang et al.[4]應(yīng)用機器學(xué)習(xí)模型預(yù)測股票市場每日實際波動率，結(jié)果表明神經(jīng)網(wǎng)絡(luò)模型在性能方面最優(yōu)。Liu和Fu[5]利用灰色模型和極限學(xué)習(xí)機（ELM）的混合算法來預(yù)測IBOR的波動率，結(jié)果發(fā)現(xiàn)與BP和經(jīng)典ELM的預(yù)測結(jié)果相比，新模型對IBOR中短期波動率的預(yù)測效率更高。但是將機器學(xué)習(xí)算法和GARCH模型相結(jié)合的研究較少，尤其是在股票市場的波動率預(yù)測方面。如劉晨旸[6]通過構(gòu)建SVR-GARCH模型對貨幣價格波動率進行預(yù)測，發(fā)現(xiàn)其提高了原有GARCH模型的預(yù)測精度。Koo和Kim[7]采用VU-GARCH-LSTM的組合模型對標準普爾500指數(shù)的實際波動率進行預(yù)測，結(jié)果表明該混合模型的預(yù)測效果優(yōu)于LSTM-GARCH。因此本文將GARCH模型捕獲的股票市場波動性等特征信息融入BP模型的底層，并利用遺傳算法對BP神經(jīng)網(wǎng)絡(luò)進行優(yōu)化，提出了一種基于遺傳算法優(yōu)化的BP模型與GARCH模型相結(jié)合的混合模型來預(yù)測股票市場的波動率，以期提高股市收益率波動的預(yù)測精度。

2 理論基礎(chǔ)

2.1 GARCH模型

2.2 BP神經(jīng)網(wǎng)絡(luò)模型

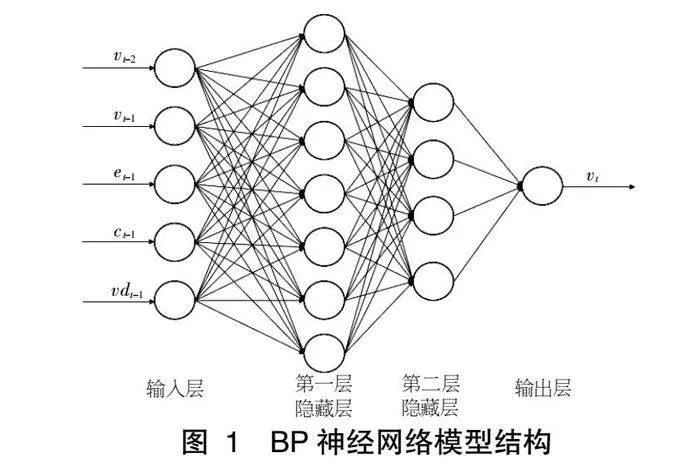
BP神經(jīng)網(wǎng)絡(luò)模型[9]是一種誤差反向傳播的多層前饋神經(jīng)網(wǎng)絡(luò)，是目前神經(jīng)網(wǎng)絡(luò)模型中最具代表性且應(yīng)用最普遍的模型，主要包括輸入層、隱藏層、輸出層。本文將預(yù)測前兩天的波動率vt-2，vt-1，前一天的極差et-1、收盤價ct-1、成交量volt-1共5個指標作為神經(jīng)網(wǎng)絡(luò)的輸入，當天的波動率vt為輸出，其結(jié)構(gòu)如圖1所示。

2.3 GA-BP模型

遺傳算法是一種基于自然選擇和基因遺傳學(xué)原理的隨機并行搜索算法。由于BP神經(jīng)網(wǎng)絡(luò)存在隨機選取初始權(quán)值和閾值的缺點，而GA算法能夠優(yōu)化其初始權(quán)值、閾值，使BP神經(jīng)網(wǎng)絡(luò)未成熟收斂得以改善，非線性映射能力得到充分發(fā)揮，且保留遺傳算法收斂速度快、學(xué)習(xí)能力強的優(yōu)良性能。GA-BP模型[10]的主要過程如下：

第一，根據(jù)訓(xùn)練集和測試集確定神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)。

第二，編碼。

第三，確定適應(yīng)度函數(shù)。

式中，SE為期望輸出值與實際輸出值之間的誤差平方之和。

第四，初始化種群并依照步驟三中的公式計算適應(yīng)度函數(shù)。

第五，根據(jù)適應(yīng)度進行選擇、交叉、變異。

第六，循環(huán)步驟三至五，直至達到訓(xùn)練目標或最大迭代次數(shù)為止。

第七，訓(xùn)練神經(jīng)網(wǎng)絡(luò)，得到最優(yōu)解。

2.4 GARCH-GA-BP模型

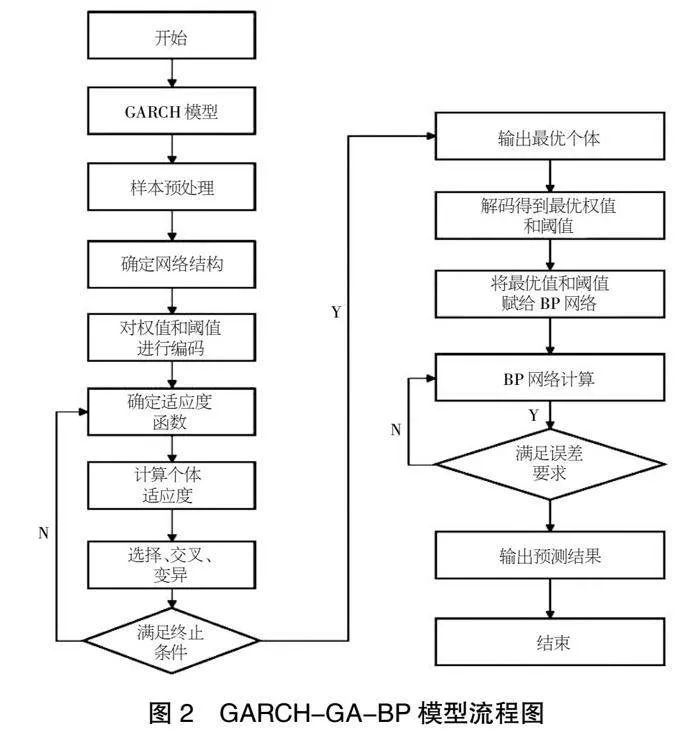
本文結(jié)合GARCH模型和GA-BP模型的優(yōu)點，構(gòu)建了GARCH-GA-BP模型，即將GARCH模型的預(yù)測值作為BP神經(jīng)網(wǎng)絡(luò)的輸入值，并通過GA算法對BP神經(jīng)網(wǎng)絡(luò)進行參數(shù)調(diào)優(yōu)獲得最優(yōu)解。算法的流程如圖2所示。

3 實證分析

3.1 數(shù)據(jù)描述性統(tǒng)計

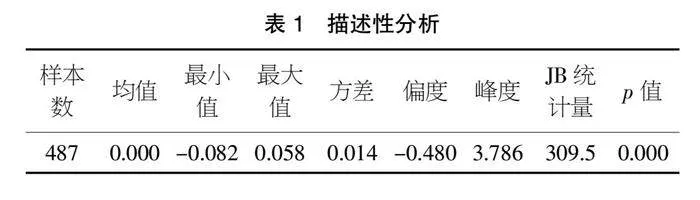
本文以2018/6/13～2020/6/13滬深300指數(shù)收益率為研究對象，表1為其對數(shù)收益率的描述性分析。結(jié)果顯示，對數(shù)收益率的均值為0，峰度為3.786，且p值為0，因此拒絕該數(shù)據(jù)服從正態(tài)分布的假設(shè)。

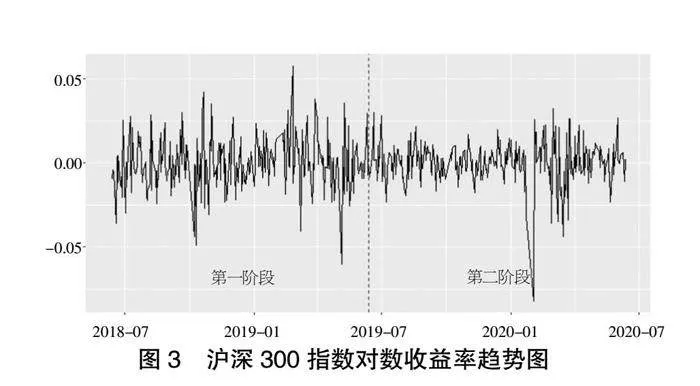
圖3為滬深300指數(shù)對數(shù)收益率趨勢圖，從圖3可以看出對數(shù)收益率存在明顯的波動聚集性，說明該序列存在異方差性。

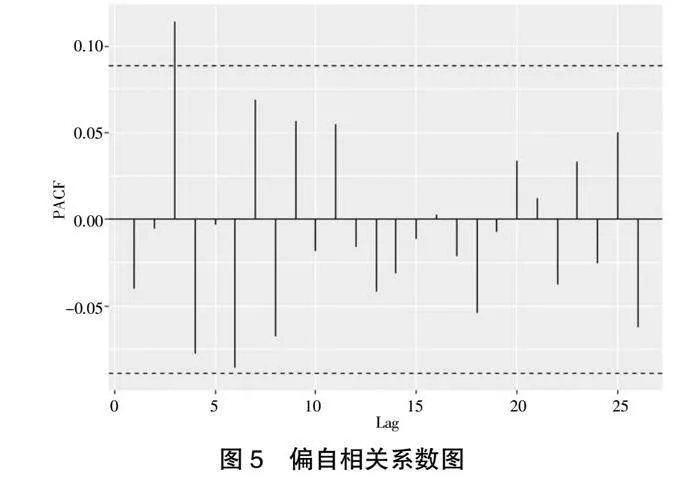
3.2 數(shù)據(jù)統(tǒng)計分析

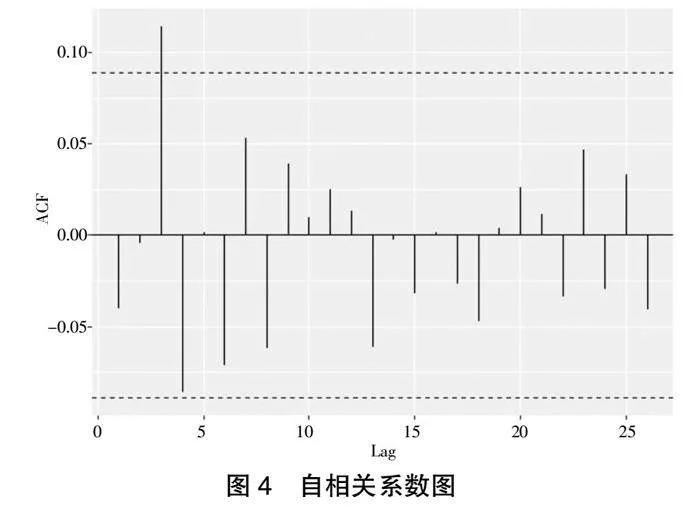
圖4與圖5分別是該指數(shù)對數(shù)收益率的自相關(guān)與偏自相關(guān)圖，可以看出該序列與滯后三階數(shù)據(jù)間存在較小的序列相關(guān)性。同時，本文利用最小AIC準則判斷，當建立ARIMA（0，0，0）時，模型的AIC最小，為-2 769.83。結(jié)合表1中滬深300指數(shù)對數(shù)收益率均值為0，本文直接建立GARCH模型，不再需要對原始序列建立均值方程。

表2為ADF平穩(wěn)性檢驗結(jié)果，從表2結(jié)果可以看出該指數(shù)對數(shù)收益率是平穩(wěn)序列，因此可以建立GARCH模型。

LM檢驗判斷序列是否存在ARCH效應(yīng)，結(jié)果如表3所示。從表3中看出p值為0.121 4，在顯著性水平為0.1的水平下不能拒絕原假設(shè)，即原對數(shù)收益率序列存在ARCH效應(yīng)。

3.3 GARCH（1，1）模型結(jié)果

考慮滬深300指數(shù)對數(shù)收益率并不服從正態(tài)分布，本文利用極大似然法估計對數(shù)收益率序列服從自由度約為4的t分布。因此，在建立GARCH模型時，本文假設(shè)序列收益率服從自由度為4的t分布。GARCH模型的系數(shù)如表4所示。

為檢驗GARCH（1，1）模型的有效性，本文對該模型的殘差進行了Ljung-Box白噪聲檢驗與ARCH效應(yīng)檢驗。Ljung-Box白噪聲檢驗的p值為0.901 6，說明殘差符合白噪聲；ARCH效應(yīng)檢驗中的p值為0.01，說明殘差不存在ARCH效應(yīng)。因此，本文建立的GARCH（1，1）模型是合理的。

3.4 波動率預(yù)測與評估

本文將樣本集劃分為訓(xùn)練集與測試集，采用滾動時間窗口的方法進行預(yù)測。其中訓(xùn)練集為2018/6/13～2020/1/15的388個樣本，測試集為2020/1/16～2020/6/13的97個樣本。選取收盤價及其極差、成交量、滯后一階及二階波動率共5個指標作為模型輸入，當期波動率作為輸出建立模型。通過計算各模型RMSE、MAE及MAPE來比較各模型的預(yù)測性能。各指標計算公式如下：

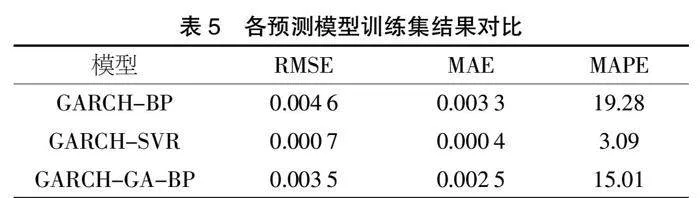
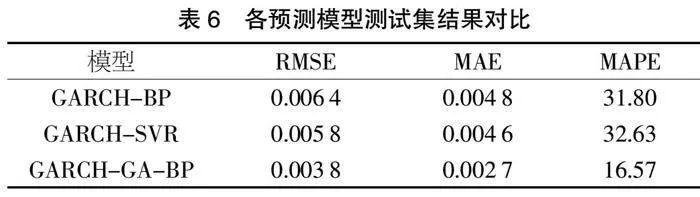
型。為了使本文提出的模型更具有說服力，本文同時加入了支持向量回歸（SVR）模型進行結(jié)果對比。模型在訓(xùn)練集與測試集的表現(xiàn)結(jié)果分別如表5與表6所示。

從表5與表6的結(jié)果可以看出，GARCH-SVR模型在訓(xùn)練集的各指標是所有模型中最小的一個，而測試集的指標要明顯高于訓(xùn)練集，可見GARCH-SVR模型容易造成過擬合現(xiàn)象。而本文提出的GARCH-GA-BP在訓(xùn)練集與測試集均表現(xiàn)出了更好的結(jié)果，說明了將GA方法應(yīng)用到神經(jīng)網(wǎng)絡(luò)參數(shù)的優(yōu)化過程中，可以很好地解決傳統(tǒng)神經(jīng)網(wǎng)絡(luò)容易達到局部最優(yōu)解的問題，并提高了模型的預(yù)測精度。

4 結(jié)論

波動率在風險管理、衍生品定價和對沖、投資組合選擇等金融領(lǐng)域都扮演著重要的角色。隨著全球金融市場一體化，對波動率模型的精度要求也在不斷提高，因此構(gòu)建合理的模型來捕捉金融資產(chǎn)收益率的波動，度量金融市場的風險，對投資者和監(jiān)管部門都具有重要的理論和實踐意義。本文以滬深300指數(shù)收益率作為研究對象，提出了基于遺傳算法優(yōu)化的GARCH-GA-BP波動率預(yù)測模型，結(jié)果發(fā)現(xiàn)：基于遺傳算法優(yōu)化的GARCH-GA-BP模型的預(yù)測精度明顯優(yōu)于GARCH-BP模型和GARCH-SVR模型，且與GARCH-BP模型相比，測試集上的RMSEBsJwZL0wURKscI8YZ3Ukhg==、MAE及MAPE值分別降低了40.63%、43.75%和47.89%。

【參考文獻】

【1】邱冬陽，丁玲，何一夫.基于高頻數(shù)據(jù)和EN-LSTM的黃金期貨短期波動率預(yù)測[J].運籌與管理，2024，33（03）：184-190.

【2】Christensen K， Mathias S， Bezirgen V. A machine learning approach to volatility forecasting[J].Journal of Financial Econometrics，2023，21（5）：1680-1727.

【3】Kyoung-Sook M， Hongjoong K I M. Performance of deep learning in prediction of stock market volatility[J]. Economic Computation & Economic Cybernetics Studies & Research，2019，53（2）：77-92.

【4】Zhang C， Zhang Y， Cucuringu M， et al. Volatility forecasting with machine learning and intraday commonality[J]. Journal of Financial Econometrics，2024，22（2）：492-530.

【5】Liu X， Fu H. Volatility forecasting for interbank offered rate using grey extreme learning machine： The case of China[J]. Chaos， Solitons & Fractals， 2016（89）：249-254.

【6】劉晨旸.基于SVR-GARCH的貨幣波動率預(yù)測研究——以加密貨幣和傳統(tǒng)貨幣為例[J].國際經(jīng)貿(mào)探索，2023，39（01）：52-67.

【7】Koo E， Kim， G. A hybrid prediction model integrating garch models with a distribution manipulation strategy based on lstm networks for stock market volatility[J].IEEE Access，2022（10）：34743-34754.

【8】Bollerslev Tim. Generalized autoregressive conditional heteros-kedasticity[J]. North-Holland，1986，31（3）：307-327.

【9】崔文喆，李寶毅，于德勝.基于GARCH模型和BP神經(jīng)網(wǎng)絡(luò)模型的股票價格預(yù)測實證分析[J].天津師范大學(xué)學(xué)報（自然科版），2019，39（05）：30-34.

【10】薛倩男，高岳林.基于時間序列的GA-BP神經(jīng)網(wǎng)絡(luò)股價預(yù)測模型[J].蘭州文理學(xué)院學(xué)報（自然科學(xué)版），2017，31（05）：46-49.