找準目標巧妙切入，分類討論引領思想

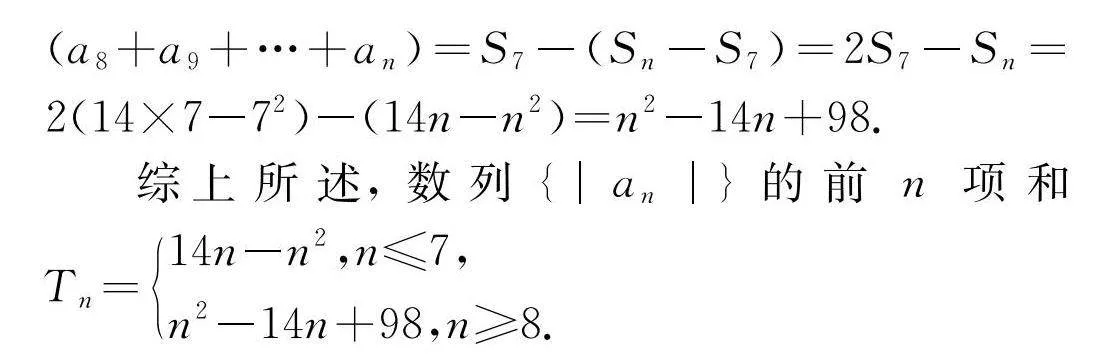
摘要：分類討論思想作為基本數學思想之一，其應用一直是高考數學試卷命題的一個重要方向.本文結合分類討論思想切入目標的尋找與確定，從不同層面加以展開與應用，并結合2023年高考真題進行剖析，探尋目標切入點，全面歸納總結應用技巧，指導并引領數學教學與復習備考.

關鍵詞：分類討論思想；集合；函數；數列分類討論思想是高考數學中經常用到的基本數學思想，其滲透于高考真題的方方面面.該思想可以將一個復雜的數學問題巧妙分解或分割成一些比較簡單的基本性問題.

本文結合2023年高考真題中的實例，就分類討論思想，從不同層面的切入，基于概念應用、參數取值、圖形位置以及運算結果等不同場景，剖析分類討論思想，切入目標方法，實現問題的突破，巧妙綜合應用.

1抓住概念、法則、公式等進行分類討論

數學中一些核心數學概念、法則以及公式是基于分類討論思想構建的，如數學概念中絕對值的定義、分段函數的定義，數學公式中等比數列的求和公式等.在解決一些涉及函數、不等式、數列知識的問題時，經常要借助分類討論思想來切入.

例1（2023年全國新高考Ⅱ卷第2題）設集合A={0，－a}，B={1，a－2，2a－2}，若AB，則a=（）.

A. 2B. 1C. 23D. －1

分析：解題時抓住兩個含參數集合間的包含關系，結合集合中元素的互異性，合理構建對應的方程，就不同方程所求得的參數值進行分類討論，結合參數值的取值情況以及對應的集合，進行必要的判斷與取舍.

解析：由題可知，AB，則a－2=0或2a－2=0.當a－2=0時，解得a=2，則A={0，－2}，B={1，0，2}，不滿足條件AB，舍去；當2a－2=0時，解得a=1，則A={0，－1}，B={1，－1，0}，滿足條件AB.綜上分析，a=1，故選擇答案B.

點評：熟練理解并掌握數學基礎知識中的相關概念、法則、公式等，是數學學習的基礎，也是問題目標切入的方向

，更是解決相關問題對分類討論思想應用的依據與根本.在該問題中，兩個集合間的包含關系及其概念為利用分類討論思想解決問題提供了條件.

2結合參數取值、變量變化等進行分類討論

一些涉及參數取值、變量變化的實際問題，如含參的函數、方程或不等式等應用問題，往往也離不開分類討論思想的應用，解題時要依托參數的分類來深入分析與求解.分類討論思想給問題的解決提供了基本的解題思維.在分類討論中，一定要注意對參數取值、變量變化的全部情況進行討論，不能出現遺漏與偏差.

例2（2023年全國新高考Ⅰ卷第19題）已知函數f（x）=a（ex+a）－x，討論f（x）的單調性.

分析：解題時依托含參函數及其表達式，結合參數a的取值情況加以分類討論，在a≤0與a>0兩種不同情況下，結合導函數進行分析與處理，探究函數的單調性.

解析：由題可知，f（x）的定義域為R，且f′（x）=aex－1.

當a≤0時，f′（x）<0，故函數f（x）在R上單調遞減.

當a>0時，令f′（x）=aex－1=0，解得x=－lna，則當x∈（－∞，－lna）時，f′（x）<0，故函數f（x）在（-∞，-ln a）上單調遞減；當x∈（－lna，+∞）時，f′（x）>0，故函數f（x）在（-ln a，+∞）上單調遞增.

綜上分析，當a≤0時，函數f（x）在R上單調遞減；當a>0時，函數f（x）在（－∞，－lna）上單調遞減，在（－lna，+∞）上單調遞增.

點評：在解決一些含參數或變量的數學問題時，往往要結合參數、變量的取值或變化以及對所求結果的影響等方面進行合理的分類討論，在不同場景下探討不同的結果.需要注意的是，在確定參數或變量的取值時，分類討論要做到分類標準明確，不重不漏.

3利用圖形位置、幾何形狀等進行分類討論

數學中一些圖形（平面圖形、曲線、立體圖形等）的應用問題，往往依托直觀想象，給分類討論提供了更多的應用場景，如圖形中相關點的變化情況的分類討論，函數圖象的變形情況的分類討論，立體幾何圖形中相關元素的位置變動情況的分類討論等，都可以采用分類討論思想來探究.

例3（2023年全國甲卷文科第16題）在正方體ABCD-A1B1C1D1中，AB=4，O為AC1的中點.若該正方體的棱與球O的球面有公共點，則球O的半徑的取值范圍是.

分析：解題時利用正方體與球O的位置關系及其變化規律，確定當球O是正方體的外接球時半徑達到最大，當正方形是球O的大圓的內接正方形時半徑達到最小.利用圖形的不同情況加以分類討論，確定球O的半徑的最大值與最小值.

解析：設球O的半徑為R，當球O是該正方體的外接球時，恰好經過正方體的每個頂點，此時所求的球O的半徑最大.若球O的半徑變得更大，球會包含正方體，導致球面和棱沒有交點.正方體的外接球直徑2R′為該正方體的體對角線長AC1=43，即2R′=43，解得R′=23，故Rmax=23.

如圖1所示，分別取正方體的側棱AA1，BB1，CC1，DD1的中點M，H，G，N，顯然四邊形MNGH是邊長為4的正方形，且O為正方形MNGH對角線的交點.連接MG，可得MG=42，當球O的一個大圓恰好是四邊形MNGH的外接圓時，球O的半徑達到最小，即Rmin=22.

綜上分析，R∈［22，23］，故答案為［22，23］.

點評：對于一些與圖形有關的數學問題，如函數問題、幾何問題等，可借助平面幾何或立體幾何圖形的構建，隨著點、線、面等的變化，按照圖形位置的不同、形狀的差異變化等來進行必要的分類討論.

4應用運算結果、性質展開等進行分類討論

數學中一些結果問題，也可以借助分類討論思想來分析或求解，如指數函數與對數函數中含參的分析與求解便離不開對底數的分類討論，探究函數的單調性時也離不開對導函數正負取值的分類討論等，都是依托代數式、關系式等運算變形后的結果來深入分析與應用.

例4（2023年全國乙卷文科第18題）記Sn為等差數列{an}的前n項和，已知a2=11，S10=40.

（1）求{an}的通項公式.

（2）求數列{|an|}的前n項和Tn.

分析：第一小問借助基本量法確定數列{an}的通項公式后，第二小問中，利用含絕對值的數列關系式來構建新數列，通過對項數的不同取值加以分類討論，進行數列求和與應用.

解析：（1）設等差數列{an}的公差為d.

由題可知，a2=a1+d=11，

S10=10a1+10×92d=40，解得a1=13，d=-2，所以an=13－2（n－1）=15－2n.

（2）由（1）可知，a1=13，an=15－2n，則Sn=n（13+15-2n）2=14n－n2.

令an=15－2n>0，則n<152，且n∈N*.當n≤7時，an>0，Tn=|a1|+|a2|+…+|an|=a1+a2+…+an=Sn=14n－n2；當n≥8時，an<0，Tn=|a1|+|a2|+…+|an|=（a1+a2+…+a7）－（a8+a9+…+an）=S7－（Sn－S7）=2S7－Sn=2（14×7－72）－（14n－n2）=n2－14n+98.

綜上所述，數列{|an|}的前n項和Tn=14n-n2，n≤7，n2-14n+98，n≥8.

點評：解決涉及數學運算、基本性質等的應用問題時，需要根據絕對值的性質、函數的基本性質、指數或對數的運算與性質等進行必要的分類討論，為問題的進一步解決指明方向.本題借助分類討論思想來確定不同條件下數列求和公式的表達式，利用“分段函數”形式來表示，是本題的一大亮點.

作為基本數學思想之一的分類討論思想，是解決問題的一種重要邏輯方法，一直是歷年高考中的一個重點與熱點內容，成為高考命題的一個重要靈魂思想，在解決問題中被廣泛應用.在實際解題與應用過程中，要回歸數學內涵與本質，從教材入手，由知識引領，抓問題應用，提煉數學思想方法，并通過合理的分類、歸納與遷移，熟練掌握.巧妙應用分類討論思想，能夠有效提升學生數學思維，提高學生數學關鍵能力，培養學生數學核心素養.