聚焦幾何直觀?共創多元課堂

在當前的教育領域，構筑多元化的學習課堂，培養學生的素養，已經成為教學的新趨勢。在這一背景下，小學數學作為兼具基礎性和抽象性的學科，為了加深學生的理解，使每個學生都有所收獲，教師應重視教學方式方法的創新，而聚焦幾何直觀實施教學，以直觀的方式引領學生理解概念、性質等，能夠幫助學生構建對數學知識的感性認知，促進學生深度學習的發展。因此，小學數學教師應積極探尋聚焦幾何直觀下，多元課堂的構建路徑，以提升學生的學習品質，為學生之后的學習奠定基礎。

一、幾何直觀的相關概述

幾何直觀是小學數學素養中的重要維度，也是培養學生空間想象力及思維意識的關鍵要素，其主要是指學習者對知識屬性的直接感知和理解能力。在小學數學中聚焦這一能力開展多元化的教學工作，不僅能夠幫助學生對抽象的數學知識進行深度認知，還能調動其學習熱情，使學生更深入地汲取數學知識，領悟其中的奧秘。

二、小學數學中聚焦幾何直觀構建多元課堂的重要性

（一）培養學生的空間想象力

聚焦幾何直觀開展數學教學，可以通過圖形或者模型等，對抽象的數學知識進行形象化的解釋。在這一過程中，教師引領學生對圖形進行有效觀察，可以使學生更直觀地感受形狀、大小以及位置等空間概念，進而逐漸形成對空間結構的感知能力，這對學生空間想象力的提升有重要幫助。

（二）發展學生的邏輯思維能力

幾何直觀不只是視覺上的一種感知，更是對邏輯進行推理的過程。在實踐教學工作中，教師引領學生以觀察、推理等方式進行學習，能夠使學生發現數學知識間的關系與規律，有利于學生構建嚴密的思考框架。同時，聚焦幾何直觀的應用，讓學生自主參與數學知識的推導，能夠切實促進學生思考，提升學生的思維水平。

（三）促進學生深度學習

對一些學生而言，其在學習數學知識時常常感到困難重重，對知識的理解浮于表面。而聚焦幾何直觀構建多元化的課堂，教師不僅會從知識表面向學生闡述推導過程，還會引導其依托圖形或者視頻的輔助，從更深層次的角度探尋所學知識間的關聯，從而使學生逐漸建立起知識間的聯系，形成完整的知識網絡，這是促進學生應用意識深入發展的有效途徑。

三、小學數學中聚焦幾何直觀構建多元課堂的策略

（一）巧用幾何直觀，驗證數學猜想

在小學數學教學中，為了啟發學生的思維，增強學生的學習動機，教師通常會讓學生經歷各種形式的數學猜想，通過猜想激活學生的好奇心，調動其探究知識的欲望，但是如何驗證這些猜想也是一個挑戰。教師可以聚焦幾何直觀，發揮其作用，幫助學生以直觀的方式對猜想的內容進行驗證，以此讓抽象的數學問題變得具體而生動，也能讓學生在驗證猜想的過程中形成分析問題、思考問題與解決問題的能力，培養學生的核心素養。

例如，教師在帶領學生探究“三角形內角和”的特征時，通過測量三角形的內角，學生發現它們的和都接近 180°，于是大膽猜想：會不會所有三角形的內角和都是 180°呢？當部分學生發現三角形三個內角和可以采用拼或折的方法驗證時，教師借助幾何直觀，讓學生動手將手里的三種三角形撕一撕、折一折，并在同屏器下展示將三角形的三個內角拼成一個平角的過程。這種直觀的演示驗證了學生的猜想：所有三角形的內角和都是180°。

再如，在教學北師大版二年級上冊第六單元中的“米和厘米”內容時，為了讓學生認識米、厘米的長度單位，建立長度觀念，能夠運用計量工具測量物體長度，培養其估測及操作能力，教師可以巧用幾何直觀的方式讓學生驗證數學猜想，進而將所學知識逐步內化。首先，教師引導學生觀察不同長度的物體，如鉛筆、書本、教室的寬度等，并提問：“如何準確地描述這些物體的長度？”從而激活學生的表達興致，為探究活動的開展做好鋪墊。其次，為了讓學生更好地理解長度單位，教師可以引導其運用不同的物品（如積木、尺子等）構建幾何模型，如學生可以用積木排列出一個1米長和十個10厘米長的直線模型，以此直觀感受“米”和“厘米”的實際長度，并通過比較和測量加深對長度關系的理解。最后，在學生有了直觀感受后，教師提出一個數學猜想：“若一個物體的長度是1米，那么它的長度也可以是多少厘米呢？”學生通過之前構建的幾何模型（1米和10個十厘米）來進行驗證，從而持續融入本課重點知識，有效培養學生的觀察與思考能力。

（二）巧用幾何直觀，揭示概念本質

數學概念是抽象文字的堆砌，將這些文字組合在一起，引領學生汲取數學知識，學生常常倍感困惑，很難理解概念的本質。因此，在現階段的小學數學教學中，為了強化學生對概念知識的掌握，教師可以巧用幾何直觀解讀數學概念的本質，將抽象的數學概念與形象具體的幾何圖形分析進行融合，使學生通過對數學圖形的解讀深化理解認知，以此促進學生對數學概念的深度探究。

例如，在教學北師大版三年級下冊第六單元“認識分數”這一內容時，這部分的概念知識對學生來說有一定的理解難度，教師可以基于學生的生活經驗創設分蘋果的情境：把1個蘋果平分給2個人，每人分到這個蘋果的一半（半個蘋果）。首先，教師引導學生嘗試用畫圖的方法表示“一半”，認識表示“一半”的分數；其次，讓學生在方格紙上涂出圖形的一半，就是涂出圖形面積的二分之一，進一步理解二分之一的分數意義；最后，用折紙涂色的方法（或畫圖的方法）“創造”更多的分數，體會分數是表示一張紙的涂色部分與這張紙之間關系的一個數。以上畫一畫、涂一涂、折一折等直觀操作的目的都是引導學生經歷分數的產生和發展過程，從而理解分數的概念本質。這種利用幾何直觀，以演示法達到教學目標的方式，能夠帶給學生視聽結合的學習盛宴。在這一過程中，教師的舉動牽動著學生的思維，學生的學習熱情高漲，對概念知識的理解也非常迅速，并有效促進了多元課堂的構建。

（三）巧用幾何直觀，理解計算道理

計算教學要重視在研究“怎么算”中明白算理，教師可以大膽地釋放空間，讓學生借助圖形各抒己見，充分說理交流，培養數感，將算式變成圖形，化抽象為形象。

例如，在北師大版一年級下冊“采松果——兩位數加（減）一位數”教學中，對于不進位加法的口算，重點要理解為什么要使相同數位的數相加。教師應組織擺小棒、撥計數器以及在數線上畫一畫的數學活動，讓學生通過直觀的動手操作，明白所加的數是幾個一還是幾個十。如果是幾個一就加在個位上，是幾個十就加在十位上，給予學生充足的思考、交流和表達的時間，使學生在觀察與交流中掌握兩位數加減一位數的算理和算法，在操作中學習，在學習中領悟，真正成為學習的主人。

再如，“螞蟻做操”是北師大版三年級上冊的內容，讓學生借助點子圖這一直觀模型，理解乘法豎式每一步的含義。首先，教師讓學生在點子圖上圈一圈，算一算。其次，讓學生與同伴說說計算過程，以及自己是怎么圈的。最后，結合圈的結果說一說先算什么，再算什么。這部分教學注重學生在實際觀察、操作等活動中獲得直接經驗，通過一連串的活動感悟計算過程的含義，理解兩位數乘一位數的算理，從而讓學生經歷知識形成的全過程。

（四）巧用幾何直觀，促進問題解決

在小學數學教學中，幾何直觀是連接抽象概念與具體理解的橋梁，不僅可以幫助學生驗證數學猜想，揭示數學概念本質，還能幫助學生以形象的方式理解計算的道理，激發學生的學習興趣，促進學生思維意識的形成。因此，在聚焦幾何直觀構建多元化的數學學習課堂時，教師可以巧用繪制圖形的方式，讓學生觀察看到的圖形，并結合學生的生活實際，提出思考性的問題，鼓勵學生發散思維，形成幾何直觀素養，從而有效解決問題，提升學習效率。

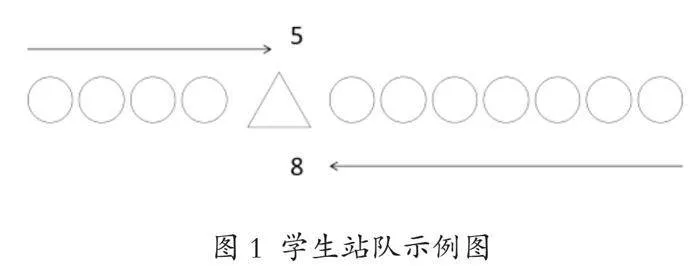
例如，在教學北師大版一年級上冊第一單元“生活中的數”課程內容時，本課旨在讓學生掌握二十以內的數，培養學生的數感。在實踐教學中，為了扎實學生的知識基礎，為之后的學習做好鋪墊，使其具備解決問題的能力，教師可以將知識與學生的實際生活相關聯，巧用幾何直觀的方式實施教學，如以體育課上學生站隊為例：“從前往后數，第5個是學生A；從后往前數，第8個也是學生A，請問該隊伍共有幾名學生？”面對教師提出的這一問題，一些學生表現得不知所措，無法理解題干的真正含義。這時，教師可以巧用幾何直觀實施教學，以抽象的幾何符號“△”“□”“○”等替代題目中的學生，用“△”表示學生A，用“○”表示其他學生（如圖1所示），進而列出算式“5+8-1”，得到問題的正確答案。這種借助抽象符號的方式將知識轉化為幾何圖形，既能使學生快速地解決問題，也能有效培養學生的幾何直觀素養。由于積累了相關的學習經驗，未來在面對類似的問題時，學生也能從容冷靜地應對，快速找到解決方法，以此發展學科素養。

（五）巧用幾何直觀，培養表達慣性

第一，養成畫圖的習慣。在聚焦幾何直觀開展小學數學教學工作時，教師既要巧用幾何直觀讓學生去理解所學知識，還應著重培養學生的畫圖能力，使其生成這樣的習慣技能，從而在面對具體的數學問題時，能夠借助幾何直觀的方式更快、更準確地予以解決。而這一能力的培養需要學生自身養成思考的習慣，更需要教師的示范、指導與點撥，以有效豐富解決數學問題的輔助手段，助力學生可持續發展。首先，這種習慣源自學生的自我需求。小學數學知識的編排難度呈遞進關系，越往后難度越大，尤其是平面圖形的周長、面積以及立體圖形的表面積等知識，都需要直觀圖的支撐。在學生學習這些知識遇到困難時，教師就可以引導其利用畫圖的方式解決，讓畫圖成為學生解決問題的自我需求。以“某分數分子與分母相差15，約分后的結果為4/7，求原分數”這一習題為例，未畫圖時，很多學生會運用分數的基本性質，以列舉的方法計算，而在畫圖后，學生能夠更直觀、更快速地得到準確答案，解決學習中的困頓。其次，這種習慣還源自教師的要求。從教學實踐來看，大多數學生不理解畫圖的意義，缺乏通過畫圖解決問題的意識，教師應及時給予其指導，讓學生明確畫圖學習的重要性，從而在潛移默化中形成這樣的學習意識，能夠常常思考“能否運用畫圖對題意進行直觀表達，以及如何表達更為準確”，以此提升學生的思考水平，促進學生學科素養的發展。

第二，用圖像語言表達。在學生形成用幾何直觀解決數學問題的意識和習慣后，教師應將其落實到實踐中，著重引導學生經歷持續的問題分析階段，并結合圖形描述的方法，幫助學生構建通過圖像直觀解決問題的傾向，使學生熟練借助圖像工具進行文字表達，真正實現聚焦幾何直觀構建多元課堂的目標。這一過程能夠有效發展學生的幾何直觀意識，使學生借助畫圖的手段展示數學思考過程，加深對數學知識本質的了解。因此，教師應為學生提供更多元的發展空間，在出示問題后，引導學生遵從自己的本心進行解決，而后給予其指導，使學生在對比、思考、分析中逐漸明確用圖像表達語言的重要意義。

例如，在教學北師大版五年級上冊第四單元“多邊形的面積”課程內容時，進入五年級，數學知識的學習難度大幅增加，很多學生不適應，難以建立知識間的聯系，教師可以向學生出示以下習題：若平行四邊形與三角形等底，其高是三角形的2倍，那么它的面積是三角形面積的幾倍？該問題較為抽象，教師可以先讓學生以自主思考的方式解答，這時班級學生給出了不同的解題路徑，有的學生用文字及計算對推理過程進行描述，有的學生則運用畫圖的方式解決問題，很顯然，畫圖的學生給出的答案更加明了，這極大地加強了學生的認知。這種用圖像進行語言表達的方式離不開學生畫圖習慣的養成，也與教師以往有意識地引導和訓練密切相關，使學生自然而然地形成了幾何表達的慣性。同時，教師應給予學生針對性的引導，使其明確如何更直觀、更快速地解決問題。

四、結語

總而言之，幾何直觀是小學數學教學中的重要素養，聚焦其構建多元化的數學課堂，不僅有利于培養學生運用圖像解決問題的能力，還能強化其學習效能，提高其可持續發展水平。因此，在實踐教學工作中，教師應積極探尋教學路徑，通過巧用幾何直觀驗證數學猜想、揭示概念本質、理解算理、促進問題解決以及培養圖形表達慣性的方式，構筑高效的數學課堂，使課堂綻放生機與活力。