“大概念”視角下小學數學教學實踐研究

摘要：“大概念”視角下的教學實踐源于“大概念”視角下的課前研究。課堂是實施“大概念”視角下教學的主要載體，教學評價是保障“大概念”視角下教學的重要手段。“大概念”視角下的小學數學教學是新時代的呼喚，也是數學學科的本質要求。

關鍵詞：“大概念” 小學數學 計數單位

學科“大概念”反映學科的本質，是指具有較為廣泛的適用性和解釋力的原理、思想和方法。數學學科具有結構性和嚴謹性，這就需要借助“大概念”來確定知識主線，從而將零散的數學知識整合，打破知識之間的壁壘，設計有序的知識塊，有效促進學習遷移。

2022年，教育部發布新版《義務教育數學課程標準》，其中對“數與代數”領域的內容進行結構化整合。在教學運算缺乏一致性的現實背景下，新課標將數的認識和數的運算綜合為“數與運算”。數的運算即相同計數單位的累加，其中“計數單位”就是數學體系中的一個“大概念”。在這一“大概念”的統領下，無論整數、小數還是分數都是由多個相同計數單位組成，加減乘除等運算都是計算相同計數單位。

筆者以蘇教版六年級上冊“分數與整數相乘”為例，談談如何基于“大概念”視角開展教學實踐。

一、課前研究

（一）目標要求與教材內容分析

1.新課標目標要求

“分數與整數相乘”是蘇教版六年級上冊第二單元的第一課時，屬于數與運算領域。新課標明確規定其目標是能進行簡單整數、小數及分數運算，探索運算一致性。所謂運算一致性對于小學階段的乘法運算而言，就是相同計數單位的累加。因此，運算教學中明確大概念即“相同計數單位累加”。

2.教材內容分析

從縱向角度，蘇教版教材自二年級上冊開始學習乘法意義，逐步遷移學習整數乘法、小數乘法和分數乘法。教學實踐中就一課講一課，割裂了知識的本質聯系，造成知識學習的單一性和片面性。

從橫向角度，本單元安排的層次是先學習“分數與整數相乘”——實質是求幾個幾分之一，再學習“求一個數的幾分之幾”——拓展分數乘法的意義，最后學習“分數與分數相乘”——實質是求幾個幾分之一。思維方向的不同，也會影響學生對分數乘法的學習。

（二）學情分析

為準確了解學生的學情，筆者對學校五年級47名學生，主要從算法和意義的角度來進行前測。

1.算法角度

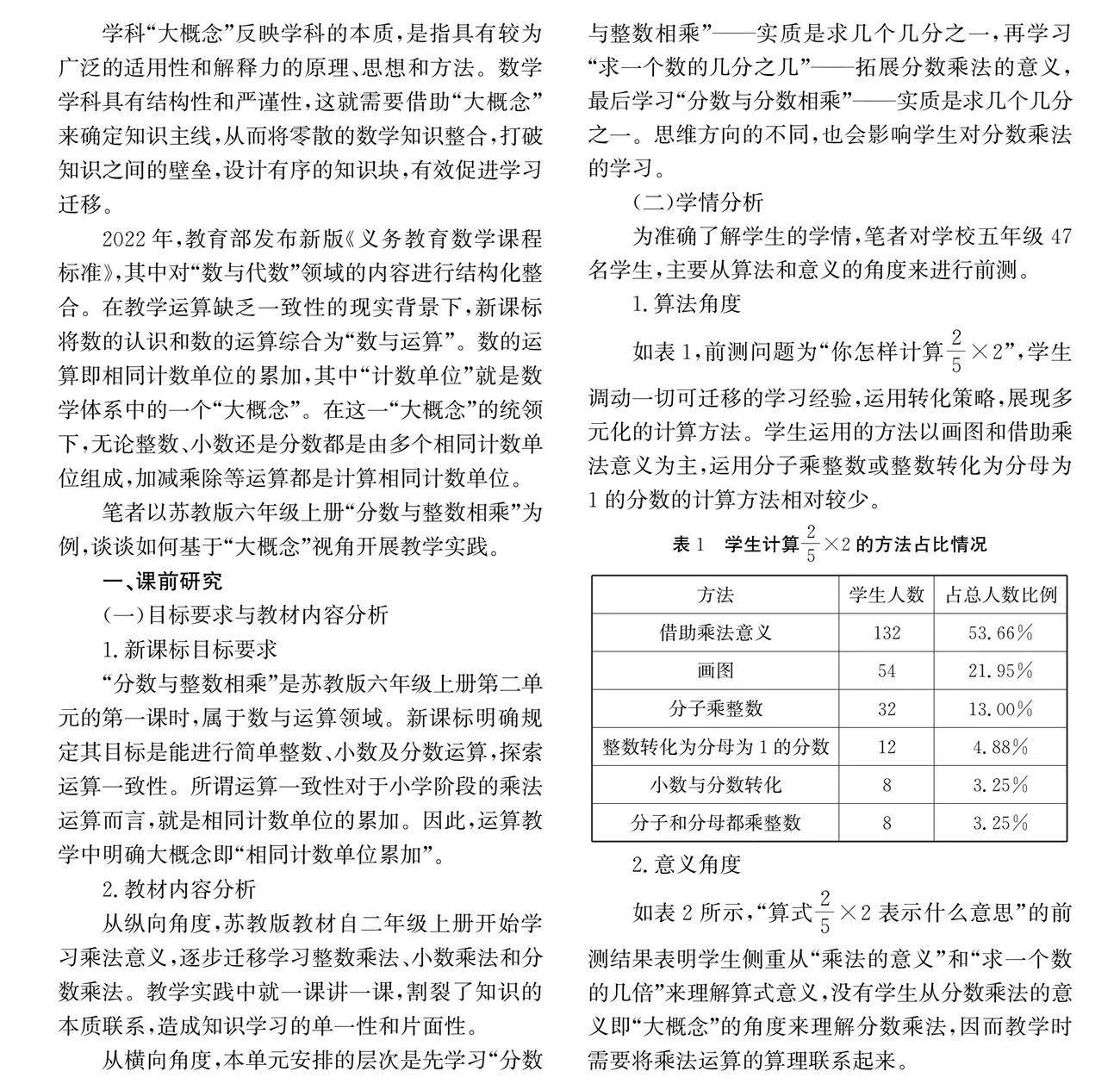
如表1，前測問題為“你怎樣計算25×2”，學生調動一切可遷移的學習經驗，運用轉化策略，展現多元化的計算方法。學生運用的方法以畫圖和借助乘法意義為主，運用分子乘整數或整數轉化為分母為1的分數的計算方法相對較少。

2.意義角度

如表2所示，“算式25×2表示什么意思”的前測結果表明學生側重從“乘法的意義”和“求一個數的幾倍”來理解算式意義，沒有學生從分數乘法的意義即“大概念”的角度來理解分數乘法，因而教學時需要將乘法運算的算理聯系起來。

二、課堂實踐

（一）問題導入 回顧舊知

本課程實踐將蘇教版教材中直接展示的情境調整為兩個問題。學生根據已有經驗解決問題，列出整數與整數相乘、小數與整數相乘的算式，順勢引出課題“分數與整數相乘”。

問題1：做一朵綢花需3分米綢帶，做3朵一共需多少分米綢帶？

問題2：做一朵綢花需0.3米綢帶，做3朵一共需多少米綢帶？

【設計意圖】一方面通過問題激發學生興趣和回顧舊知，乘法運算分為整數乘法、小數乘法以及分數乘法，學生列出整數與整數相乘和小數與整數相乘的算式，順勢引入分數與整數相乘；另一方面在導入環節生成的素材，為后續整體建構知識，感悟屬于運算的“大概念”打下基礎，有利于學生更完整地體驗乘法運算的算理。

（二）探索算法 明晰算理

1.創設情境，明確題意

首先，創設學校布置校園需要制作綢花的情境，出示條件“做一朵綢花要用310米綢帶”。為明確310米有多長，教材直接出示條件完整的示意圖。本課程實踐中，為了讓學生體驗過程和運算一致性，設計讓學生通過操作畫圖來體驗310米有多長，從分數單位的角度認識分數。

【設計意圖】鼓勵學生自主完成學習單任務一（如圖1）。長1米的空白條形圖將抽象的分數轉化為可直觀的圖，易于學生從分數單位角度理解分數。學生通過具體的操作過程深刻體會到涂了3段，量化了310米，它有3個110米，為后續計算分數乘法做鋪墊。

任務二：小芳做3朵綢花，一共要用多少米綢帶？

用你喜歡的方式表示出“310×3”的思考過程。（可以畫一畫 算一算）

2.嘗試列式，尋求算法

在明確310米有多長之后，出示“做3朵一共多少米綢帶”的問題。學生結合乘法意義，列出分數與整數相乘的算式“310×3”。在理解算式的含義后，鼓勵學生聯系舊知用自己喜歡的方式表示“310×3”的思考過程。蘇教版教材直接展示加法和乘法兩種計算方法。本課程實踐中為明確知識的內在邏輯，設計學習單任務二（如圖2），鼓勵學生充分調動一切可利用的知識經驗來解決問題。

學生運用知識經驗展示以下四種方法（如圖3），對比發現四種方法都是將“310×3”轉化為已有知識來解決，由此提煉出“轉化”策略。學習單任務能激勵學生主動學習，同時整合知識。在梳理算法的過程中，進一步梳理算理：方法一可以理解為9個1分米累加，方法二可以理解為9個0.1米累加，方法三可以理解9個110米累加。這些方法都是從計數單位的角度來理解整數乘法、小數乘法以及分數乘法的算理。

方法一 單位轉化

方法二 轉化為小數乘法

方法三 轉化為加法

方法四 轉化為畫圖策略

【設計意圖】通過前期學情調研，學生運用多元化方法來解決問題。比較多種方法，都是將未知轉化為已知來解決問題，從而提煉出“轉化”策略，培養學生解決問題的能力。每種方法都是從“大概念”的角度來解決問題，方法一本質是“9個1分米”相加，方法二本質是“9個0.1米相加”，方法三本質是“9個110米相加”，學生初步體會從計數單位的角度來運算。

3.再次嘗試，完善認知

在學生逐步明確算法后，出示學習單任務三，將教材中“5朵”綢花調整為

“15朵”，一方面鞏固算法，另一方面用更大的數據讓學生體會到約分的必要性。結合之前的算法，學生直接用分子與整數相乘，展現兩種方法：一種是先計算，再約分；另一種是先約分，再計算。對比兩種計算方法（如圖4），學生經過思考后發現，后一種方法更為簡便。在前面學習的基礎上，自主總結歸納算法：能約分的，先約分。

先計算，再約分

先約分，再計算

【設計意圖】教材中直接引導學生思考能約分的先約分。本課程實踐中突出學生自主性，讓學生比較兩種算法，經歷優化算法的過程，深刻理解“先約分再計算”更簡便，體會分數乘法中先約分的好處。

4.鞏固練習

涂一涂，要求先在長方形中涂出4個316，再算出涂色部分一共是這個長方形的幾分之幾。

【設計意圖】學生借助圖形明確分數乘法是計算相同的分數單位。先通過畫圖明確1個316有多少個116，再借助畫圖思考實質是計算有多少個116。

（三）整體架構 豐富認知

回顧三道算式（見圖5），首先理解整數乘法“3×3”。“×”之前的“3”表示有3個1，這里通過3個1，學生易于理解“3個1”是一個整體，“×”后面的“3”表示有3個“3個1”，學生在運算過程中理解“3×3”的結果為“9個1”；通過類比的方法來理解小數乘法“0.3×3”和分數乘法“310×3”。對比三道乘法算式，教師引導學生一步步發現“1”“0.1”“110”分別是“3×3”“0.3×3”“310×3”的計數單位。以上三道算式結果中都有9，提煉出9表示計數單位的數量。學生通過小組討論，明白整數、小數、分數的乘法運算都是相同計數單位的累加。

【設計意圖】在掌握算法和理解算理后，引導學生回顧之前的整數乘法、小數乘法、分數乘整數算法。在“相同計數單位”的大概念基礎上，引導學生體會運算一致性。

四、課后反思

（一）“大概念”視角下的課前研究

教師在教學設計和實踐之前，必須做好課前研究：認真研讀課程標準，從“大概念”視角出發，吃透內容的本質，明確“核心概念”；同時，研磨教材，從橫向和縱向全方位和多角度思考知識的內在聯系；精準分析學生情況，針對學習內容設計相關評測，真實了解學生的情況。教師應基于學情調查、教材分析、課標研究，科學制定教學目標，確定教學重難點。目前學生鮮少從“大概念”視角認識數的運算。我們不能只拘泥于學習分數與整數相乘的算法和算理，還要引導學生在經歷探索分數與整數相乘的算理算法的過程中，體會數學知識的內在聯系，體悟乘法運算是相同計數單位的累加，為今后學習分數與分數相乘、分數除法等知識做鋪墊。

（二）“大概念”視角下的學習活動

數學學科的結構性很強，應以學生主動學習為核心，遵循知識的內在邏輯和學生的認知規律，通過自主性的學習活動建構知識體系，促進學習遷移。于本課而言，教師可通過三個任務驅動學生自主探究，激活已有認知經驗，促進學生主動學習知識。

（三）“大概念”視角下的教學評價

現代評價發展觀強調結果，更強調過程，它是保障教學的重要手段。基于“相同計數單位累加”的大概念視角，本課既考慮到學前情況，進行學前評測，同時也十分注重學生在課中的生成性成果，鼓勵學生展示交流，激發學習動機。教師結合前期研究設計了有意義的任務，利用任務驅動學生自主學習，在學習新知后，設計兩道緊緊圍繞“大概念”的練習題，注重學生的進步。以上都需要多元、多樣以及恰當的教學評價，幫助教師全面了解學生學習的過程和結果，為下一節課的教學指明方向并提供參考。

參考文獻：

［1］黃國忠.“大概念”推動課堂變化 凸顯數學育人價值［J］.教學教法，2022（1）：78-80.

［2］中華人民共和國教育部.義務教育數學課程標準（2022年版）［M］.北京：人民教育出版社，2022.

［3］藍藝明.“雙減”政策下小學數學精準教學案例分析——以“認識鐘表”教學為例［J］.教育科學論壇，2022（1）：8-11.

責任編輯：趙瀟晗