非線性俘能系統機電耦合動力學模型分析及故障診斷應用研究

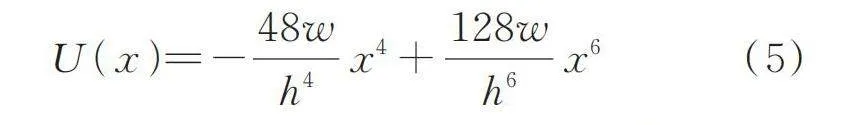
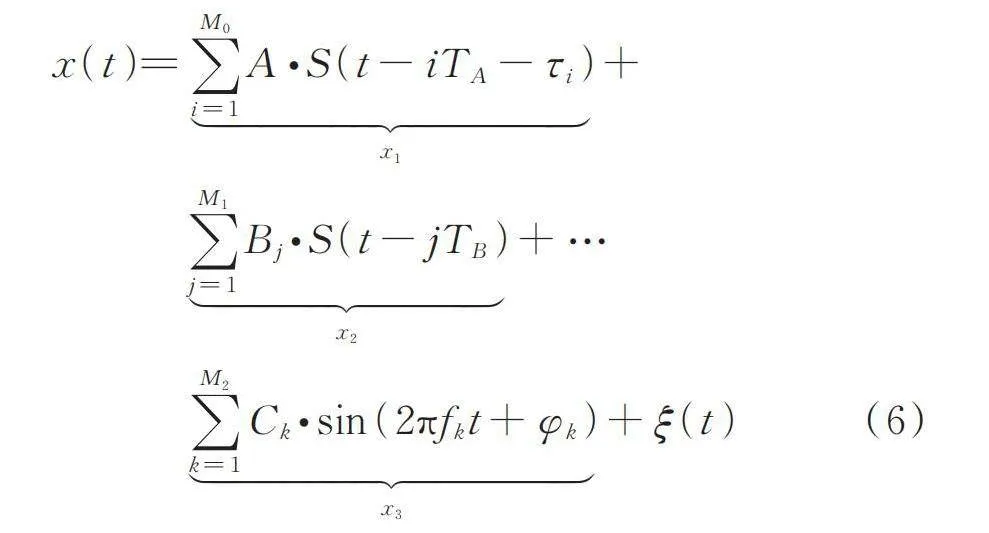
摘要： 研究勢阱參數對非線性俘能系統輸出特性的影響有利于設計高性能的俘能系統；同時，俘能系統對應的機電耦合動力學模型中的隨機共振現象可用于增強微弱故障特征，進而有效識別微弱故障。本文提出一種解耦的鞍點退化雙穩態勢能函數，并基于此勢能函數介紹了機電耦合動力學模型。研究了在不同激勵幅值下位移響應的分岔圖，分析了勢阱寬度與勢阱高度對系統響應（包括周期響應與混沌響應）的影響。選取固定的激勵幅值，利用龐加萊映射（Poincaré Map）、頻譜分析（Frequency Spectrum Analysis）以及李雅普諾夫指數（Lyapunov Exponent）等方法分別驗證系統發生了周期響應與混沌響應，驗證結果與分岔圖相吻合。基于受隨機噪聲擾動的非線性俘能系統機電耦合動力學模型，提出了基于此模型隨機共振的故障診斷方法，實現了對軸承故障特征增強的目的。

關鍵詞： 非線性系統； 能量俘獲； 故障診斷； 李雅普諾夫指數； 龐加萊映射

中圖分類號： O322； TM619； TH165+.3 文獻標志碼： A 文章編號： 1004-4523（2024）10-1714-09

DOI：10.16385/j.cnki.issn.1004-4523.2024.10.009

引 言

隨著無線傳感技術的快速發展，微型低功耗傳感器已廣泛應用于人體健康監測［1］、重大機械設備的結構健康監測系統［2］，以及軌道交通基礎設施狀態監測系統等［3?4］。但傳統的微型傳感器大部分需要化學電池供能，這種供能形式需要定期更換電池，且更換的電池對環境有害。利用能量俘獲技術俘獲環境中的風能［5?6］、海洋能［7?8］以及低頻振動能量［9?10］等綠色能源可實現對微型低功耗傳感器的長期供能。針對不同的激勵形式，研究學者分別研究了基礎激勵、氣動激勵、旋轉激勵以及隨機激勵等的振動能量俘獲系統（簡稱“俘能系統”）。Zhou等［11］推導了基礎激勵下非對稱三穩態俘能系統的諧波平衡解，揭示了其中的非線性動力學機制。Huang等［12］利用諧波平衡法獲得了基礎激勵下非對稱四穩態俘能系統的理論解，并分析了不同的勢阱深度對阱間振動的影響。Tai等［13］推導了基礎激勵下基于最大功率的優化條件。Li等［14］利用增量諧波平衡法理論分析了三穩態顫振式俘能系統的周期解和分岔，并通過風洞試驗進行了驗證。Huang等［15］利用復變量平均法理論推導了馳振和基礎激勵下俘能系統的理論解，并分析了其動力學性能。Hou等［16］研究了在渦激振動和基礎激勵下的壓電?電磁混合俘能系統。相比單一渦激振動或單一基礎激勵下的俘能系統，俘獲的能量功率得到了提高。Mei等［17］提出了具有時變特征的四穩態俘能系統，用于俘獲低頻旋轉能量。在旋轉運動下，俘能系統的有效工作頻率范圍為1～7 Hz。Wang等［18］研究了旋轉環境下梯形梁俘能系統。與矩形梁相比，在夾具附近，梯形梁可以承受更高的應力。Fang等［19］利用膨脹的離心軟化效應提出了超低頻旋轉運動下的俘能系統，其功率密度為41.23 μW/g。

非線性系統隨機共振現象已廣泛應用于工程領域［20］，如圖像增強［21?22］、能量俘獲［23?24］以及故障診斷［25?26］。其原理是：在合適強度噪聲干擾下，非線性系統會發生隨機共振，使系統輸出幅值達到最大。Kim等［27］利用自調節隨機共振的優點，提出了一種用于調制噪聲激勵下旋轉運動的能量俘獲系統。與其他用于輪胎的俘能系統相比，該系統具有更大的功率輸出和有效帶寬。Gong等［28］研究了多穩態俘能系統的隨機共振現象，用于增強在隨機旋轉激勵下的能量俘獲性能。Shi等［29］基于改進的非對稱隨機共振模型，闡述了如何利用噪聲使系統發生隨機共振進而改進俘能系統能量俘獲效率。同樣地，隨機共振現象在故障診斷領域也有重要的應用。Lai等［30］基于雙穩態Duffing系統，提出了一種尺度變換方法，可以將隨機共振方法應用于大參數信號。Lei等［31］基于穩態匹配的欠阻尼隨機共振方法，實現了滾動體軸承的早期故障診斷。此方法能夠通過優化尺度因子抑制多尺度噪聲的干擾。張剛等［32］研究了二維雙阱勢系統隨機共振機理，并將其用于實際工業軸承故障診斷，提高了故障頻率處峰值的辨識度。賀利芳等［33］提出了高斯勢分段雙穩隨機共振系統，分別研究了在高斯白噪聲和有色噪聲下衡量指標隨系統參數的變化規律。

非線性俘能系統具有復雜的機電耦合動力學響應，如果能把其中的隨機共振現象應用于故障診斷領域，既能擴大俘能系統的應用范圍，又能豐富基于隨機共振的機械裝備故障診斷方法。因此，本文也探索了非線性俘能系統機電耦合動力學模型隨機共振現象在故障診斷中的潛在應用。

1 無量綱動力學模型

Yang等［34］研究發現非線性退化（鞍點退化與中心點退化）可以使非線性系統在超低頻或低隨機激勵強度下實現大幅值的阱間振蕩，可有效提高低激勵水平下的能量俘獲性能。因此，本節首先基于鞍點退化雙穩態勢能函數研究退化勢能函數的勢阱寬度與勢阱高度對壓電俘能系統響應的影響。其對應的無量綱機電耦合方程［35］可寫為：

（1）

（2）

式中 表示系統位移響應；表示系統輸出電壓；表示無量綱的等效電容；表示無量綱的等效機電耦合系數； 表示無量綱的等效電阻；表示無量綱的等效阻尼； 表示無量綱的基礎激勵幅值；表示無量綱的基礎激勵的角頻率。若俘能系統為對稱雙穩態系統，則無量綱的非線性力可表示為：

（3）

令式（3）等于零，則其對應有一個零根，兩個虛根和兩個實根。而若將式（3）中的項去除，則新的將對應有三個零根，兩個實根。在文獻［34］中，這種具有三個零根，兩個實根的對應的勢能函數稱為鞍點退化勢能函數。此時，可表示為［34］：

（4）

式中 表示非線性力系數；表示退化雙穩態勢能函數的穩定平衡點；表示勢能函數對求導。因此，鞍點退化勢能函數的勢阱寬度，勢阱高度。

對鞍點退化勢能函數進行解耦，可得關于勢阱寬度與勢阱高度的解耦勢能函數：

（5）

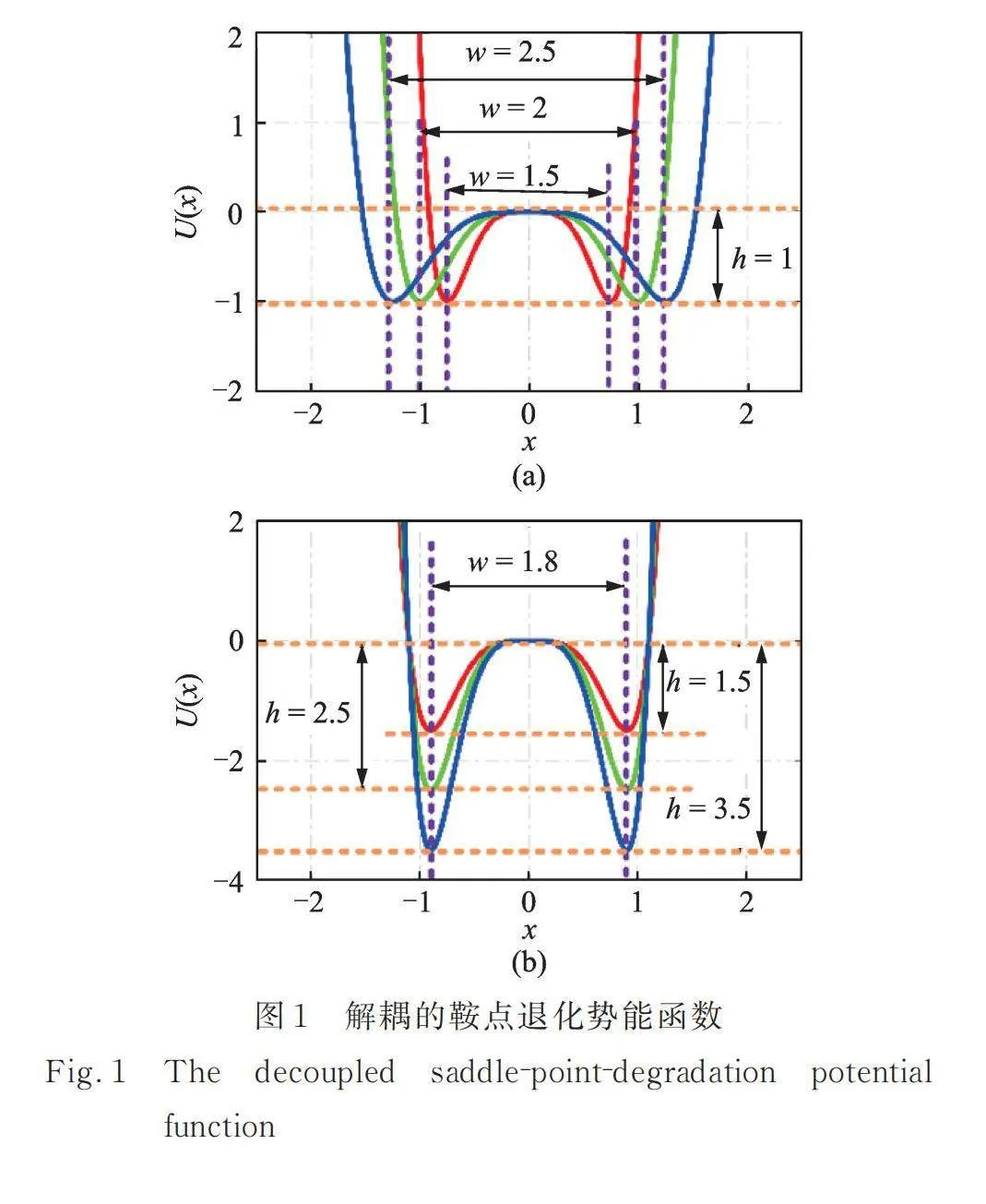
如圖1所示，解耦的鞍點退化勢能函數可由勢阱寬度或勢阱高度獨立控制，即當勢阱寬度變化時，可以保證勢阱高度不變；勢阱高度變化時，可以保證勢阱寬度不變。這方便研究勢阱寬度與勢阱高度對非線性俘能系統的影響。

2 數值分析

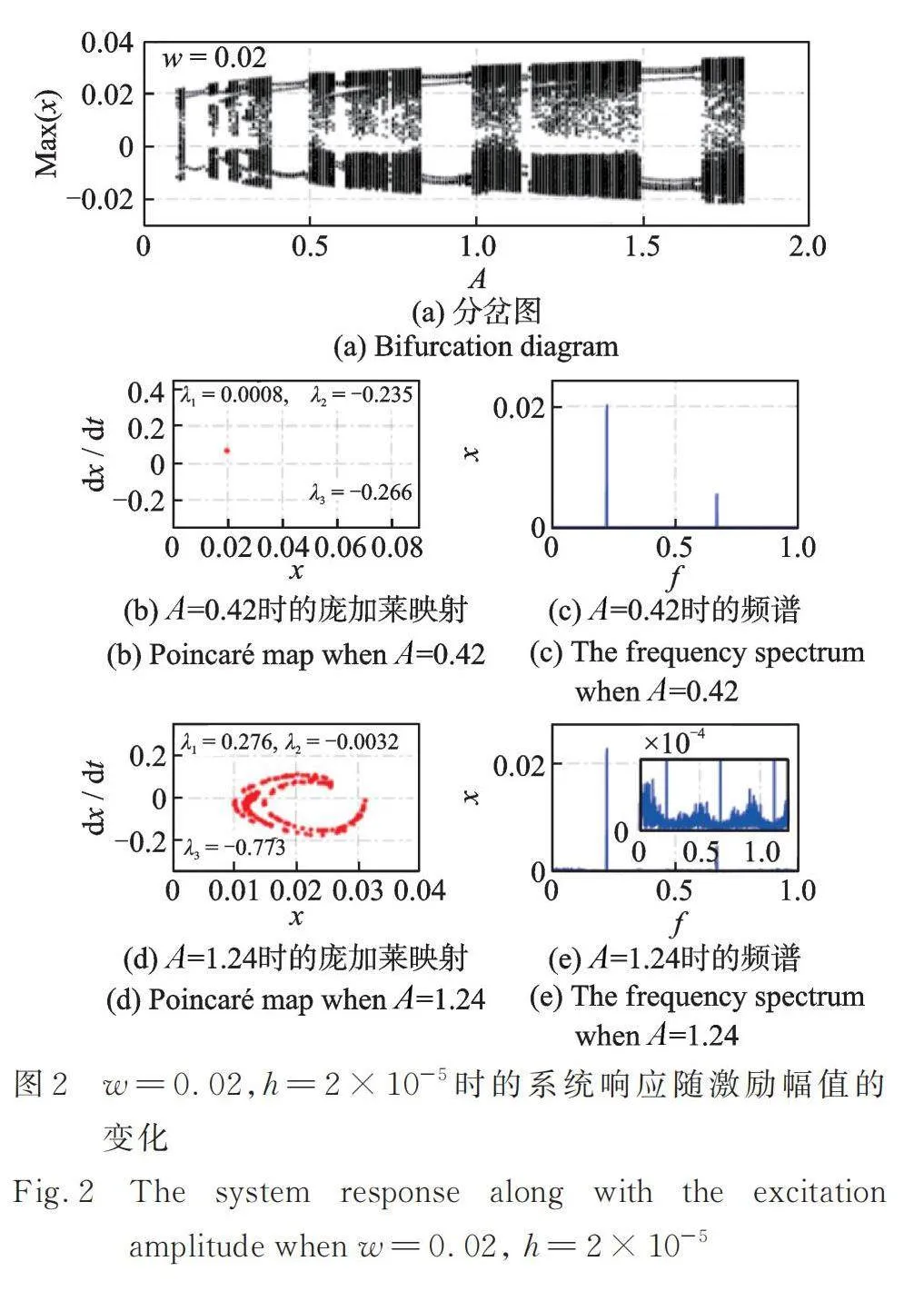
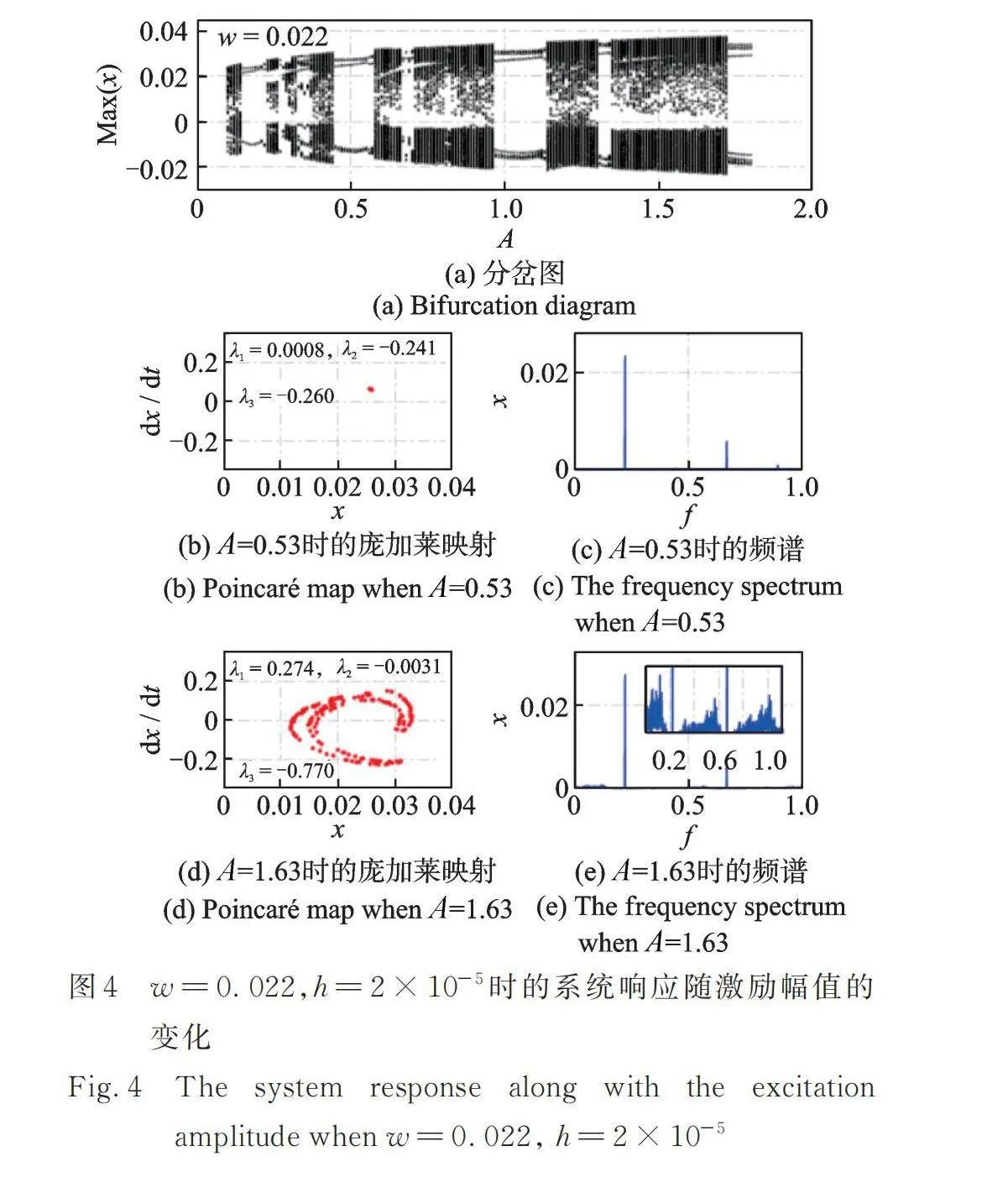
本節利用分岔圖［36?37］（分岔圖是計算不同參數下穩定位移響應的幅值而獲得的幅值分布圖）研究了勢阱寬度與勢阱高度對系統響應（周期響應與混沌響應）的影響，可進一步反向指導特定激勵強度下具有周期響應的俘能系統的結構設計。在數值分析過程中，無量綱激勵幅值以0.01的步距從0.1變化到1.8，其他的無量綱參數分別為：，，，，。圖2～8展示了不同勢阱寬度與勢阱高度下的分岔圖、龐加萊映射（Poincaré Map）、頻譜圖以及李雅普諾夫指數（Lyapunov Exponent，本文的機電耦合系統對應有三個李雅普諾夫指數，分別表示為：，，）。

2.1 勢阱寬度對系統響應的影響

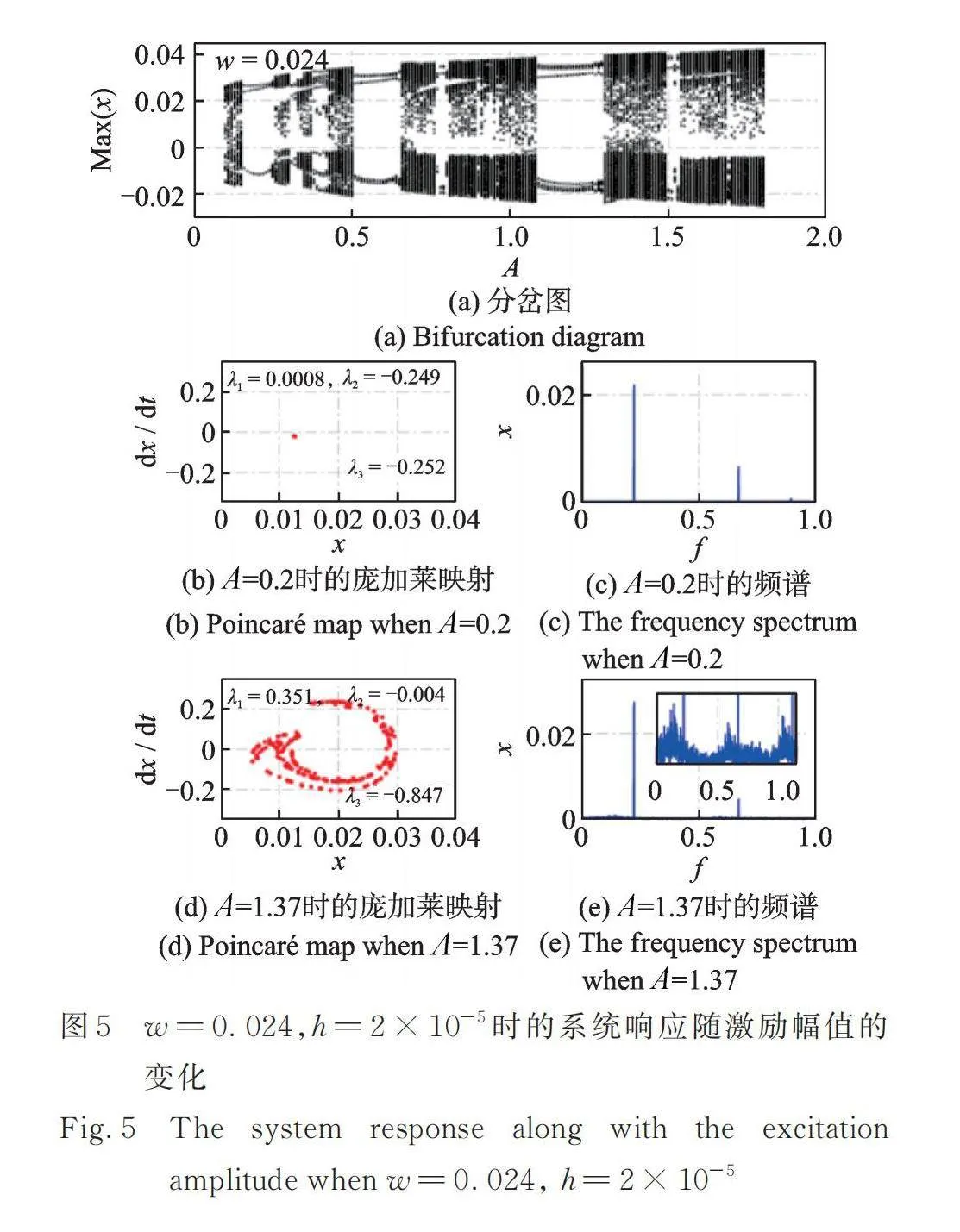
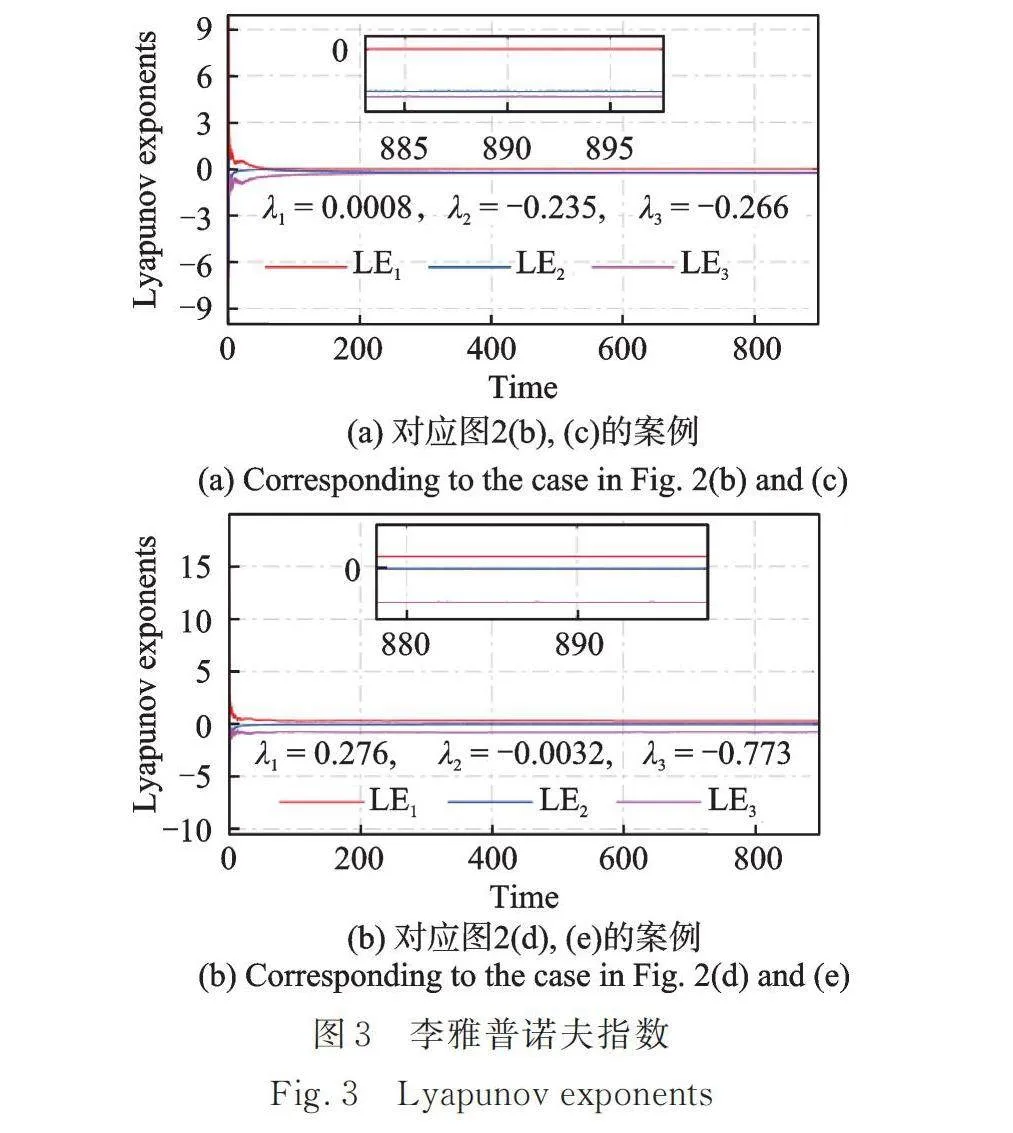
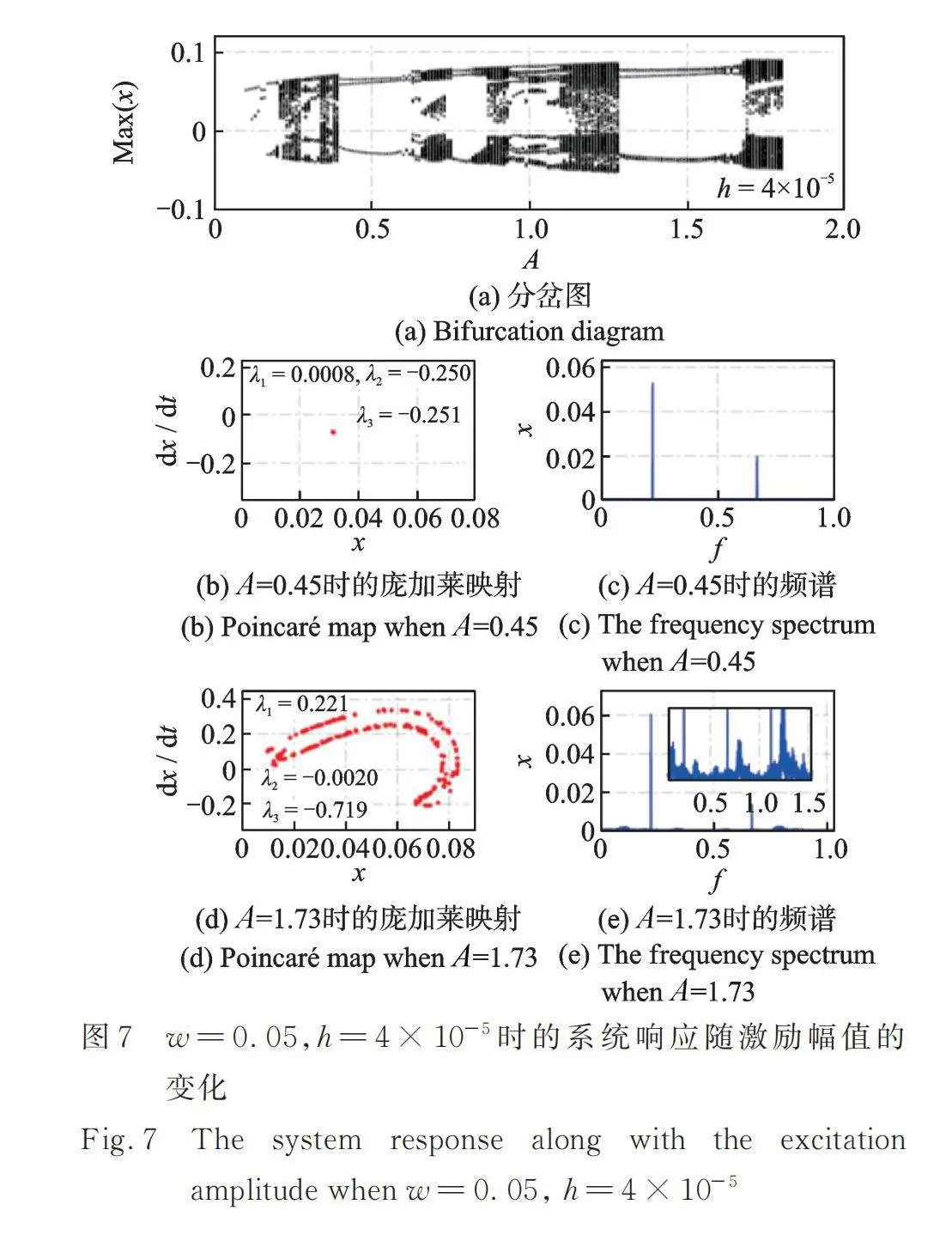
圖2～5展示了當勢阱高度時，不同勢阱寬度下非線性俘能系統響應隨激勵幅值的變化。其中，圖3詳細展示了圖2中李雅普諾夫指數隨時間的變化趨勢（其他圖中的最終李雅普諾夫指數值已在圖中標明）。從圖2，4和圖5中可以看出，隨著勢阱寬度的增大，非線性俘能系統發生混沌響應的區域將會整體朝著激勵幅值增大的方向移動。在低激勵幅值處的混沌區域將會變大。在特定的激勵幅值下，系統發生周期響應時，其龐加萊映射為單個點，頻譜中僅有明顯的單頻及其倍頻成分，最大的李雅普諾夫指數［38?39］（）約為0。當系統發生混沌響應時，其龐加萊映射具有明顯的軌跡，頻譜呈現明顯的多頻成分，最大李雅普諾夫指數大于0［38?39］。

2.2 勢阱高度對系統響應的影響

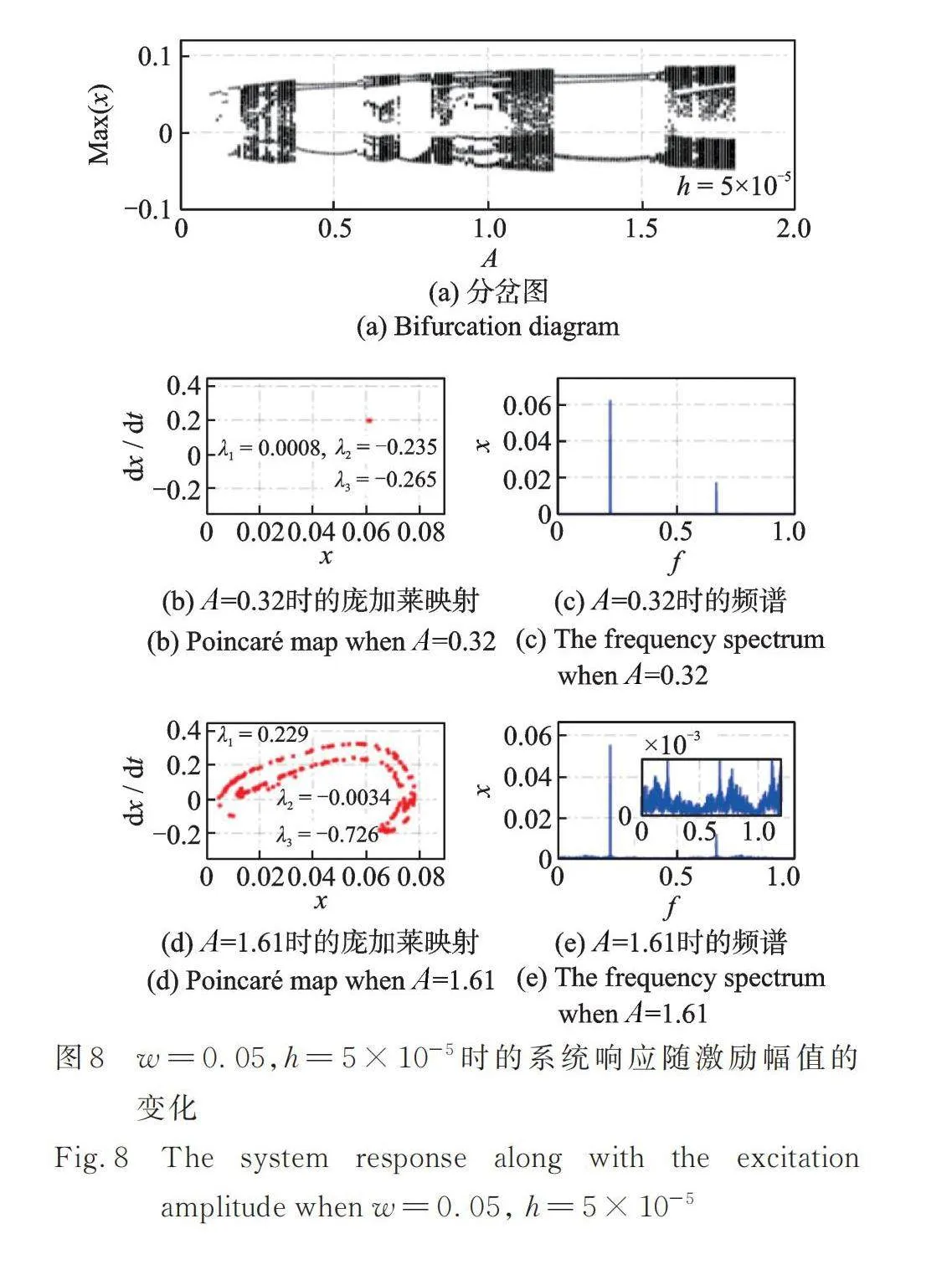
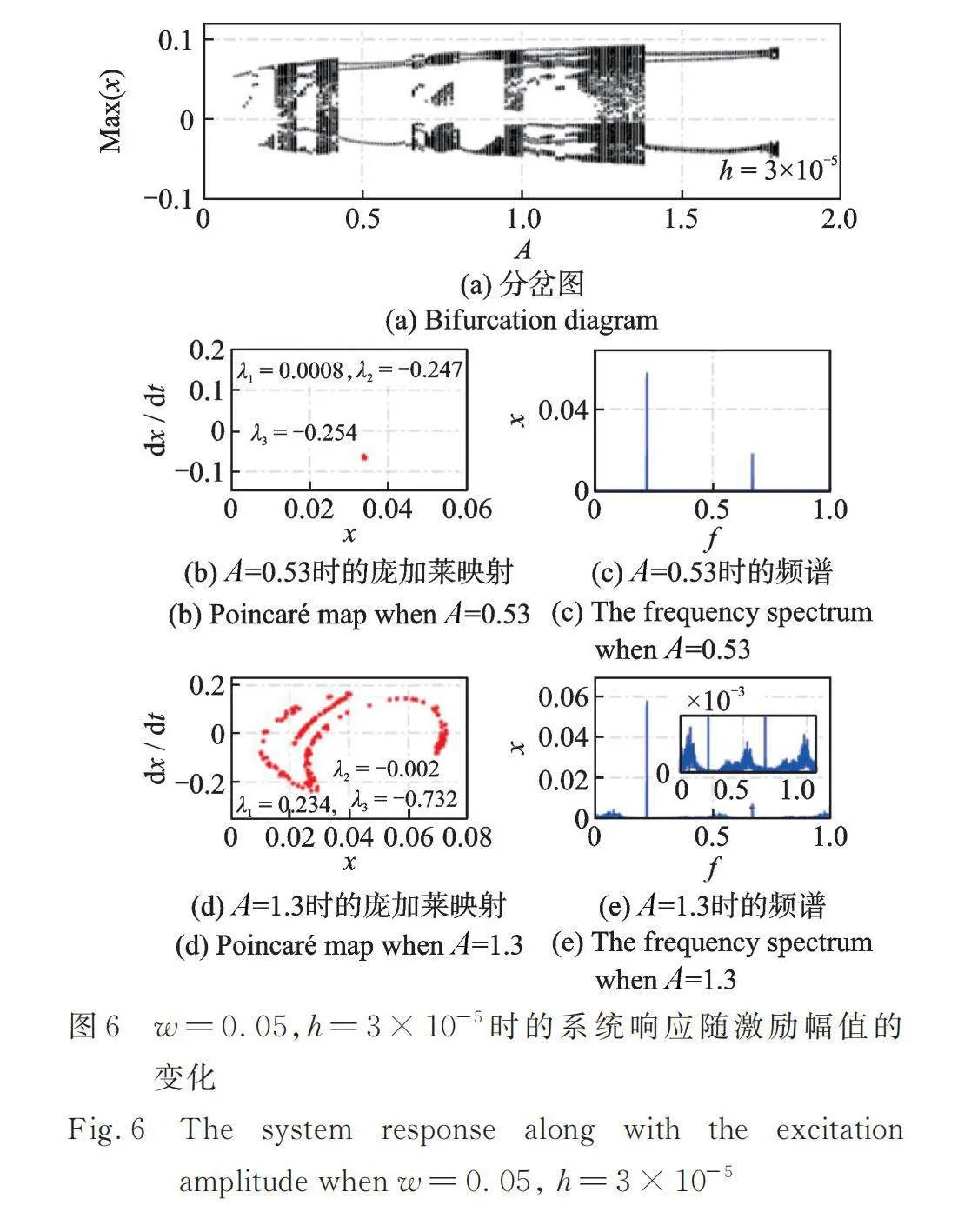
圖6～8展示了當勢阱寬度時，不同勢阱高度下非線性俘能系統響應隨激勵幅值的變化。同樣地，在取固定的激勵幅值時，其對應的龐加萊映射、頻譜圖以及李雅普諾夫指數均能夠證明系統是周期響應或是混沌響應，進一步說明了分岔圖的準確性。此外，從圖中可知，在保證勢阱寬度不變的條件下增大勢阱高度，在分岔圖中體現的混沌區域將會整體朝著激勵幅值減小的方向移動。在高激勵幅值處的混沌區域將會增大。

3 在故障診斷中的應用

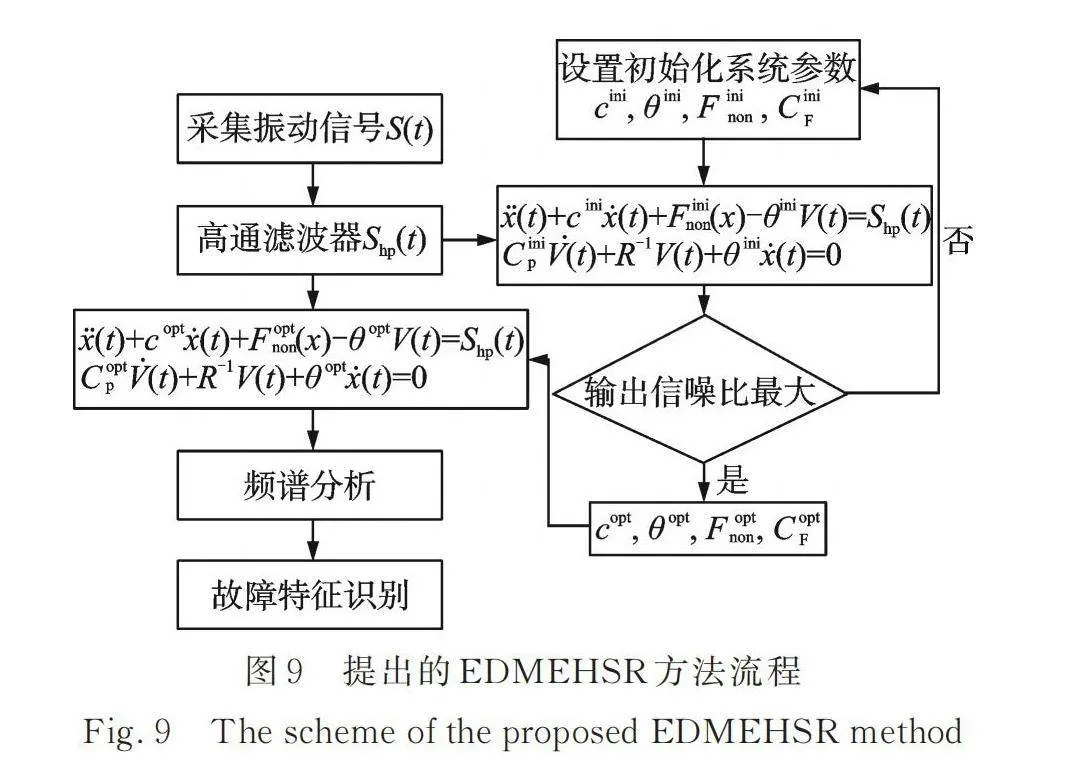
非線性系統的隨機共振現象已成功應用于增強俘能系統的輸出性能［27?29］，本節探索機電耦合動力學模型俘能系統的隨機共振現象（Stochastic Resonance Phenomenon of the Electromechanical Dynamic Model of the Energy Harvester，EDMEHSR）在故障診斷領域中的應用。如圖9所示，EDMEHSR方法的主要流程為：步驟1，獲得采集信號的包絡信號；步驟2，對包絡信號進行高通濾波（去除低頻成分）；步驟3，輸入到機電耦合方程（1）和（2），利用龍格?庫塔方法獲得輸出信號；步驟4，計算輸出信噪比；步驟5，重復步驟1～4，記錄輸出信噪比最大時的系統參數以及輸出信號。

3.1 仿真驗證

為了驗證提出的EDMEHSR方法的有效性，將其應用到仿真的軸承內圈和軸承外圈故障信號中。仿真信號模型如下式所示［40］：

（6）

式中 第一項表示周期成分，第二項表示隨機脈沖成分，第三項表示干擾諧波成分，第四項表示加性白噪聲。可表示為：

（7）

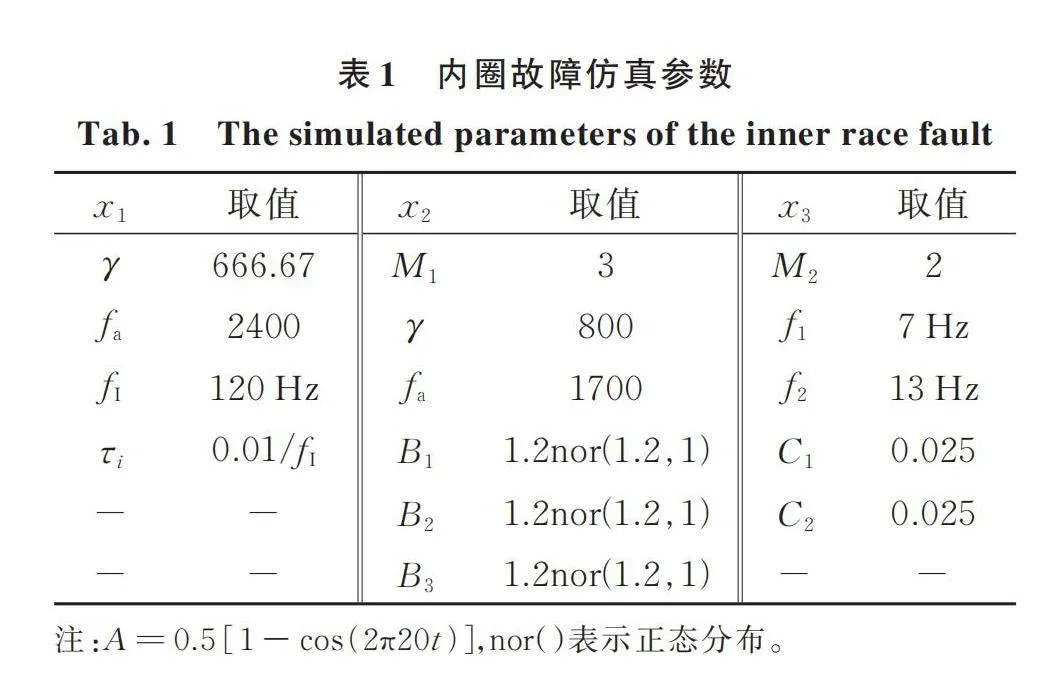
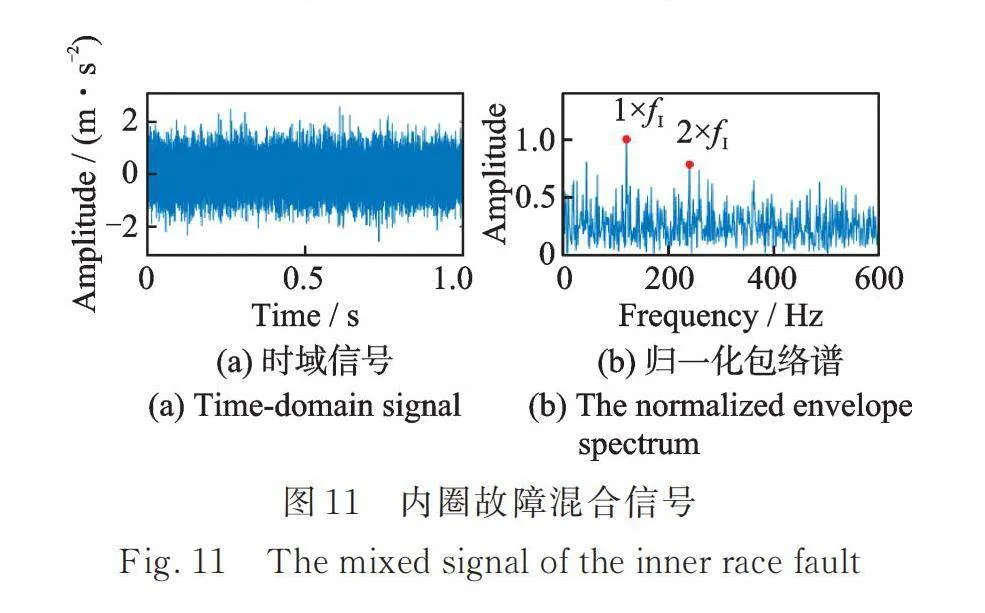
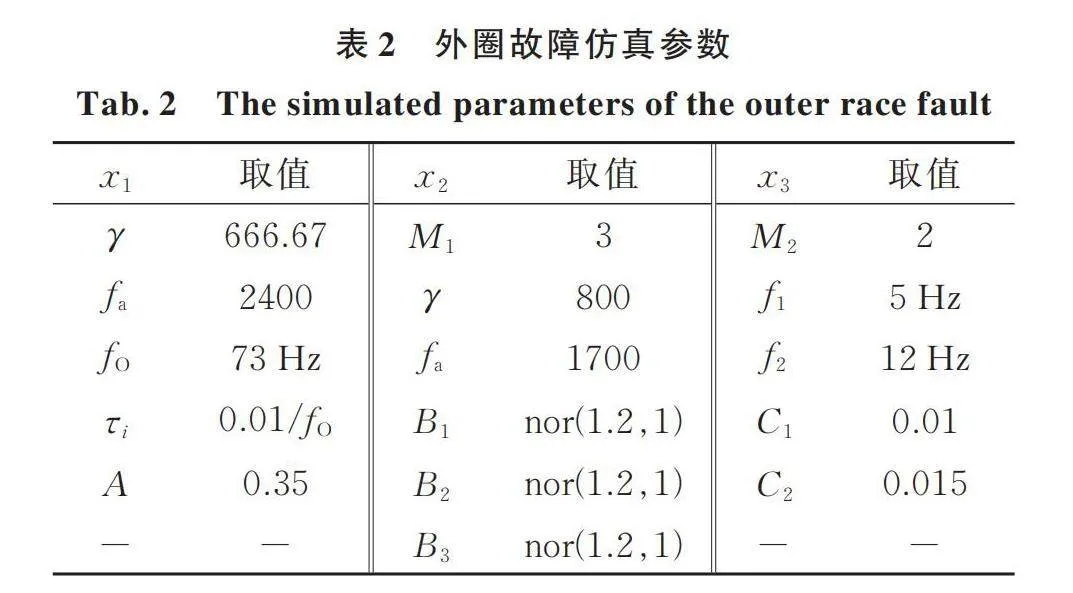
仿真參數如表1和2所示，仿真的軸承外圈故障頻率（Ball Pass Frequency of Outer Race，）為73Hz，內圈故障頻率（Ball Pass Frequency of Inner Race，）為120 Hz。

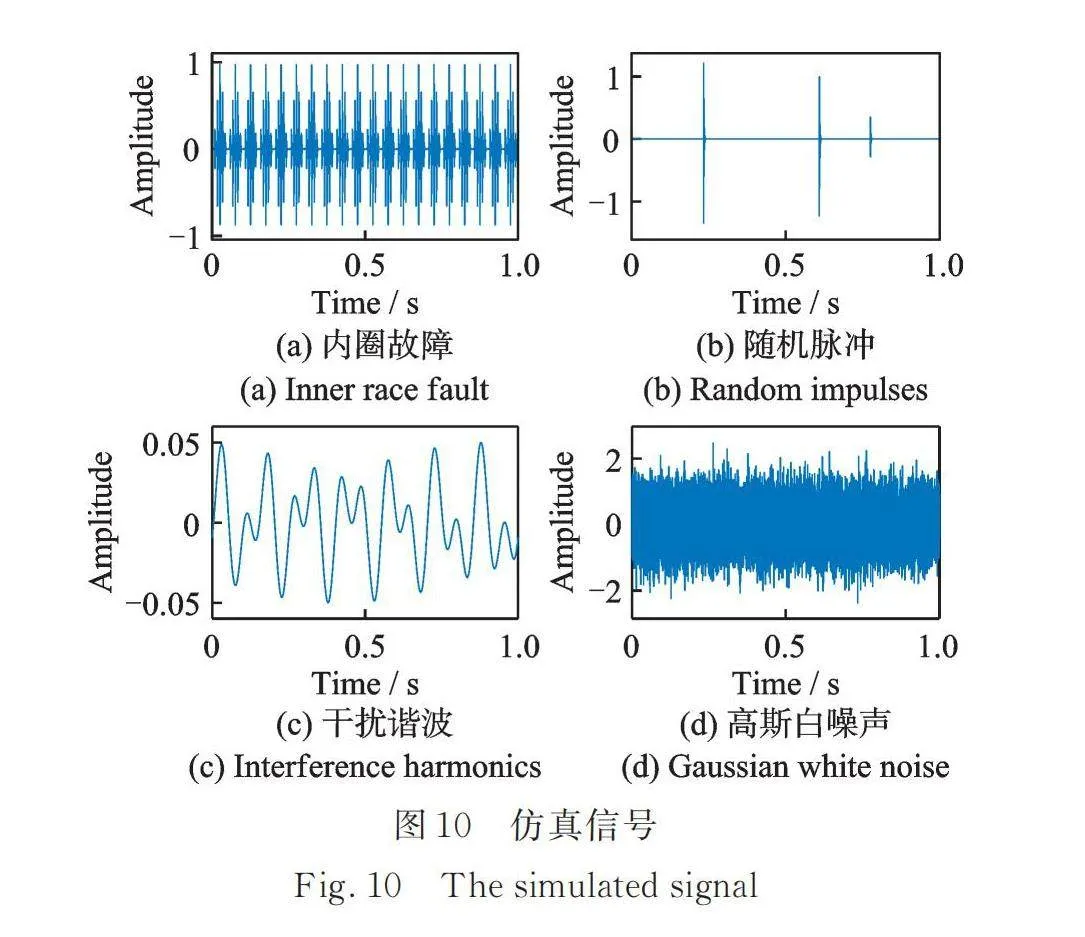
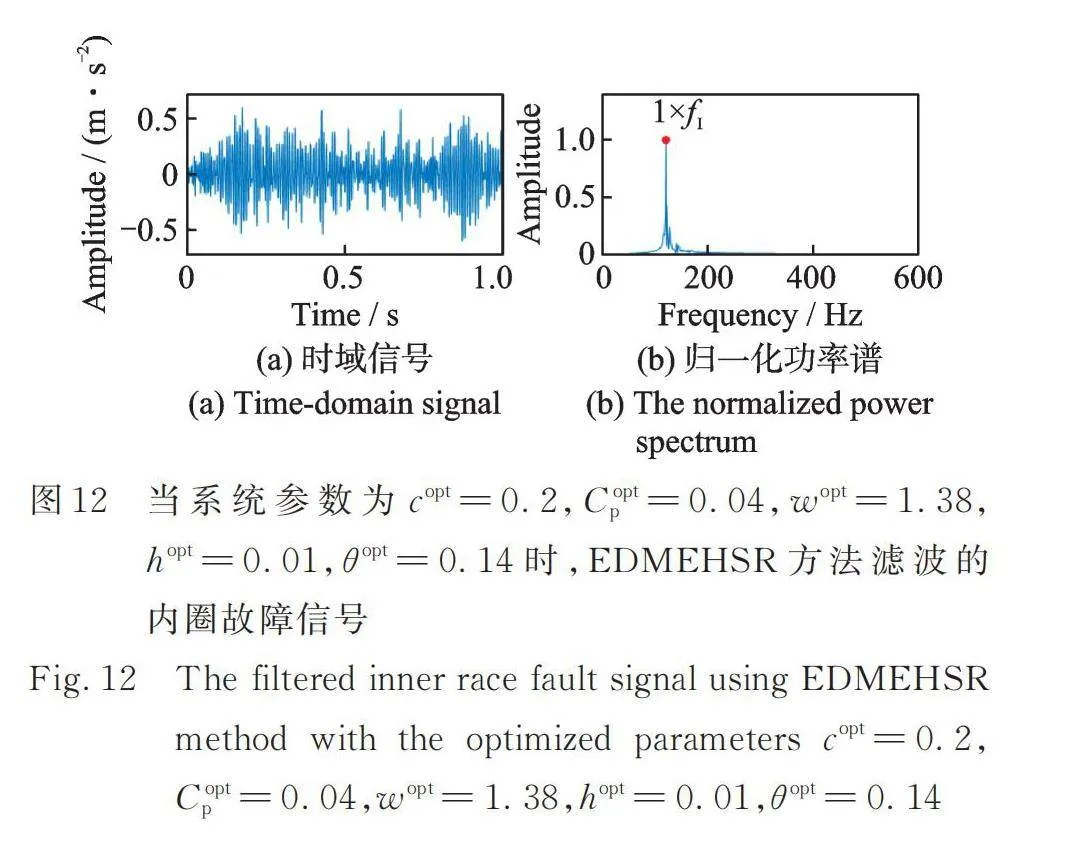
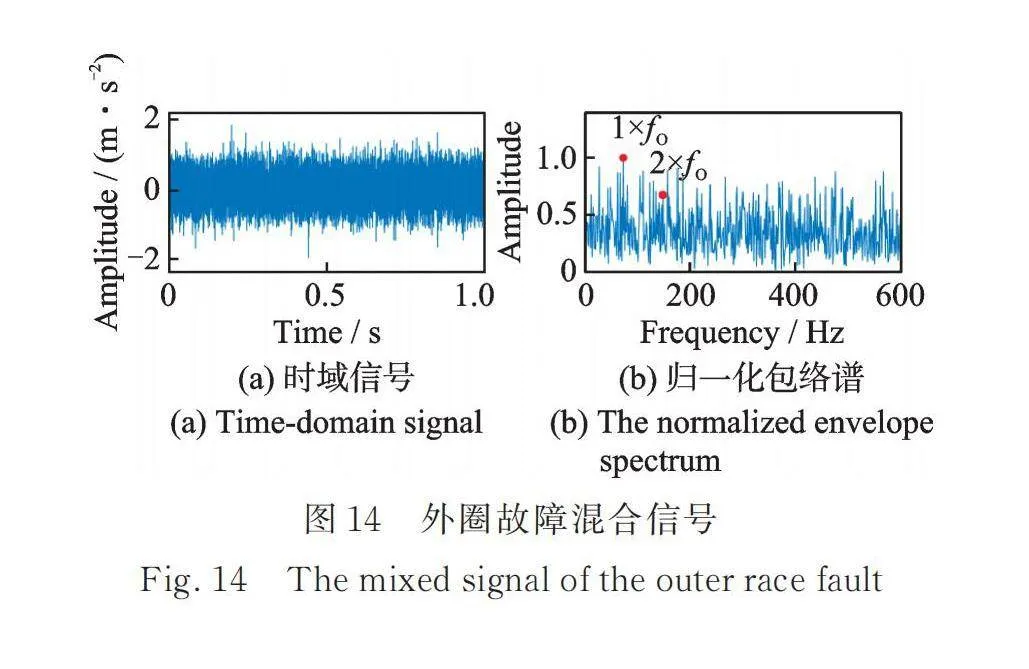
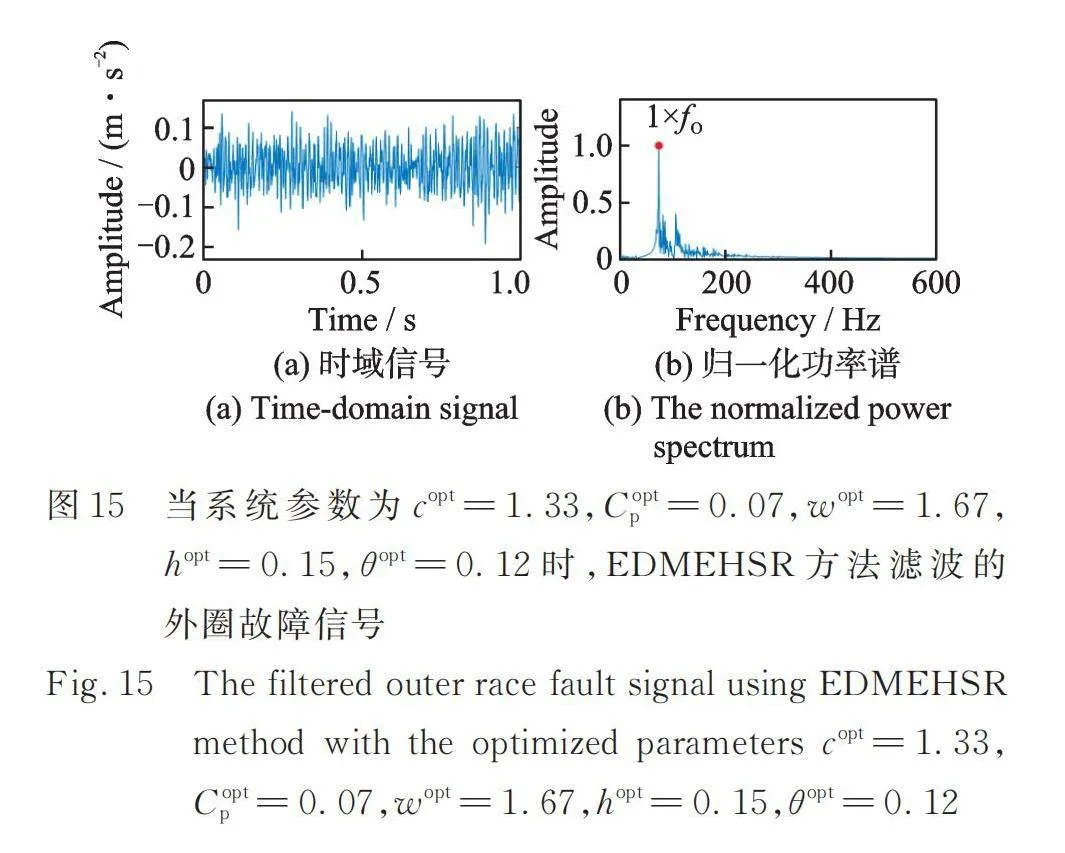
如圖10與13所示，仿真的信號成分分別為內圈、外圈的周期脈沖信號、隨機脈沖、干擾諧波以及高斯白噪聲。仿真內圈混合信號及其歸一化包絡譜和仿真的外圈混合信號及其歸一化包絡譜分別如圖11和14所示。在其對應的歸一化包絡譜中，故障特征頻率處的幅值受噪聲影響很大。應用EDMEHSR方法后（如圖12與15所示），仿真的故障特征頻率處的幅值得到增強，遠遠大于其他頻率處的幅值。圖11，12，14和15頻譜對應的信噪比如表3所示，基于EDMEHSR方法可獲得最高的信噪比輸出信號。綜上，這兩個仿真案例有效證明了EDMEHSR方法的有效性和其增強目標信號的能力。

3.2 實驗驗證

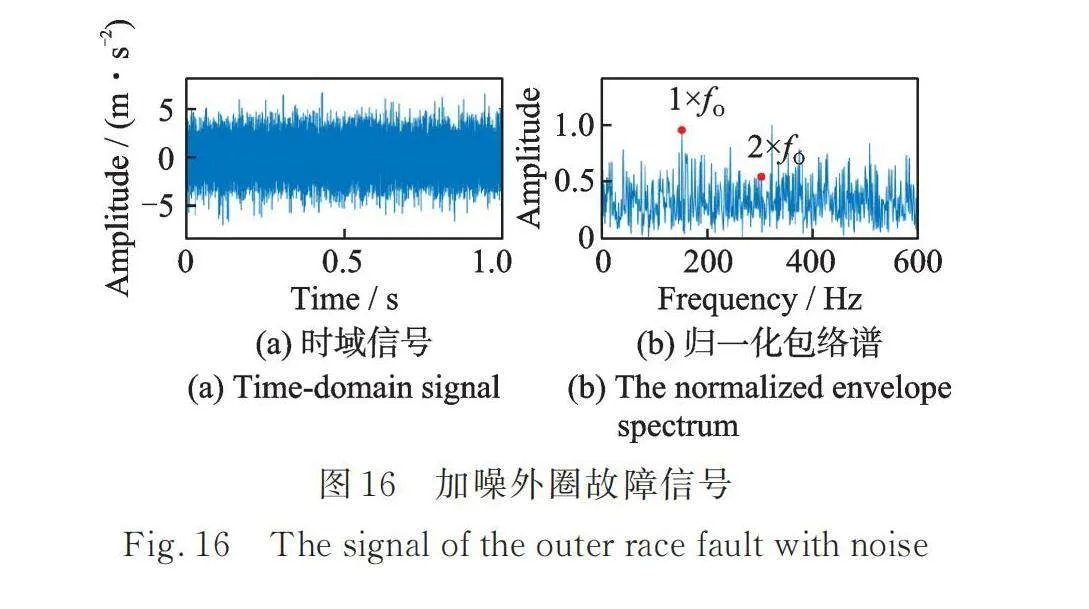
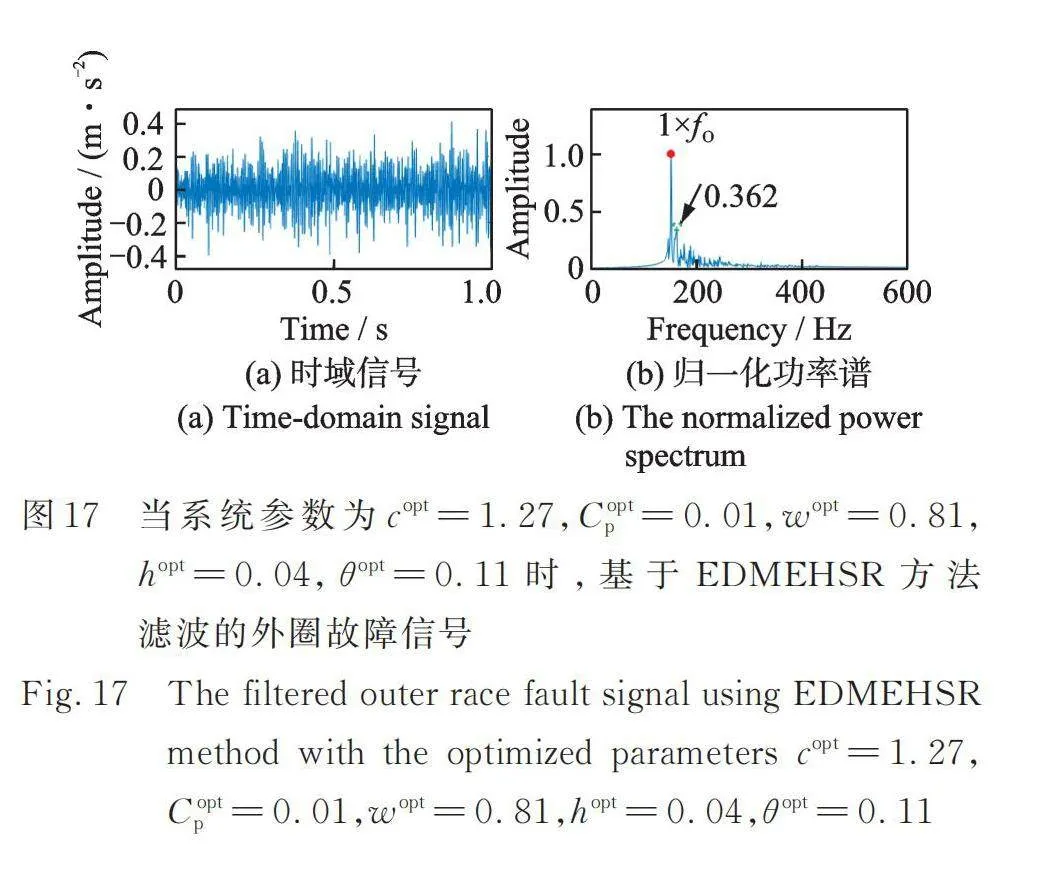
本節利用軸承外圈故障實驗數據進一步驗證本文提出的EDMEHSR方法的有效性。圖16展示了加噪的軸承外圈故障實驗信號及其歸一化包絡譜。圖16（b）對應的SNR為-33.9489 dB，且從圖中可觀測到外圈故障特征頻率的峰值幾乎被噪聲成分淹沒。圖17展示了利用優化參數的EDMEHSR方法獲得的濾波信號及其歸一化功率譜，優化參數為：，，，，。圖17（b）對應的SNR為-15.3597 dB，且從圖中可明顯觀測到外圈故障特征頻率，指示軸承的外圈發生故障。此外，對比輸出信號SNR可知，基于EDMEHSR的方法極大提高了故障特征頻率處的信噪比。

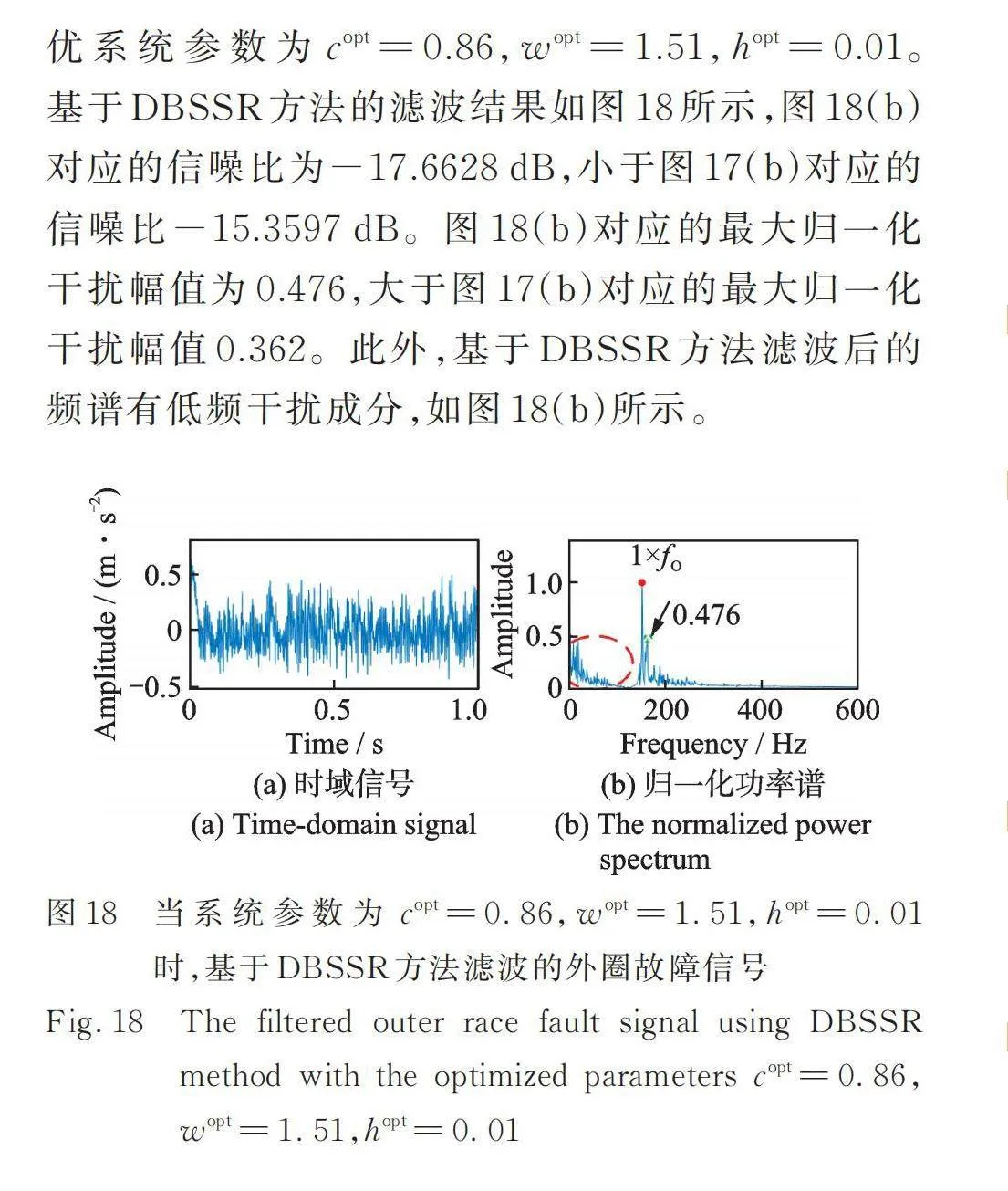
本節還將式（1）對應的解耦雙穩態系統（不包含電壓項）的隨機共振現象（Stochastic Resonance Phenomenon of the Decoupled Bistable System，DBSSR）用于故障診斷，算法流程與圖9展示的相同。以信噪比為優化指標，獲得DBSSR方法的最優系統參數為，，。基于DBSSR方法的濾波結果如圖18所示，圖18（b）對應的信噪比為-17.6628 dB，小于圖17（b）對應的信噪比-15.3597 dB。圖18（b）對應的最大歸一化干擾幅值為0.476，大于圖17（b）對應的最大歸一化干擾幅值0.362。此外，基于DBSSR方法濾波后的頻譜有低頻干擾成分，如圖18（b）所示。

綜上，在相同優化流程的情況下，基于機電耦合系統的隨機共振現象的故障診斷方法獲得的濾波信號具有信噪比高，受干擾小的優點。

4 結 論

本文建立了基于解耦的鞍點退化勢能函數的機電耦合動力學模型，數值分析了不同激勵幅值下非線性俘能系統的輸出響應（周期響應與混沌響應），為非線性俘能系統的結構設計提供參考。最后實現了非線性俘能系統機電耦合動力學模型隨機共振現象在故障診斷中的應用。本文主要結論如下：

勢阱高度對系統的影響與勢阱寬度產生的影響完全相反。增大勢阱寬度將使非線性俘能系統發生混沌響應的區域向著大激勵幅值方向移動，且在低激勵幅值處的混沌區域將會增大。因此在設計具有周期響應特征的非線性俘能系統時，可根據環境激勵幅值等級，選取合適的勢阱高度與勢阱寬度值。

此外，仿真與實驗軸承故障案例表明，基于機電耦合動力學模型俘能系統隨機共振現象的方法可有效增強故障特征，濾除噪聲干擾。這展示了一種非線性能量俘獲系統作為非線性濾波器在故障診斷中的潛在工程應用。

參考文獻：

［1］楊濤，周生喜，曹慶杰，等. 非線性振動能量俘獲技術的若干進展［J］. 力學學報，2021，53（11）： 2894?2909.

Yang Tao，Zhou Shengxi，Cao Qingjie，et al. Some advances in nonlinear vibration energy harvesting technology［J］. Chinese Journal of Theoretical and Applied Mechanics，2021，53（11）： 2894?2909.

［2］Zhang Y，Wu X，Lei Y G，et al. Self?powered wireless condition monitoring for rotating machinery［J］. IEEE Internet Things Journal，2023，11（2）： 3095?3107.

［3］高鳴源，王平. 磁浮式軌道振動俘能機理與試驗研究［J］. 鐵道學報，2018，40（6）： 144?153.

Gao Mingyuan，Wang Ping. Harvesting railroad vibration energy by magnetic levitation oscillation［J］. Journal of the China Railway Society，2018，40（6）： 144?153.

［4］Cao H，Kong L J，Tang M F，et al. An electromagnetic energy harvester for applications in a high?speed rail pavement system［J］. International Journal of Mechanical Sciences，2023，243： 108018.

［5］李支援，呂文博，馬小青，等. 一種磁力滑動式翼型顫振能量俘獲器［J］. 力學學報，2023，55（10）： 2146?2155.

Li Zhiyuan，Lü Wenbo，Ma Xiaoqing，et al. A magnetic sliding airfoil flutter energy harvester［J］. Chinese Journal of Theoretical and Applied Mechanics，2023，55（10）： 2146?2155.

［6］Wang J L，Zhou S X，Zhang Z E，et al. High-performance piezoelectric wind energy harvester with Y-shaped attachments［J］. Energy Conversion and Management，2019，181： 645?652.

［7］Xie X D，Wang Q. A study on an ocean wave energy harvester made of a composite piezoelectric buoy structure［J］. Composite Structures，2017，178： 447?454.

［8］Liu R W，He L P，Liu X J，et al. A review of collecting ocean wave energy based on piezoelectric energy harvester［J］. Sustainable Energy Technologies and Assessments，2023，59： 103417.

［9］Mitcheson P D，Yeatman E M，Rao G K，et al. Energy harvesting from human and machine motion for wireless electronic devices［J］. Proceedings of the IEEE，2008，96（9）： 1457?1486.

［10］Yang Z B，Zhou S X，Zu J，et al. High?performance piezoelectric energy harvesters and their applications［J］. Joule，2018，2（4）： 642?697.

［11］Zhou S X，Zuo L. Nonlinear dynamic analysis of asymmetric tristable energy harvesters for enhanced energy harvesting［J］. Communications in Nonlinear Science and Numerical Simulation，2018，61： 271?284.

［12］Huang D M，Han J L，Zhou S X，et al. Stochastic and deterministic responses of an asymmetric quad?stable energy harvester［J］. Mechanical Systems and Signal Processing，2022，168： 108672.

［13］Tai W C，Zuo L. On optimization of energy harvesting from base?excited vibration［J］. Journal of Sound and Vibration，2017，411： 47?59.

［14］Li Z Y，Zhou S Z，Zhang H，et al. Periodic solutions and bifurcations of a tristable flutter?based energy harvester［J］. Aerospace Science and Technology，2024，144： 108815.

［15］Huang D M，Han J L，Li W，et al. Responses，optimization and prediction of energy harvesters under galloping and base excitations［J］. Communications in Nonlinear Science and Numerical Simulation，2023，119： 107086.

［16］Hou C W，Li C H，Shan X B，et al. A broadband piezo?electromagnetic hybrid energy harvester under combined vortex?induced and base excitations［J］. Mechanical Systems and Signal Processing，2022，171： 108963.

［17］Mei X T，Zhou S X，Yang Z C，et al. Enhancing energy harvesting in low?frequency rotational motion by a quad?stable energy harvester with time?varying potential wells［J］. Mechanical Systems and Signal Processing，2021，148： 107167.

［18］Wang J X，Su W B，Li J C，et al. A rotational piezoelectric energy harvester based on trapezoid beam： simulation and experiment［J］. Renewable Energy，2022，184： 619?626.

［19］Fang S T，Chen K Y，Lai Z H，et al. Analysis and experiment of auxetic centrifugal softening impact energy harvesting from ultra?low?frequency rotational excitations［J］. Applied Energy，2023，331： 120355.

［20］靳艷飛，許鵬飛，李永歌，等. 多穩態動力系統中隨機共振的研究進展［J］. 力學進展，2023，53（2）： 357?394.

Jin Yanfei，Xu Pengfei，Li Yongge，et al. Stochastic resonance of multi?stable dynamical systems： a review［J］. Advances in Mechanics，2023，53（2）： 357?394.

［21］Kojima N，Lamsal B，Matsumoto N. An adaptive tuning stochastic resonance approach for image enhancement on illumination variant images［J］. Journal of the Institute of Industrial Applications Engineers，2017，5（1）： 24?31.

［22］Jiao S B，Shi J Q，Wang Y，et al. A novel image noise reduction method for composite multistable stochastic resonance systems［J］. Heliyon，2023，9（3）： e14431.

［23］McInnes C R，Gorman D G，Cartmell M P. Enhanced vibrational energy harvesting using nonlinear stochastic resonance［J］. Journal of Sound and Vibration，2008，318（4?5）： 655?662.

［24］Zhang Y S，Zheng R C，Shimono K，et al. Effectiveness testing of a piezoelectric energy harvester for an automobile wheel using stochastic resonance［J］. Sensors，2016，16（10）： 1727.

［25］Xu H T，Zhou S X. Periodicity?assist double delay-controlled stochastic resonance for the fault detection of bearings［J］. Measurement，2024，225： 114018.

［26］Xu H T，Zhou S X，Yang T. Stochastic resonance of a high?order?degradation bistable system and its application in fault diagnosis with variable speed condition［J］. Mechanical Systems and Signal Processing，2023，186： 109852.

［27］Kim H，Tai W，Parker J，et al. Self?tuning stochastic resonance energy harvesting for rotating systems under modulated noise and its application to smart tires［J］. Mechanical Systems and Signal Processing，2019，122： 769?785.

［28］Gong X L，Xu P F，Liu D，et al. Stochastic resonance of multi?stable energy harvesting system with high?order stiffness from rotational environment［J］. Chaos，Solitons and Fractals，2023，172： 113534.

［29］Shi P M，Liu Z X，Li M D，et al. Nonlinear dynamics analysis of enhancing energy harvesting from intense vibration based on improved asymmetric bistable stochastic resonance model［J］. Chinese Journal of Physics，2023，90：223?236.

［30］Lai Z H，Leng Y G. Weak?signal detection based on the stochastic resonance of bistable Duffing oscillator and its application in incipient fault diagnosis［J］. Mechanical Systems and Signal Processing，2016，81： 60?74.

［31］Lei Y G，Qiao Z J，Xu X F，et al. An underdamped stochastic resonance method with stable?state matching for incipient fault diagnosis of rolling element bearings［J］. Mechanical Systems and Signal Processing，2017，94： 148?164.

［32］張剛，徐浩，張天騏. 二維雙阱勢系統隨機共振機理研究及應用［J］. 振動與沖擊，2021，40（12）： 15?22.

Zhang Gang，Xu Hao，Zhang Tianqi. A study and application of stochastic resonance mechanism in a two-dimensional bistable potential system［J］. Journal of Vibration and Shock，2021，40（12）： 15?22.

［33］賀利芳，劉秋玲，張剛. 高斯勢分段雙穩隨機共振在不同噪聲下的軸承故障診斷［J］. 振動與沖擊，2023，42（3）： 30?42.

He Lifang，Liu Qiuling，Zhang Gang. Bearing fault diagnosis under different noises with GPPBSR system［J］. Journal of Vibration and Shock，2023，42（3）： 30?42.

［34］Yang T，Xu H T，Tang J，et al. Exploring nonlinear degradation benefit of bio?inspired oscillator for engineering applications［J］. Applied Mathematical Modelling，2023，119： 736?762.

［35］Zhou S X，Cao J Y，Lin J. Theoretical analysis and experimental verification for improving energy harvesting performance of nonlinear monostable energy harvesters［J］. Nonlinear Dynamics，2016，86（3）： 1599?1611.

［36］Moysis L，Lawnik M，Volos C. Density?colored bifurcation diagrams?a complementary tool for chaotic map analysis［J］. International Journal of Bifurcation and Chaos，2023，33（15）： 2330036.

［37］Moysis L，Giakoumis A，Gupta M K，et al. Observers for rectangular descriptor systems with output nonlinearities： application to secure communications and microcontroller implementation［J］. International Journal of Dynamics and Control，2021，9（2）： 530?540.

［38］李海濤，丁虎，陳立群. 帶有非對稱勢能阱特性的雙穩態能量采集系統混沌動力學分析［J］. 振動與沖擊，2020，39（18）： 54?59.

Li Haitao，Ding Hu，Chen Liqun. Chaotic dynamics of a bi?stable energy harvesting system with asymmetric potential well characteristics［J］. Journal of Vibration and Shock，2020，39（18）： 54?59.

［39］Li H，Shen Y J，Han Y J，et al. Determining Lyapunov exponents of fractional?order systems： a general method based on memory principle［J］. Chaos，Solitons and Fractals，2023，168： 113167.

［40］Miao Y H，Zhao M，Lin J，et al. Application of an improved maximum correlated kurtosis deconvolution method for fault diagnosis of rolling element bearings［J］. Mechanical Systems and Signal Processing，2017，92： 173?195.

Analysis and fault diagnosis application of the electromechanical dynamic model of the nonlinear energy harvester

XU Hai?tao，ZHOU Sheng?xi

（School of Aeronautics，Northwestern Polytechnical University，Xi’an 710072，China）

Abstract： The study of the influence of potential well parameters on the output of a nonlinear energy harvester system is conducive to the design of the high-performance energy harvester system. Meanwhile，the stochastic resonance phenomenon in the corresponding electromechanical coupling dynamics model of the energy harvester system can be used to enhance the characteristics of weak faults，so as to effectively identify weak faults. This paper proposes a decoupled saddle-point-degradation bistable potential function，and the electromechanical dynamic model is introduced. The bifurcation diagram under different excitation amplitudes is obtained to discuss the effect of the barrier width and the barrier height on the responses （periodic response and chaotic response）. According to the methods of the Poincaré map，the frequency spectrum analysis，and the Lyapunov exponent，the periodic response and the chaotic response are examined at a fixed excitation amplitude，which is consistent with that obtained from the bifurcation diagram. Based on the electromechanical dynamic model perturbed by the random noise，the stochastic-resonance-based method is proposed for fault diagnosis，which achieves the enhancement of the simulated and experimental bearing fault characteristics.

Key words： nonlinear system；energy harvesting；fault diagnosis；Lyapunov exponent；Poincaré map

作者簡介： 徐海濤（1993―），男，博士研究生。E?mail： xuhaitao@mail.nwpu.edu.cn。

通訊作者： 周生喜（1987―），男，博士，教授。E?mail： zhoushengxi@nwpu.edu.cn。