柔性機械臂干擾力觀測與無模型振動控制

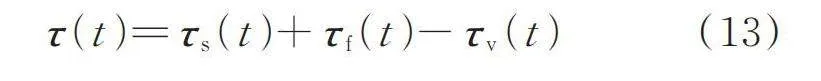
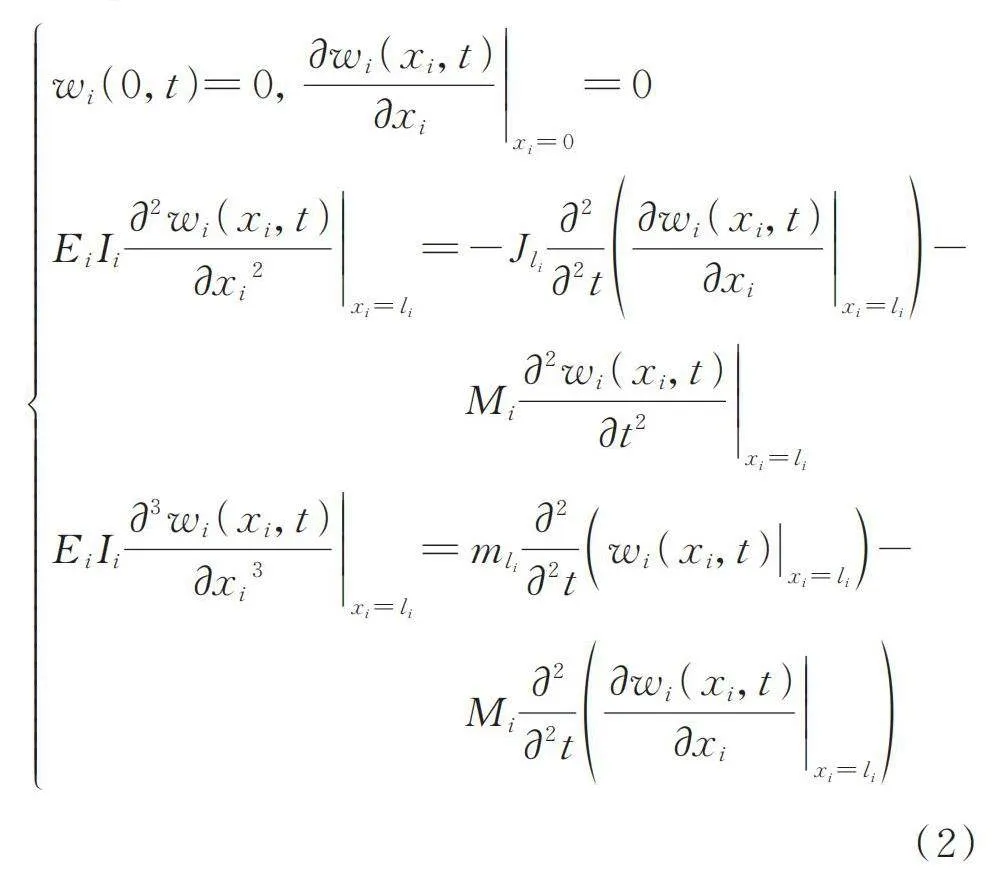
摘要： 為了抑制柔性機械臂運動過程中的非線性振動，提出一種基于干擾力在線觀測的無模型軌跡跟蹤和振動抑制混合控制策略。采用拉格朗日方程和奇異攝動法對存在未知干擾的柔性機械臂進行動力學建模和解耦，將其分解為表征剛性運動的慢變子系統和表征柔性振動的快變子系統；考慮到建模的復雜性和模型參數的不確定性，采用PD控制方法實現軌跡跟蹤，并提出無模型自適應控制算法以實現柔性臂桿的非線性振動控制。針對未知外界干擾可能引起的控制發散問題，提出了改進的干擾力狀態觀測器，用于干擾力矩的在線估計和實時補償，有效提高無模型振動控制算法的收斂性能。仿真試驗結果表明，所提算法在存在干擾力的情況下對柔性機械臂的振動抑制效果顯著，且具有良好的動態性能和魯棒性。

關鍵詞： 柔性機械臂； 振動控制； 無模型自適應控制； 干擾觀測器

中圖分類號： O313.7； TB535 文獻標志碼： A 文章編號： 1004-4523（2024）10-1783-09

DOI：10.16385/j.cnki.issn.1004-4523.2024.10.017

引 言

柔性機械臂具有結構輕、負載比高、能耗低等優點，被廣泛應用于工業、軍事、航空航天等領域［1?2］。然而，由于其剛度低、阻尼小，在運動過程中易產生低頻振動，嚴重影響了機械臂的定位精度和運動穩定性［3?4］。柔性機械臂振動控制可分為反饋控制和前饋控制兩大類［5］。前饋控制的優點是不需要反饋傳感器，但其本質屬于開環控制技術，在處理各種干擾和參數變化方面存在局限性。反饋控制充分利用關節和柔性臂桿振動狀態信息，具有較強的抗外界干擾能力，可實現穩定控制。傳統反饋振動控制方法大多需要獲得柔性機械臂精確的模型參數，即模型類反饋控制。然而，由于末端負載變化、關節非線性摩擦、臂桿柔性等不確定及非線性因素，柔性機械臂的精確模型參數難以獲得。為了克服這個問題，滑模控制［6］、魯棒控制［7］、神經網絡控制［8?9］、模糊控制［10?11］等智能控制方法陸續被提出，以解決模型參數獲取困難的問題。但這些算法存在計算量大、實時性差等問題。

無模型控制是一種數據驅動型控制，不需要被控對象的物理模型參數，只需要系統的輸入和輸出數據。當被控系統結構參數時變或不確定時，無模型控制可以避免結構參數辨識，提高控制效率。PID控制和迭代學習控制［12］是相對成熟且應用廣泛的無模型控制方法。近年來，無模型自適應控制（Model Free Adaptive Control，MFAC）［13?14］因其僅依靠輸入/輸出數據即能夠實現未知非線性系統的自適應控制而備受關注。然而，直接將MFAC算法應用于柔性機械臂控制存在一些挑戰。MFAC算法需要實時輸入/輸出數據，對數據質量要求極高，尤其是在數據出現突變的情況下適應能力較差。在機械臂遭遇干擾或碰撞時，控制力會出現劇烈波動，從而導致系統穩定時間延長，嚴重時甚至可能導致控制系統崩潰。未知外界干擾無法直接測得或測量代價太高。一般情況下，通過設計狀態觀測器來利用可測量狀態估計系統外部干擾，并通過反饋擾動估計提高系統的魯棒性。Liu等［15］利用降階擴展狀態觀測器，設計自抗擾控制算法，實現永磁同步電動機電流控制。Shang等［16］提出了一種采用非線性擾動觀測器的自適應PI控制策略，實現柔性機械臂的振動抑制。可見，通過干擾觀測器進行外部干擾估計，是解決未知外界擾動對MFAC控制算法的影響的可行方案。

綜上所述，柔性機械臂的精確建模難度較大，模型參數獲取不易，且在控制過程中容易受到各種干擾。因此，本文提出了一種基于擴張狀態觀測器（Extended State Observer，ESO）的無模型混合控制方法。該方法無需系統精確模型參數，通過無模型PD和MFAC控制算法進行混合控制，實現柔性機械臂軌跡跟蹤和振動控制。針對未知外界干擾，提出改進型擴張狀態觀測器（Modified Extended State Observer，MESO）對干擾力矩進行在線估計和實時補償，有效提高柔性機械臂無模型振動控制算法的收斂性能。

1 柔性機械臂動力學

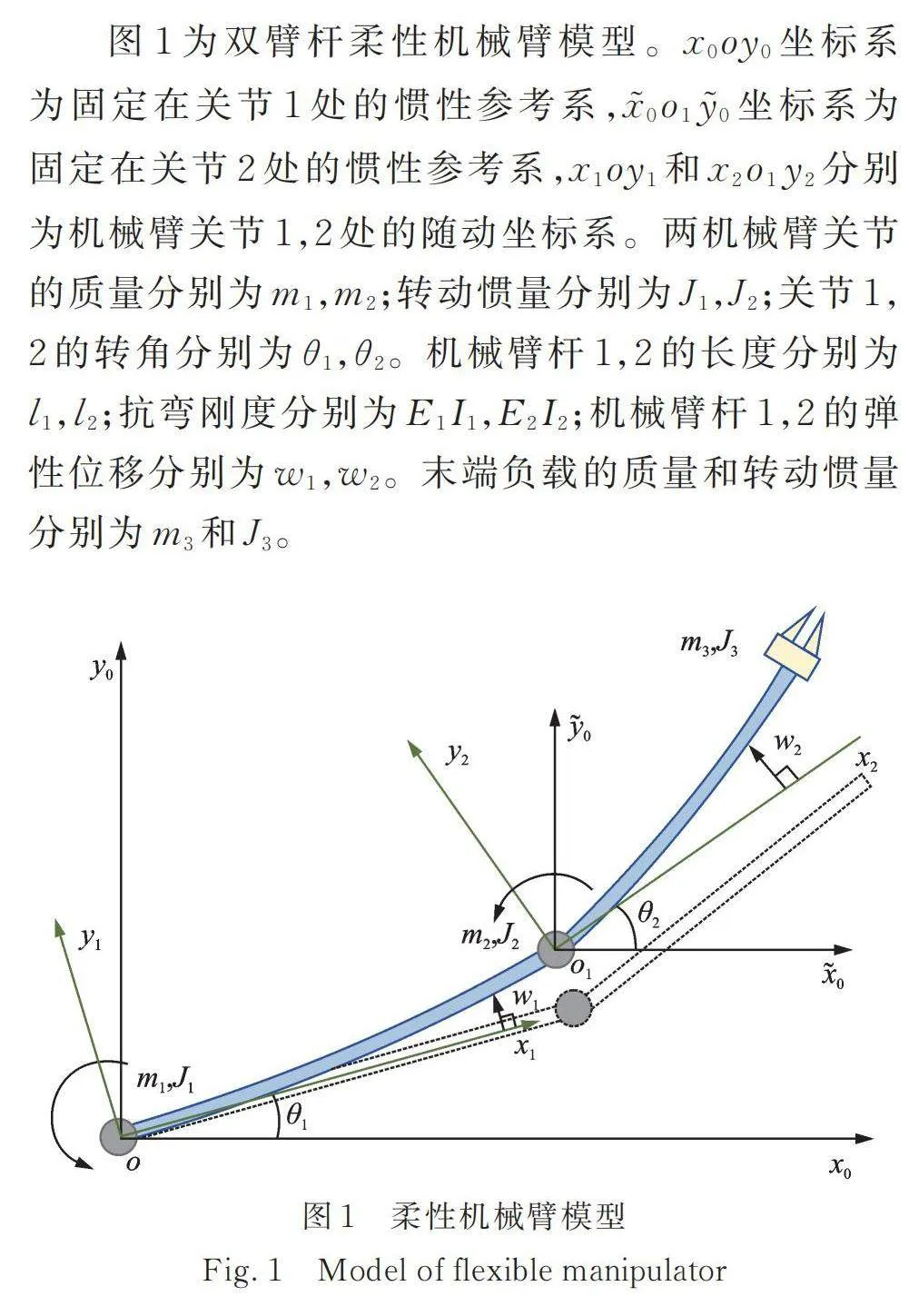
圖1為雙臂桿柔性機械臂模型。坐標系為固定在關節1處的慣性參考系，坐標系為固定在關節2處的慣性參考系，和分別為機械臂關節1，2處的隨動坐標系。兩機械臂關節的質量分別為，；轉動慣量分別為，；關節1，2的轉角分別為，。機械臂桿1，2的長度分別為，；抗彎剛度分別為，；機械臂桿1，2的彈性位移分別為，。末端負載的質量和轉動慣量分別為和。

1.1 柔性機械臂的動力學建模

當柔性臂桿滿足小變形假設時，忽略柔性臂的軸向變形與剪切變形，可將其視為Euler?Bernoulli梁，采用假設模態法，柔性機械臂桿的橫向撓度為：

（1）

式中 為柔性臂桿的橫向撓度；為第i號臂桿的第j階振型，為對應的模態坐標；s為模態截斷階數。

假設關節剛度較大，柔性臂振動主要取決于柔性臂的結構參數，故將柔性臂桿根部近似為固定邊界條件。由于柔性臂末端帶有負載，自由振動時梁的自由端內力不再為零。假設和為柔性臂桿i的末端轉動慣量和質量，為柔性臂桿i+1轉動產生的偏移量對質量的影響。則柔性臂i末端的剪應力和彎矩分別由，和決定［17］，機械臂桿的邊界條件為：

（2）

由于柔性機械臂的低階振動模態占主導地位，高階振動模態的貢獻可以忽略［18］，故本文取2階模態截斷。定義為柔性機械臂轉角向量，為描述柔性機械臂彈性振動的模態坐標向量，利用拉格朗日方程可以推導出柔性機械臂動力學方程為：

（3）

式中 ，，，組成了慣性矩陣；為剛度矩陣的組成部分；，，為包含了科式力和離心力的向量；為關節控制驅動力矩；為外部干擾力。

1.2 動力學方程的奇異攝動分解

基于動力學方程狀態變量在時間尺度上的差異，采用奇異攝動法將柔性機械臂動力學系統分解為兩個低階系統。首先，忽略快變變化現象，得到簡化解。穩態結果表示在系統中起主導作用的緩慢變化現象。然后在“拉伸”時間尺度上計算邊界層校正項，進行誤差校正和補償。

從系統的動力學特性上來看，其質量矩陣是正定對稱的，因此質量矩陣M存在逆矩陣N為：

（4）

方程（3）兩邊左乘矩陣N，動力學方程改寫為：

（5）

為了導出系統奇異攝動方程的標準形式，需要引入奇異攝動尺度因子，為一個很小的正參數。由于與動力學方程中其他矩陣元素相比，剛度矩陣中的元素具有較大的數量級，令，其中為剛度矩陣中的元素。令，并定義奇異攝動尺度下新的變量為：

（6）

將式（6）代入式（5），動力學方程可改寫為奇異攝動模型：

（7）

令，則式（7）可以化簡為：

（8）

（9）

從式（9）中解出并代入式（8），適當簡化方程中符號，可得機械臂慢變子系統的動力學方程為：

（10）

式中 =，和分別為慢變子系統的驅動力矩和干擾力。

對于快變子系統，引入邊界層校正變量：

（11）

式中 為慢變子系統中的值，在快變尺度下可以被視為常數。

在邊界層上引入快變時標，可寫出快變子系統的動力學方程為：

（12）

式中 ，為慢變子系統中的慣性矩陣相應子矩陣；和分別為慢變子系統的電機驅動力矩和干擾力。

通過奇異攝動法，將柔性機械臂的動力學方程分解為慢變子系統和快變子系統的動力學方程，分別如式（10）和（12）所示。可以看出，慢變子系統在大時間范圍內代表剛性運動，快變子系統在小時間范圍內代表彈性振動。

2 柔性機械臂的混合控制策略

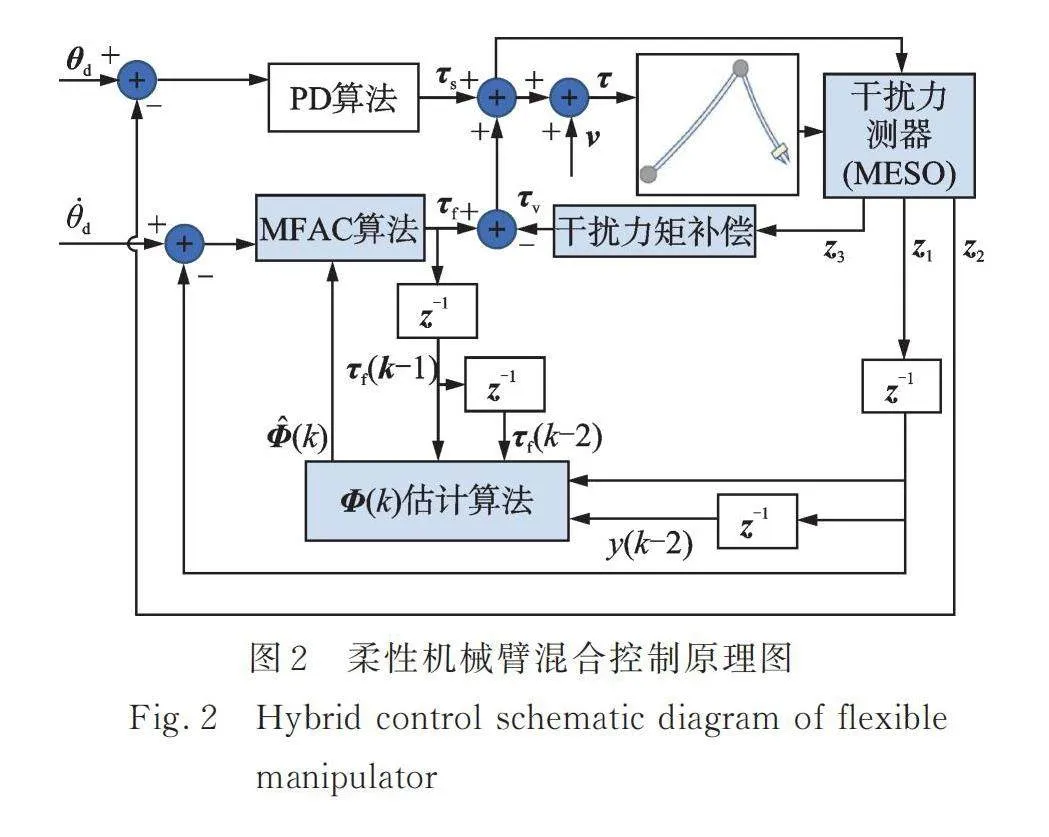
基于1.2節中得到的動力學方程（10）和（12），并考慮到柔性機械臂的精確模型參數無法獲取，本節提出一種柔性機械臂軌跡跟蹤和振動抑制無模型混合控制策略。混合控制原理圖如圖2所示。

控制系統由3部分組成：第1部分采用PD反饋控制，計算慢變子系統控制力矩，實現軌跡跟蹤；第2部分設計抑制柔性機械臂振動的MFAC算法，計算快變子系統控制力矩；第3部分設計MESO進行干擾觀測，并計算干擾補償力矩，提高無模型控制算法的魯棒性。總控制力矩如下：

（13）

2.1 慢變子系統PD反饋控制算法

PD反饋控制是一種簡單有效的無模型控制方法，不需要獲取控制系統的數學模型，降低了控制器設計的難度，易于實現。慢變子系統采用PD算法進行機械臂軌跡跟蹤控制，如下式所示：

（14）

式中 和分別為期望轉角和角速度；和分別表示PD控制律的比例增益和差分增益。

2.2 快變子系統MFAC控制算法

2.2.1 離散非線性系統動態線性化

根據無模型自適應控制理論，對于離散時間非線性系統：

（15）

式中 和分別表示控制系統在k時刻的輸入向量和輸出向量；表示一個未知的動態非線性函數；，分別為系統使用的輸入、輸出向量的長度。滿足如下假設：

假設1：非線性函數對控制輸入的偏導數是連續可微的。

假設2：系統滿足廣義Lipschitz條件，即滿足以下條件：

（16）

當時，必存在一個時變參數矩陣，稱為偽雅可比矩陣，將系統轉換為以下緊格式動態線性化方法的泛模型：

（17）

其中，任意時刻是有界的且對角占優，即為中元素，其滿足：

（18）

式中 ，為的有界閾值參數，且滿足，其中。

原動態非線性系統的復雜行為特征，如非線性及時變參數等，被壓縮融入到時變的標量矩陣中，原系統的復雜且難以估計的動態特性可以轉變為一個被嚴格證明存在的偽雅可比矩陣。這種緊格式動態線性化方法的泛模型僅與閉環系統的I/O測量數據相關，不顯含結構模型參數，本質為數據驅動方法，因此可以適用于大多數時變非線性系統。另外可以被證明是動態有界的，通過設計適當的迭代估計算法可以保證泛模型的精度。

2.2.2 MFAC控制算法

將機械臂快變子系統的動力學方程離散化：

（19）

式中 為采樣時間間隔。則k時刻機械臂快變子系統的動力學方程可改寫為：

（20）

可見，快變子系統動力學方程符合MFAC控制所需的離散時間非線性系統形式。快變子系統控制力矩可表示為如下緊格式動態線性化模型：

（21）

其中：

。

定義MFAC輸入向量的準則函數如下：

（22）

式中 ，其中為機械臂期望振動響應，取；為權重因子，用于懲罰控制力矩發生突變。

將式（21）代入式（22），對求導，取極值，可得控制信號的迭代公式如下：

（23）

式中 為迭代步長，；為防止分母為0，。

在控制過程中，由于輸入控制轉矩向量和輸出運動向量的動態變化，獲得準確的值難以實現。可以通過系統輸入和輸出數據來估計。設計估計的準則函數：

（24）

式中 為的估計，為一個權重因子，用于懲罰估計中的較大變化。與式（23）的推導過程類似，的迭代過程如下：

（25）

式中 為迭代步長，；為小正值。

考慮到需滿足有界性要求，當矩陣元素超出閾值時，按如下規則進行初始化：

（26）

式中 ，為矩陣元素初值。

2.3 MESO設計

實際柔性機械臂系統運行時會受到外界擾動影響。設，對于柔性機械臂系統可改寫為：

（27）

式中 為總擾動。定義狀態量的觀測值為，其中，是對系統的廣義位移向量的估計，是對系統的廣義速度向量的估計，是對系統總擾動的估計。

設計ESO如下：

（28）

式中 為觀測誤差；為非線性函數向量，為非線性狀態觀測器的核心部分；，為非線性函數參數，在式（28）中有不同取值，分別取值和，分別取值和；為控制力增差矩陣；為觀測器濾波系數。通過仿真發現，對于低階系統，的選取按照菲波那契數列可以獲得較好的觀測效果［19］，參數選取如下：

（29）

非線性函數向量可以表示為：

（30）

式中 元素為特殊構造的非線性函數，遵循“小誤差，大增益；大誤差，小增益”的原則［15］，這種設計使其在處理系統模型不確定性和內外干擾時表現出色。傳統函數表達式為：

（31）

式中 決定函數的線性長度，，越大，線性區間越長；決定函數的線性區間長度。

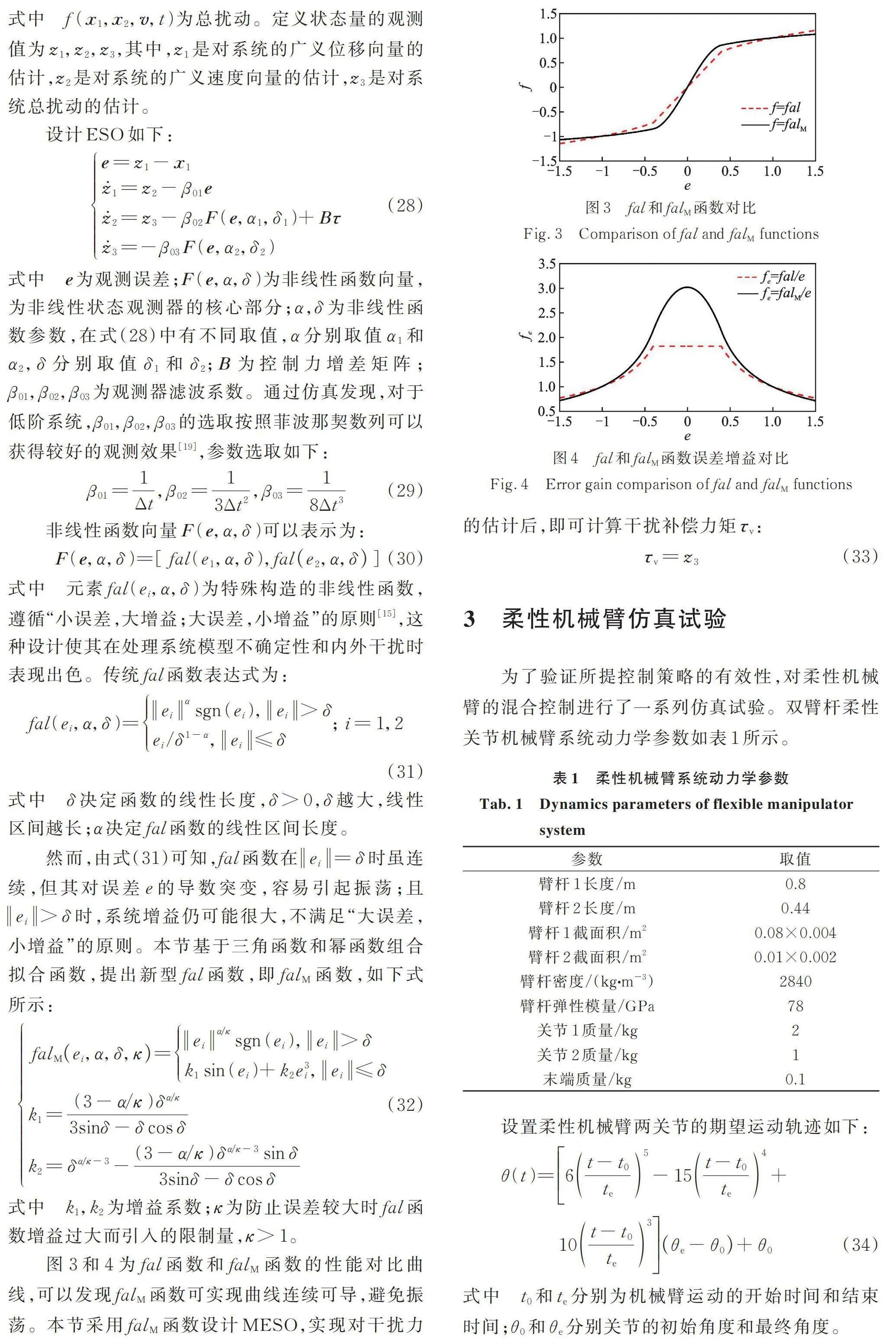
然而，由式（31）可知，函數在時雖連續，但其對誤差e的導數突變，容易引起振蕩；且時，系統增益仍可能很大，不滿足“大誤差，小增益”的原則。本節基于三角函數和冪函數組合擬合函數，提出新型fal函數，即函數，如下式所示：

（32）

式中 為增益系數；為防止誤差較大時fal函數增益過大而引入的限制量，。

圖3和4為fal函數和函數的性能對比曲線，可以發現函數可實現曲線連續可導，避免振蕩。本節采用函數設計MESO，實現對干擾力的估計后，即可計算干擾補償力矩：

3 柔性機械臂仿真試驗

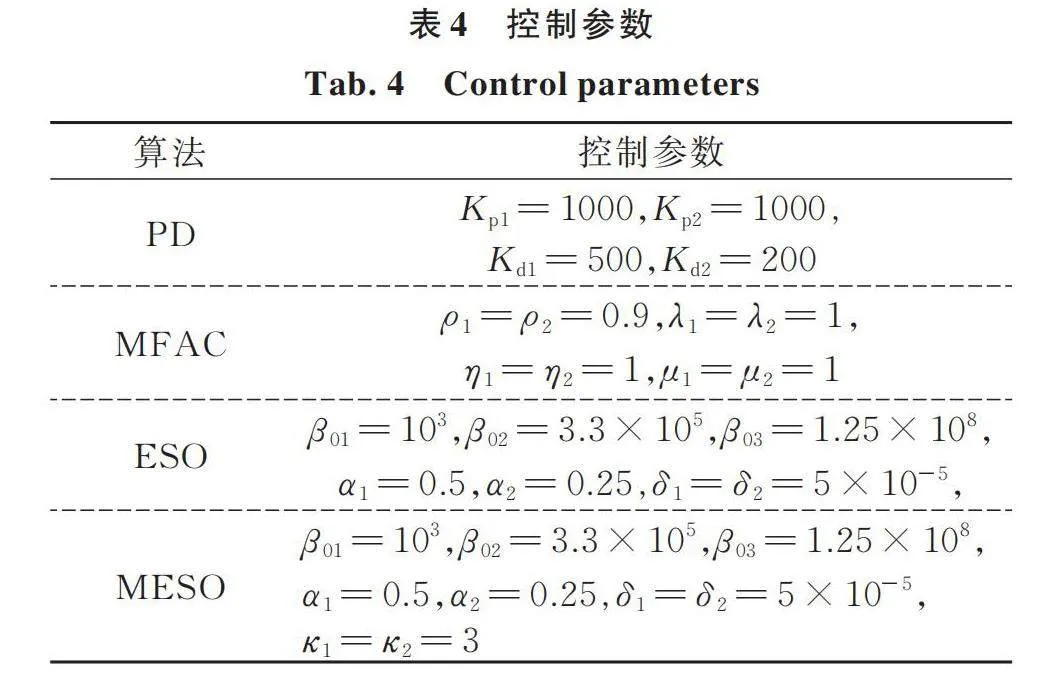
為了驗證所提控制策略的有效性，對柔性機械臂的混合控制進行了一系列仿真試驗。雙臂桿柔性關節機械臂系統動力學參數如表1所示。

設置柔性機械臂兩關節的期望運動軌跡如下：

（34）

式中 和分別為機械臂運動的開始時間和結束時間；和分別關節的初始角度和最終角度。

3.1 算例1：機械臂模型參數突變振動控制

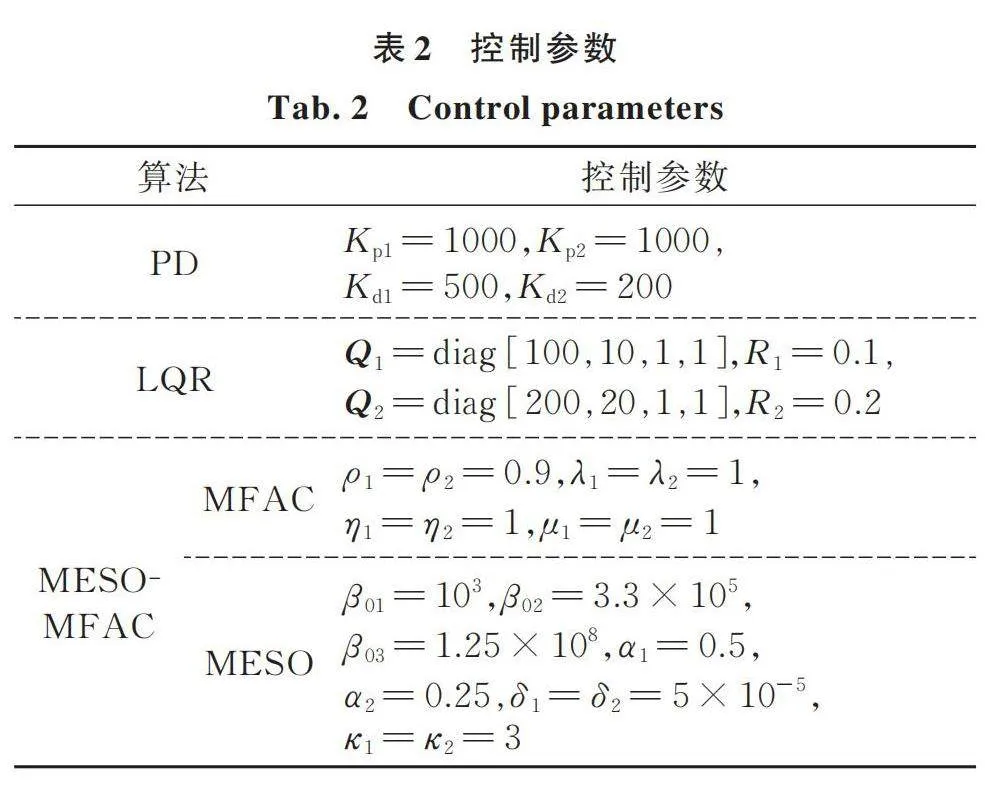
機械臂在執行抓取任務的過程中，包含被抓取物在內的機械臂系統參數會發生劇烈變化，這給基于模型的控制算法帶來了諸多不便。而本文提出的基于無模型的聯合控制方法在處理這類問題時具有很大優勢。在15 s時，機械臂抓取物體質量為1.5 kg。抓取后，機械臂系統質量參數發生突變。本節通過以下3組試驗來體現本文所提出的混合控制器的控制效果：（1）僅有基于PD控制的關節軌跡跟蹤，無振動控制算法；（2）基于PD控制的關節軌跡跟蹤控制和LQR振動控制的混合控制算法（PD+LQR）；（3）基于MESO干擾觀測器的PD控制和MFAC振動控制混合控制（PD+MESO?MFAC）。3種算法具有相同PD控制參數。LQR控制算法選取原則：控制輸入加權矩陣的值適當取小，狀態加權矩陣Q適當取大，在保證響應速度的同時可以避免響應波動過大［20］。MFAC控制參數參考文獻［13］選取；MESO參數按照式（31）以及參考文獻［19］選取。在滿足上述依據的前提下，對3種控制算法參數進行了調試，以確保控制效果最優。控制參數設置如表2所示。

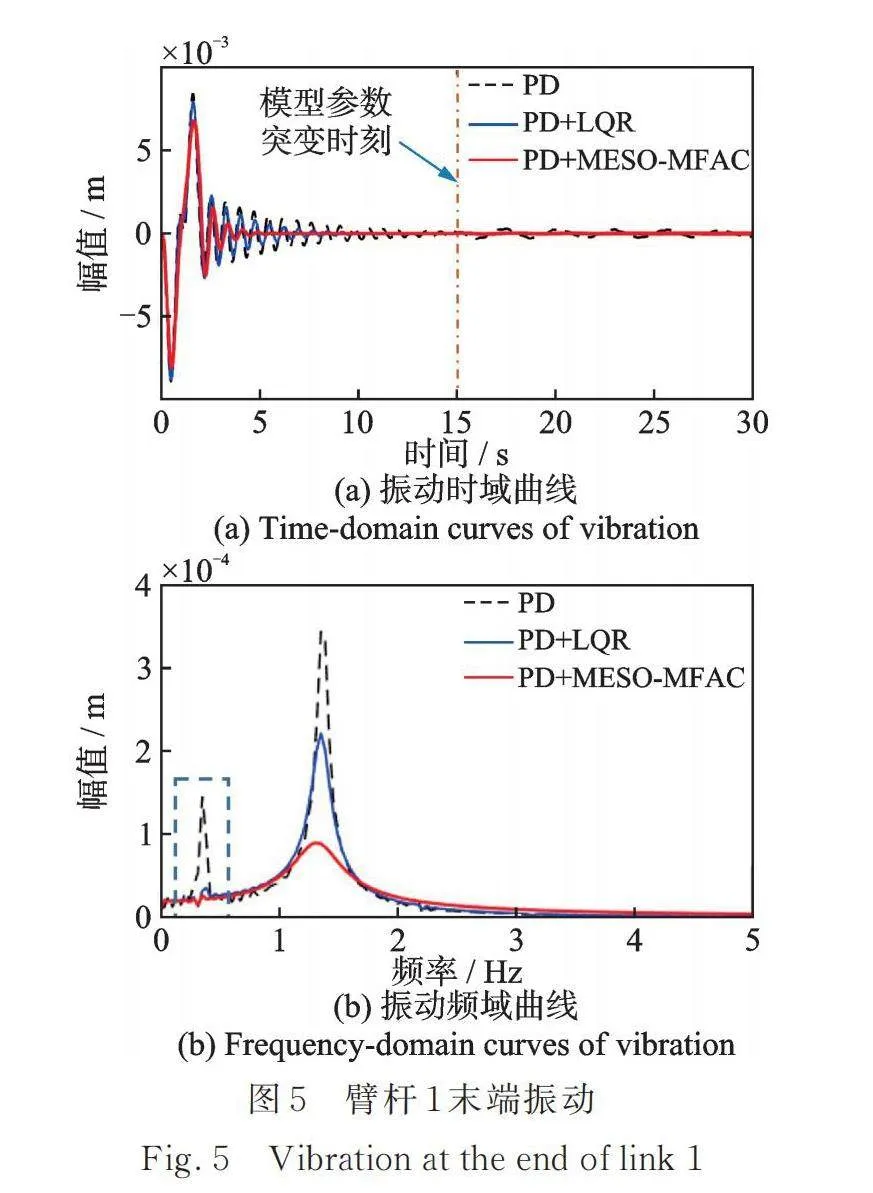
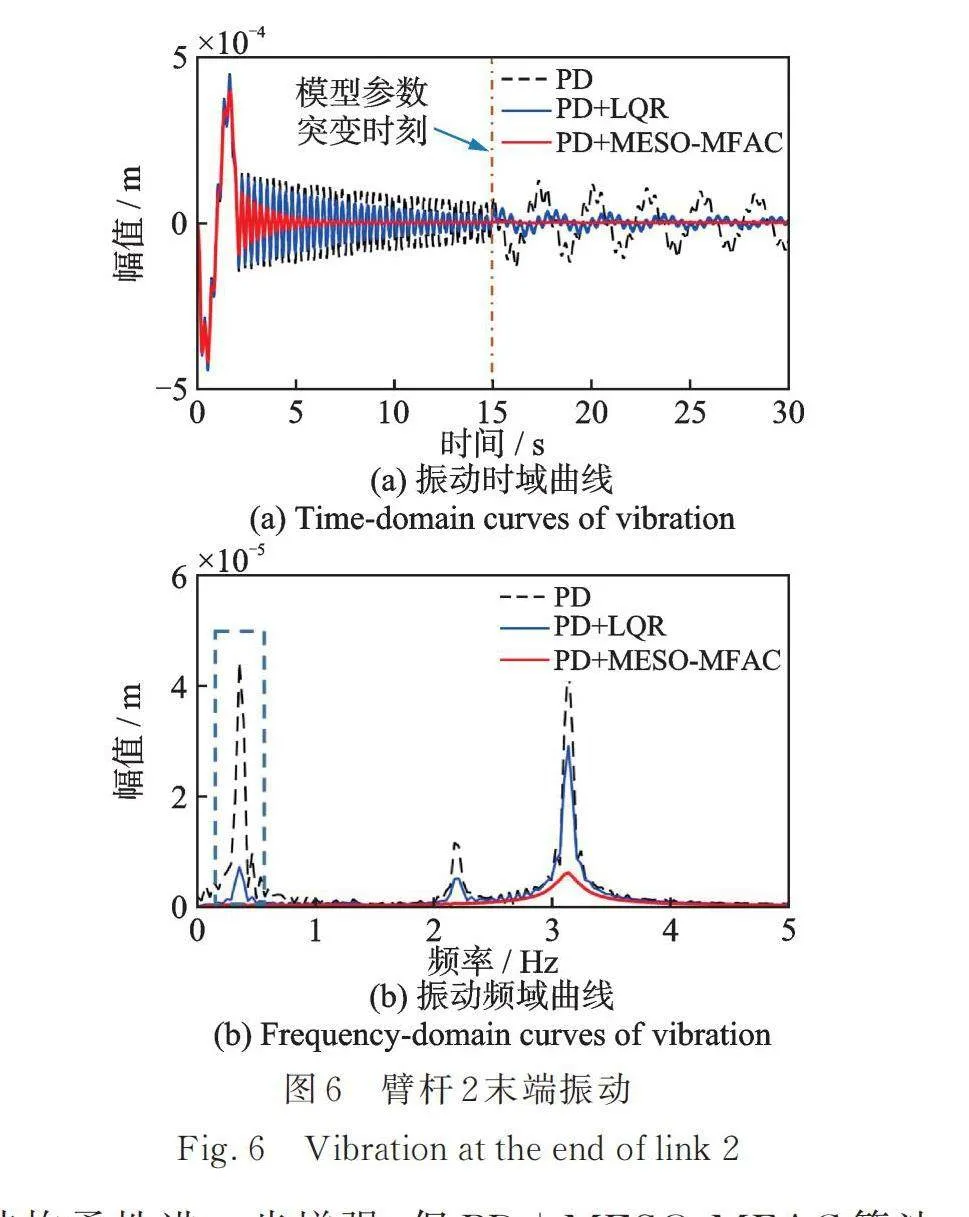
圖5和6為柔性機械臂桿末端振動響應結果。由圖可知，PD+LQR算法和PD+MESO?MFAC算法都在不同程度上實現了振動的有效抑制。然而，當系統在15 s發生模型參數突變后，由于基于模型的PD+LQR算法無法實時跟蹤系統參數，導致其振動抑制效果大打折扣。而PD+MESO?MFAC算法對參數突變具有很強的適應性，在參數突變發生后可以穩定保持其振動抑制效果。圖5（b），6（b）為振動頻率分析結果，可以看出，參數突變前臂桿1（1.3 Hz）、臂桿2（3.2 Hz）的振動都得到了有效的抑制。慣性參數突變后，臂桿1和2的固有頻率分別降低為0.36 Hz和0.39 Hz（見圖5（b）和6（b）虛線框），結構柔性進一步增強，但PD+MESO?MFAC算法的抑振效果基本不受干擾影響，表現出很強的魯棒性。

3.2 算例2：機械臂干擾力突變振動控制

機械臂在任務過程中受到干擾力的作用，會導致系統振動增強。本節通過以下4組試驗驗證本文設計算法在不同干擾力作用下的振動控制效果：（1）僅有基于PD控制的關節軌跡跟蹤，無振動控制算法；（2）基于PD控制的關節軌跡跟蹤控制和MFAC振動控制的混合控制算法（PD+MFAC）；（3）基于ESO干擾觀測器的PD控制和MFAC振動控制混合控制（PD+ESO?MFAC）。（4）基于MESO干擾觀測器的PD控制和MFAC振動控制混合控制（PD+MESO?MFAC）。

為驗證所提出算法的抗擾動性，設置柔性機械臂在不同類型和不同幅值干擾作用下（見表3）的干擾觀測和振動抑制效果。

4種算法具有相同PD控制參數，MFAC控制參數和ESO參數選取原則與3.1節一致，控制參數設置如表4所示。

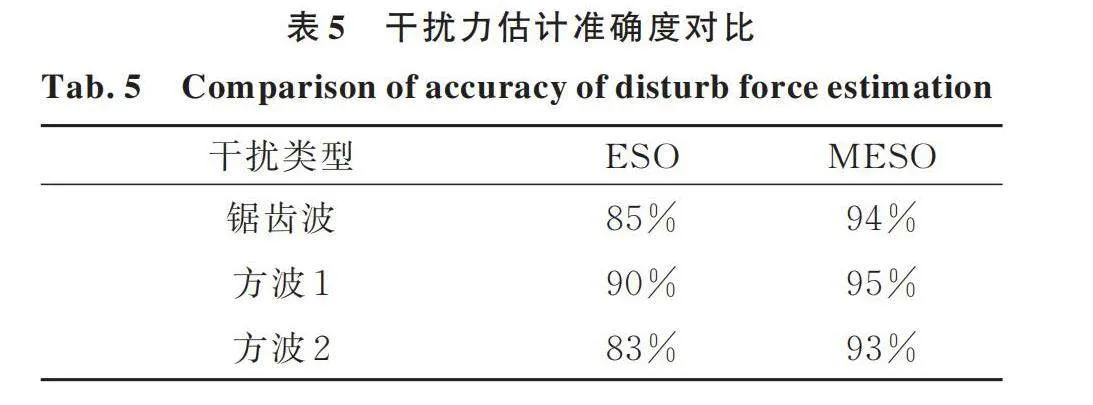
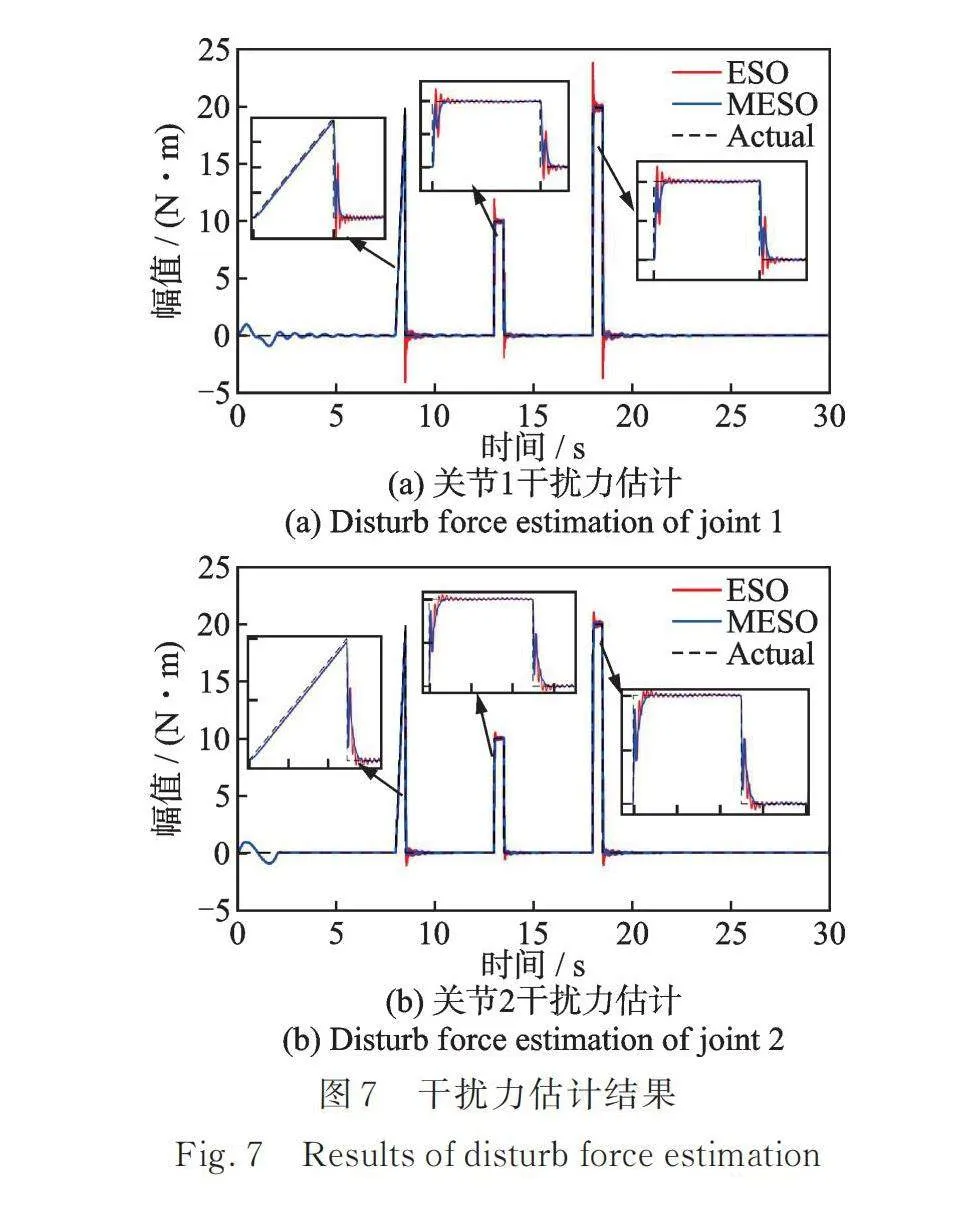
如圖7所示，無論關節1還是關節2，ESO和MESO算法均能有效估計外部干擾。ESO算法在干擾力突變時刻具有較大的估計超調量，尤其對于大幅值干擾力更為明顯。相對而言，MESO快速收斂且無超調，表現出更好的估計穩定性。由表5可知，在不同類型干擾突變時刻，MESO干擾估計準確率具有明顯優勢，平均辨識精度達到94%。并且隨著控制系統趨于穩定，干擾估計的準確率進一步提升。

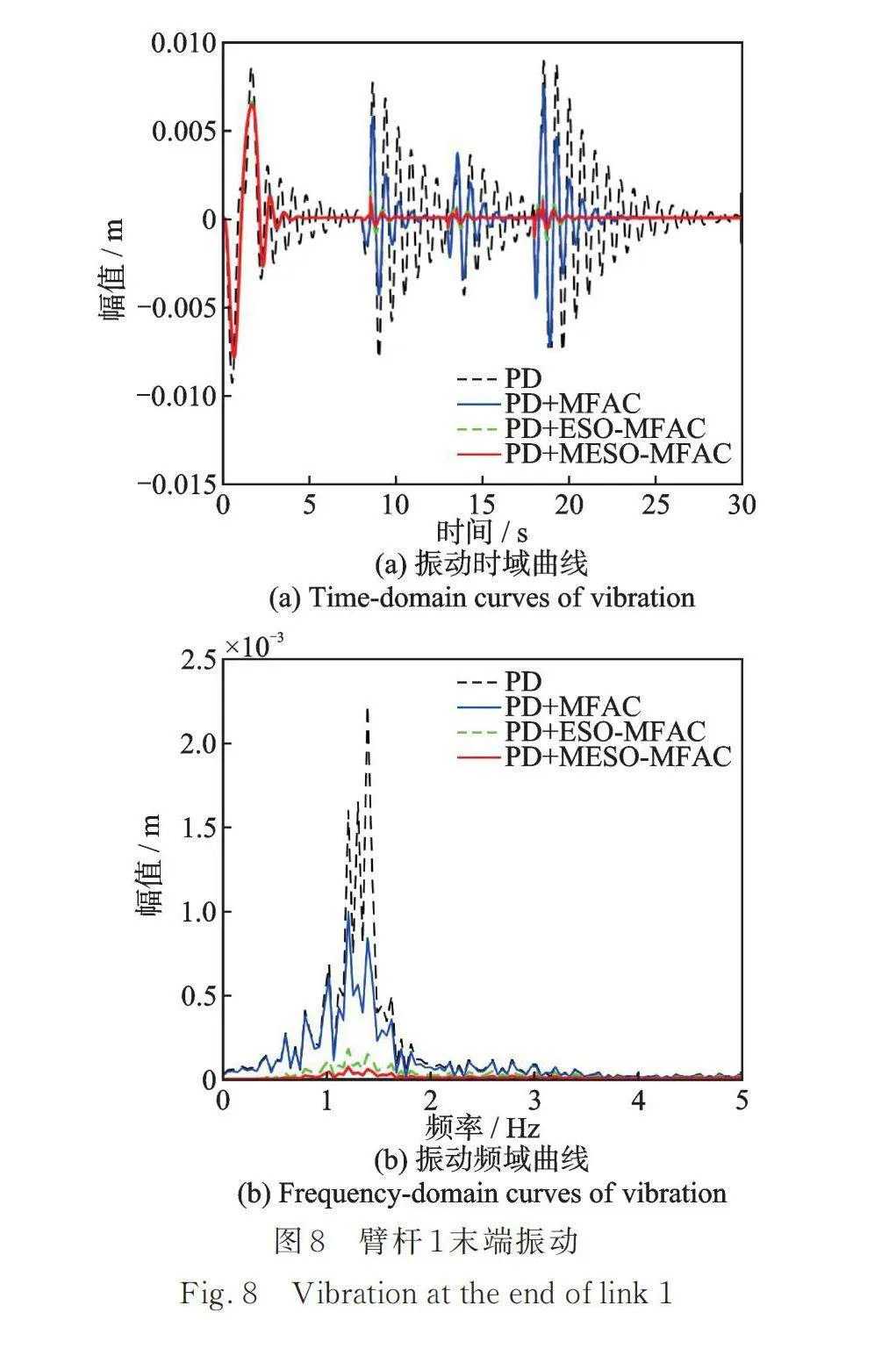
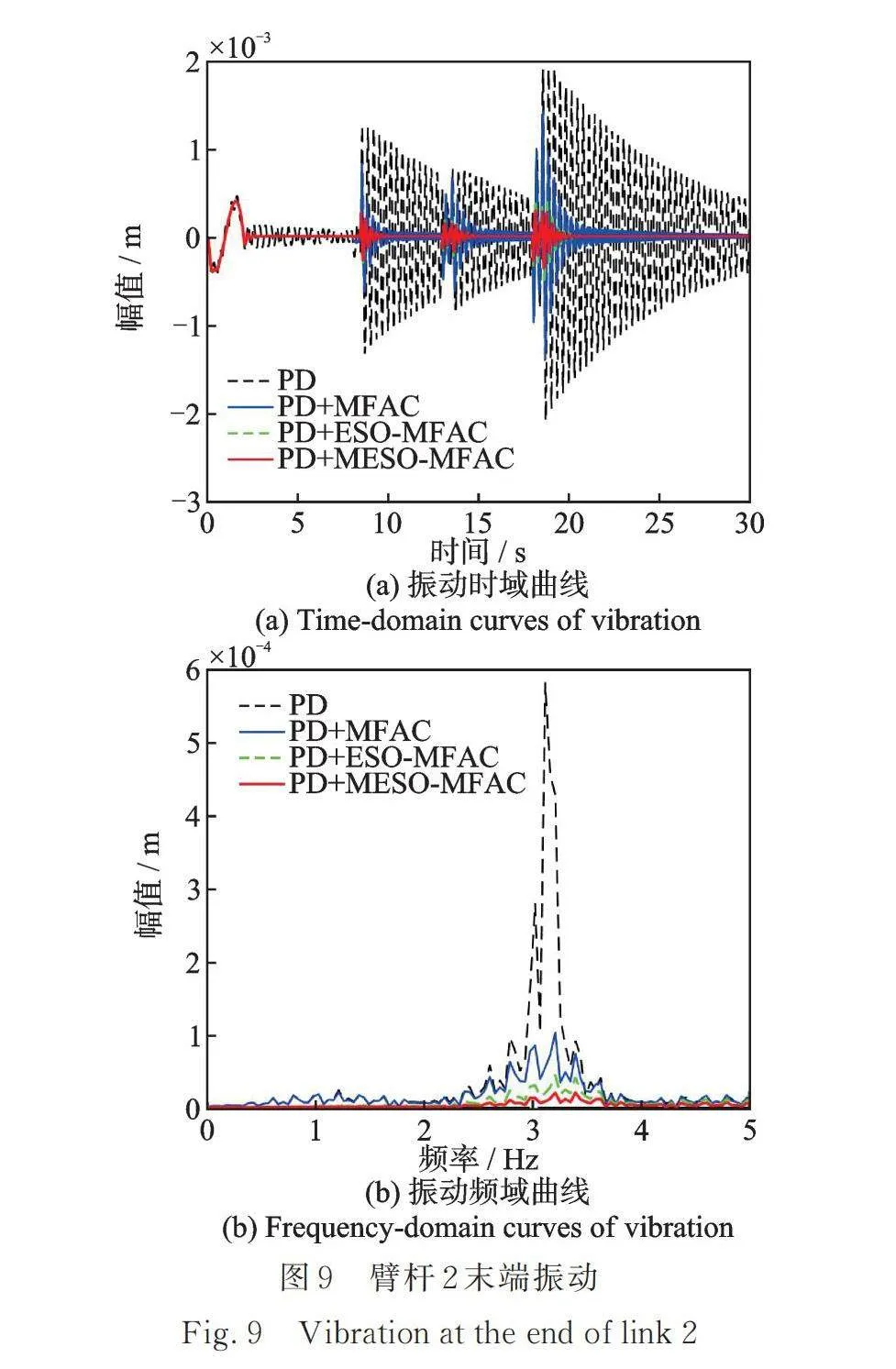
圖8和9為柔性機械臂桿末端振動響應結果。由圖可知，僅僅依賴于軌跡跟蹤的PD控制，柔性臂桿的振動抑制速度很慢。尤其是在受到外部干擾時，臂桿振動會進一步被激發。采用PD+MFAC算法進行振動抑制后，柔性臂桿振動可以被有效地抑制，但受突變干擾力影響明顯。采用PD+ESO?MFAC算法時，即使系統受到不同類型的突變干擾，振動依然得到了有效抑制，說明ESO對外部干擾進行有效估計并進行力矩補償后，干擾對控制系統的影響被削弱。由于本文提出MESO算法對不同干擾力具有更加有效的估計能力，PD+MESO?MFAC算法表現出更強的魯棒性。由圖8（b），9（b）振動的頻率分析結果可以看出，本文提出的PD+MESO?MFAC算法相較于PD+MFAC算法和PD+ESO?MFAC算法，減振效果大大提高（見表6）。

4 結 論

考慮到柔性機械臂精確，模型參數獲取不易，且在控制過程中容易受到外界干擾力。本文提出了一種基于MESO的無模型混合控制方法，用于柔性機械臂軌跡跟蹤和振動控制。所提方法的優勢體現在以下方面：

（1）與基于精確模型參數的控制方法相比，所提方法對模型參數的精度要求不高。

（2）通過構造新型fal函數，提出MESO算法，對未知動態干擾進行更加有效估計，干擾力估計準確率達94%以上。

（3）與傳統MFAC算法相比，所提算法對未知突變干擾下的柔性機械臂具有良好的振動控制效果，系統魯棒性強。

綜上所述，所提出的混合控制策略不僅保證了柔性機械臂較高的軌跡跟蹤精度，而且快速降低了柔性臂桿的振動，顯著提高了柔性機械臂的工作效率。

參考文獻：

［1］尚東陽，李小彭，尹猛，等. 采用干擾補償模糊整定的雙柔性機械臂抑振策略［J］. 振動工程學報，2024，37（1）： 1-10.

SHANG Dongyang，LI Xiaopeng，YIN Meng，et al. Vibration suppression strategy for dual-flexible manipulator using disturbance compensation fuzzy setting control method［J］. Journal of Vibration Engineering，2024，37（1）： 1-10.

［2］Nguyen V B，Bui X C. Hybrid vibration control algorithm of a flexible manipulator system［J］. Robotics，2023，12（3）： 73.

［3］Song N N，Zhang M R，Li F，et al. Dynamic research on winding and capturing of tensegrity flexible manipulator［J］. Mechanism and Machine Theory，2024，193： 105554.

［4］Shen H，Fan J H. Dynamic modeling and simulation of a folding-link flexible manipulator based on the bezier interpolation method［J］. Journal of Vibration Engineering & Technologies，2024，12（2）： 1525-1535.

［5］Shi M M，Rong B，Liang J，et al. Dynamics analysis and vibration suppression of a spatial rigid-flexible link manipulator based on transfer matrix method of multibody system［J］. Nonlinear Dynamics，2023，111（2）： 1139-1159.

［6］Thakur S，Barai R K. Sliding mode control of a two-link flexible manipulator for reduced vibration in the presence of unmatched uncertainty and time-varying external disturbance［J］. International Journal of Automation and Control，2024，18（2）： 161-183.

［7］Sarkhel P，Dikshit M K，Pathak V K，et al. Robust deflection control and analysis of a fishing rod-type flexible robotic manipulator for collaborative robotics［J］. Robotics and Autonomous Systems，2023，159： 104293.

［8］Zhang S，Wu Y，He X Y. Neural network-based cooperative trajectory tracking control for a mobile dual flexible manipulator［J］. IEEE Transactions on Neural Networks and Learning Systems，2023，34（9）： 6545-6556.

［9］Liu S Y，Yang H L，Liu Z J. Adaptive neural network independent joint-based control for an ODE-PDE rigid-flexible manipulator with multiple constraints［J］. Journal of Vibration and Control，2024，30（7-8）： 1647-1658.

［10］Xie L M，Yu X Y，Chen L. Robust fuzzy sliding mode control and vibration suppression of free-floating flexible-link and flexible-joints space manipulator with external interference and uncertain parameter［J］. Robotica，2022，40（4）： 997-1019.

［11］Feng C L，Chen W D，Shao M Q，et al. Trajectory tracking and adaptive fuzzy vibration control of multilink space manipulators with experimental validation［J］. Actuators，2023，12（4）： 138.

［12］Mei Y F，Liu Y. ILC-RBNNF-based vibration control of a rotatable manipulator with time-varying output constraints［J］. IE3ba2fd121d14fad8cfb6643e22e94317EE Transactions on Systems Man Cybernetics Systems，2023，53（10）： 6416-6425.

［13］侯忠生. 無模型自適應控制的現狀與展望［J］. 控制理論與應用，2006，23（4）： 586-592.

HOU Zhongsheng. On model-free adaptive control： the state of the art and perspective［J］. Control Theory & Applications，2006，23（4）： 586-592.

［14］浦玉學，陳演，李孝寶. 柔性關節空間機械臂傳感容錯無模型自適應控制［J］. 宇航學報，2024，45（1）： 133-141.

PU Yuxue，CHEN Yan，LI Xiaobao. Sensor fault-tolerant model-free adaptive control of flexible joint space manipulator［J］. Journal of Astronautics，2024，45（1）： 133-141.

［15］Liu X J，Zhang G M，Shi Z H. Improved current control for PMSM via an active disturbance rejection controller［J］. European Journal of Control，2024，78： 101005.

［16］Shang D Y，Li X P，Yin M，et al. Vibration suppression method for dual-flexible manipulator considering bearing friction based on nonlinear disturbance observer［J］. Journal of Mechanical Science and Technology，2024，38（2）： 885-900.

［17］李城. 雙連桿柔性機械臂智能自適應振動控制研究［D］. 廣州： 華南理工大學，2018.

Li Cheng. Research on intelligent adaptive vibration control of two-link flexible manipulator［D］. Guangzhou： South China University of Technology，2018.

［18］Li B，Li X Y，Gao H J，et al. Advances in flexible robotic manipulator systems-part I： overview and dynamics modeling methods［J］. IEEE/ASME Transactions on Mechatronics，2024，29（2）： 1100-1110.

［19］韓京清. 自抗擾控制技術： 估計補償不確定因素的控制技術［M］. 北京： 國防工業出版社，2008.

HAN Jingqing. Active Disturbance Rejection Control Technique： the Technique for Estimating and Compensating the Uncertainties［M］. Beijing： National Defense Industry Press，2008.

［20］Li J，Zhang L Y，Zhang M H，et al. Multi-modal vibration control for all-clamped plate subjected to periodic disturbances by ESO-based frequency-shaped LQR［J］. Mechanical Systems and Signal Processing，2023，201： 110658.

Disturb force observation and model-free vibration control of flexible manipulator

Pu Yu-xue1，2，Gu Yan1，ZHANG Chong-feng3，Zou Huai-wu3

（1.College of Civil Engineering，Hefei University of Technology，Hefei 230009，China； 2.Anhui Key Laboratory of Civil Engineering Structures and Materials，Hefei 230009，China； 3.National Key Laboratory of Aerospace Mechanism，Shanghai 201108，China）

Abstract： In order to suppress the nonlinear vibration during the motion of a flexible manipulator，a model-free hybrid control strategy of trajectory tracking and vibration suppression based on a novel online observation of disturb forces is proposed. The Lagrange equation and singular perturbation method are employed to model and decouple the dynamics of the manipulator，which are decomposed into a slow subsystem representing rigid motion and a fast subsystem representing flexible vibration. Considering the complexity of modeling and uncertainty of model parameters，PD control method is adopted to realize trajectory tracking，and model-free adaptive control algorithm is proposed to realize nonlinear vibration control of flexible links. To solve the control divergence problem caused by unknown external disturb forces，a modified extended state observer is proposed to online estimate and real-time compensate the disturb force，which can improve the convergence performance of model-free vibration control algorithm effectively. The simulation results show that the proposed method can effectively suppress the vibration of the flexible manipulator in the presence of disturb force，and has good dynamic performance and robustness.

Key words： flexible manipulator；vibration control；model free adaptive control；disturb observer

作者簡介： 浦玉學（1987―），男，博士，副教授。E-mail： puyuxue@hfut.edu.cn。

通訊作者： 張崇峰（1968―），男，博士，教授。E-mail： robot_zcf@126.com。