面向動態特性指標的機電伺服系統PID設計方法

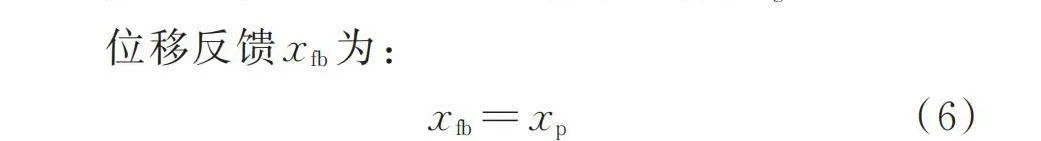
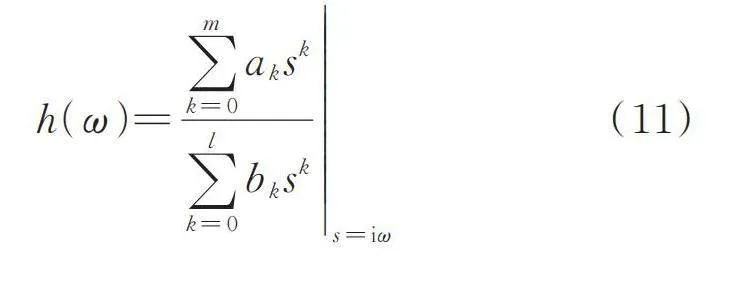
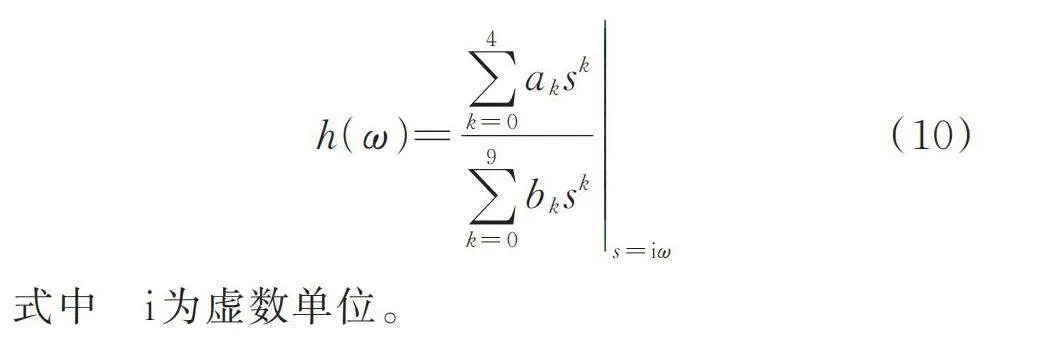
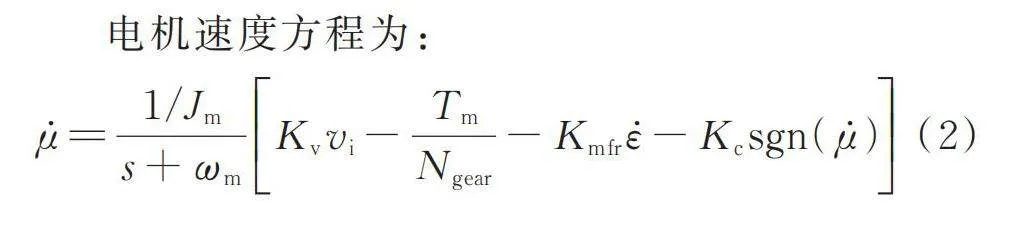
摘要： 針對機電伺服系統PID參數設計難以充分考慮動態特性（幅?相頻特性）指標的問題，提出了面向動態特性指標的PID設計方法。基于動力學方程建立了機電伺服系統的9階傳遞函數（Transfer Function，TF）模型。運用勞斯判據和TF系數之間的關系補充了系統的穩定性約束和TF系數的相容性約束，以保證PID設計過程中系統的穩定性和TF系數的相容性。在此基礎上，基于參數辨識的思想，利用改進的有理分式多項式法辨識TF模型中各個參數，從而快速確定了滿足動態特性指標的PID參數，提高了設計效率，并且通過調整指標數據辨識得到多組滿足原指標的控制器參數。仿真結果表明：設計得到的PID參數不僅滿足動態特性指標要求，而且兼顧了系統穩定性和TF系數的相容性，設計結果與仿真吻合良好。

關鍵詞： PID控制； 參數辨識； 動態特性指標； 機電伺服系統

中圖分類號： TP273； TM341 文獻標志碼： A 文章編號： 1004-4523（2024）10-1767-08

DOI：10.16385/j.cnki.issn.1004-4523.2024.10.015

引 言

伺服系統是飛行器控制系統的重要組成部分，通過接收來自控制系統的指令，控制空氣舵偏轉或噴管擺動來產生控制力，實現飛行器的姿態控制和軌跡控制［1］。隨著功率電子技術的發展，以機電作動器（Electromechanical Actuator，EMA）為位移輸出的機電伺服系統逐漸取代了液壓伺服系統。由于取消了傳統液壓作動器內部的液壓系統，EMA具有精度高、維護成本低、重量輕、環境適應性強等優點，近年來在航空航天領域得到廣泛使用［2?5］。

機電伺服系統的控制算法一般包括PID控制［6］、神經網絡控制［7?8］、自抗擾控制［9?10］、魯棒控制［11］和滑模控制［12］等，其中常規PID控制由于結構簡單、實時性好、魯棒性較強等特點，在控制領域得到了廣泛應用。但是PID控制的性能依賴于參數整定，目前，PID參數整定的方法主要分為以下幾類：Ziegler?Nichols法、ISTE最優設定法、經驗法、辨識法、開環階躍響應曲線法、閉環測試法等［13］，上述方法大多是針對單閉環PID控制器進行設計的，且很大程度上和設計者的工程經驗有關。針對該問題，李璀璀等［14］提出了基于遺傳算法的模糊PID控制方法，提高了PID參數全局尋優的能力，且仿真結果表明，相較于模糊PID控制，該方法能明顯改善電動舵機的動穩態性能；陳家俊等［15］以伺服系統為研究對象提出了一種基于機器學習和模糊控制的PID參數整定方法，該方法經過學習后能自動給出幾組較優控制參數，避免了手動整定PID參數，節省了時間和人力成本；Pradhan等［16］提出了一種PID非線性自整定方法，該方法能在線辨識并實時更新模糊控制系統的參數，實現了對柔性機械手的高精度跟蹤；邱亮［17］基于階躍響應的模型辨識方法提出了一種PID控制器定量自整定方法，并開發了相應PID自整定軟件，提高了控制器的自動化程度和控制精度；Davanipour等［18］采用混沌優化方法提出了一種基于模糊小波神經網絡模型的自整定PID控制器，實驗表明自整定得到的PID參數有較好的控制性能，系統響應的穩態誤差小，跟蹤性較好。以上研究工作對PID的設計提供了思路。然而，上述方法的設計目標大多基于控制精度，面向動態特性指標的PID設計研究還鮮有報道。

伺服系統的動態特性對姿態控制系統設計有重要影響，因此，姿控專業對其提出了嚴格的指標要求，包括幅頻特性和相頻特性兩方面。工程中，不同飛行器的空氣舵或擺動噴管轉動慣量不同，當選用現成的伺服系統進行飛行器姿態控制時，往往需要考慮在不改變伺服系統硬件的情況下，通過調整PID控制參數使其滿足指標要求。針對以上問題，本文以采用PID控制的機電伺服系統為研究對象，建立了系統的9階傳遞函數（Transfer Function，TF）模型，在約束條件下利用動態特性指標數據設計出了滿足指標要求的PID參數MMoE6yxAfOYDONF/rIj/qg==，用建立的SIMULINK非線性仿真模型驗證了該方法的正確性。

1 機電伺服系統建模

1.1 系統組成

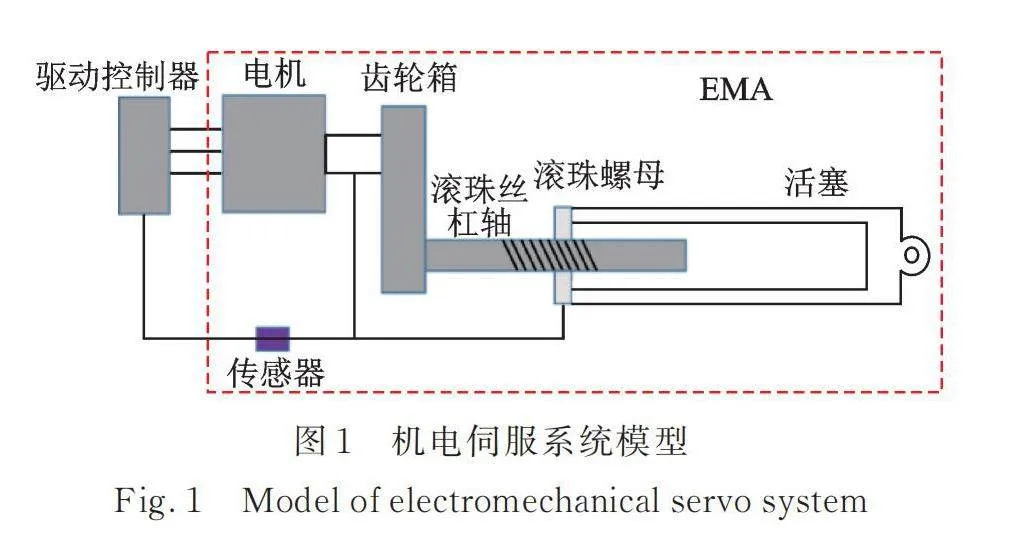
機電伺服系統由驅動控制器和EMA組成，如圖1所示，其工作原理為：驅動控制器接收來自控制系統的位置指令和電源輸入，驅動電機輸出轉速和扭矩，然后通過齒輪機構和滾珠絲杠軸帶動滾珠螺母輸出直線位移，最后傳感器反饋位移形成閉環控制。由于電壓和功率有限，因此驅動控制器存在電氣飽和的非線性因素。

1.2 系統非線性動力學

機電伺服系統是一個有電流環、速度環、位置環的三環控制系統［19］，為滿足伺服系統快速、精確控制的需求，一方面通過選擇合適的元器件使傳感器、控制器和執行機構之間的延遲盡量小，另一方面要求電流環調節器具有較高的帶寬和較小的時間常數，同時在EMA電機和控制器選型時一般要求其電氣時間常數遠小于機械時間常數，因此，在總體集成建立動力學模型時可以忽略伺服電機電流環控制的動態［2］。故本文驅動控制器采用位移反饋、電機速度反饋和PID控制實現對控制系統位置指令的閉環跟蹤，動力學建模如下［20］：

控制器輸出電壓為：

（1）

式中 分別為PID控制器的比例增益、積分增益和微分增益；為電機速度反饋增益；為電機轉角；為電機速度；為控制系統輸入的位置指令；為位移反饋。

電機速度方程為：

（2）

其中，電機向滾珠絲杠輸出的扭矩為：

（3）

式中 為電機轉動慣量；為Laplace域復變量；為電機帶寬；為電機轉矩增益；為相對角位移（電機負載）；為滾珠絲杠齒輪轉角；為減速比（電機轉角與滾珠絲杠轉角比）；為齒輪副剛度；為電機齒輪摩擦系數；為電機庫倫摩擦力矩幅值。

作動軸的位置為：

（4）

式中 為絲杠及其齒輪的轉動慣量；為齒輪副的機械效率；為滾珠絲杠傳動比（絲杠轉動1 rad對應的活塞伸長量）；為滾珠絲杠阻尼系數；為活塞軸受到的力；為艙壁、作動器和負載串聯的總剛度；為活塞軸到負載旋轉軸的力臂；為負載轉角；為活塞伸長量；為活塞軸端部實際位移。

負載繞轉軸轉動，運動方程為：

（5）

式中 為負載繞轉軸的轉動慣量，通過減速比關系折算到電機輸出軸上；為黏性阻尼系數；為外界輸入力矩；為負載繞轉軸的轉動剛度，對于空氣舵和球窩擺動噴管這類操縱機構，=0。

位移反饋為：

（6）

由于EMA性能受負載、非線性等因素影響較大，考慮到工程實際，為優化伺服系統的性能，改善系統穩定性、降低噪聲干擾和保護關鍵組件，通常在控制器中加入一個低通濾波器，其傳遞函數為：

（7）

式中 為濾波器參數。

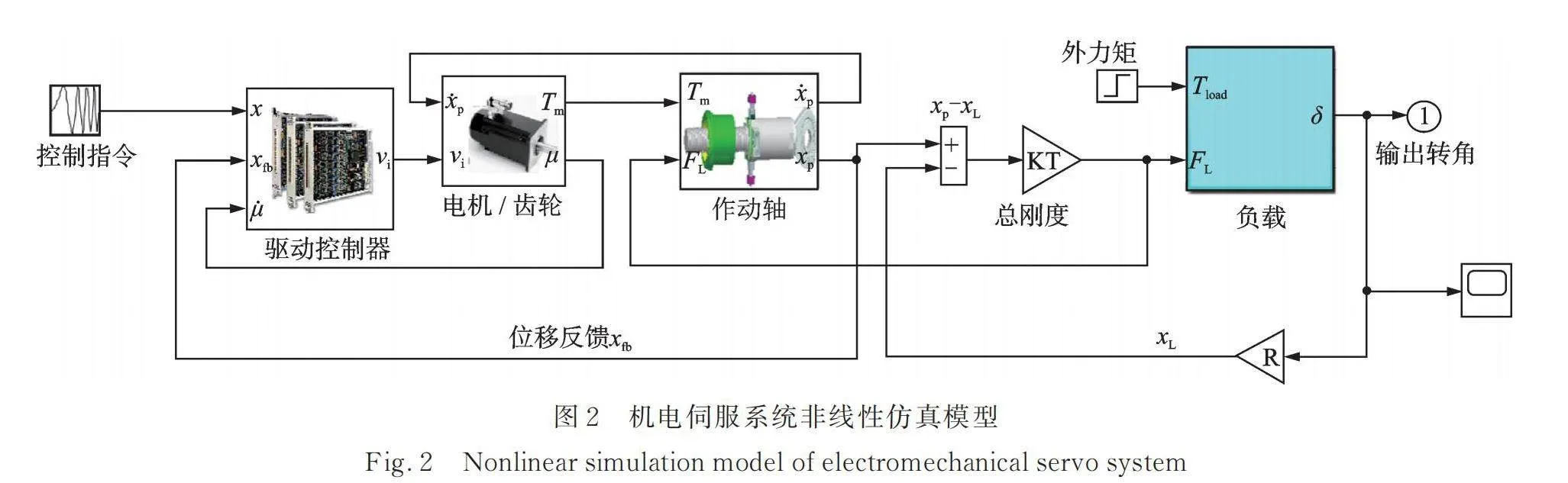
綜上所述，機電伺服系統是一個復雜的非線性系統，綜合式（1）～（7）可建立如圖2所示的非線性仿真模型，用于后續仿真檢驗。

1.3 系統傳遞函數

伺服系統的動態特性一般采用簡諧或掃頻激勵測試獲得。工程中空載測試時，外界輸入力矩，負載可采用一個剛體慣量盤。不計式（7）濾波器和摩擦的影響，對式（1）～（5）進行Laplace變換，得到整個系統的TF：

（8）

其中：

其中：

考慮濾波器時，系統的TF可由與相乘得到，此時TF的形式為：

（9）

其中，與的系數表達式均已給出，，的表達式可由與的系數相乘得到，這里不再一一給出。對于系統零次項系數，在不考慮濾波器時有，考慮濾波器時有，表示在靜態和低頻輸入指令時，系統響應與偏轉指令是1∶1傳遞，體現了位置跟蹤系統的特征。

2 面向動態特性指標的PID設計方法

對于式（9）中的傳遞函數，當系統參數確定時，各系數均只為的函數。通過動態特性指標設計可以轉換為參數辨識問題，即嘗試通過用式（9）的傳遞函數擬合動態指標數據得到滿足指標的，，進而由，確定PID控制參數。

實際的參數辨識一般不直接進行傳遞函數的測試，而是通過頻響測試完成傳遞函數參數的辨識。在本文PID參數設計的問題中，將動態特性的指標數據作為測試數據進行辨識。

式（9）對應的頻響函數為：

（10）

式中 i為虛數單位。

2.1 帶約束的有理分式正交多項式法

式（10）的參數辨識問題最終可以通過求解一組線性方程來得到最小二乘誤差意義上的解，但最大的困難在于方程組是病態的。對此，Richardson等［21］提出了有理分式正交多項式法，用復正交多項式重新表征頻響函數，可使數值病態問題得到有效改善。該方法是針對一般的線性系統提出的，不能直接處理約束條件，需要對其進行改進，在目標函數中補充約束方程。一般線性系統的頻響函數均可表示為如下式的有理分式：

（11）

式中 和為待辨識的參數。C2ED2+wa0jUqOfYWGXByvl+rgd9LV1kEM2iTUQqc9R4=

在每個測試頻點上將頻響函數改寫為用半函數表示的正交多項式：

（12）

式中 和為Forsythe多項式（半函數）的正交基，滿足正交條件：

（13）

（14）

式中 上標“*”表示共軛。當求解出頻響函數中的系數和時，即可通過轉換矩陣求解得到傳遞函數中的系數和：

（15）

式中 ；；；；，為轉換矩陣。同時，不失一般性，假設分母最高階系數。

此時用正交多項式表示的誤差向量為：

（16）

2.2 構造目標優化函數

參數辨識本質上是一個優化問題，因此可構造最小二乘擬合目標函數：

（17）

對于給定的系統，被控對象參數已知時，只為PID控制器3個參數的函數。

對于式（11）的頻響函數，含有個未知系數和3個自由度，即存在個系數之間的約束條件。

同時，為保證采用PID控制后伺服系統的穩定性，系統特征方程的系數需要滿足穩定判據。因此，運用勞斯判據可得到個穩定性約束，加上系數之間的約束總共有個關于，的約束。這些約束可通過轉換矩陣加到目標函數中，最終問題可轉換為求解約束條件下的多參數優化問題，數學上可表述為求使最小，即

（18）

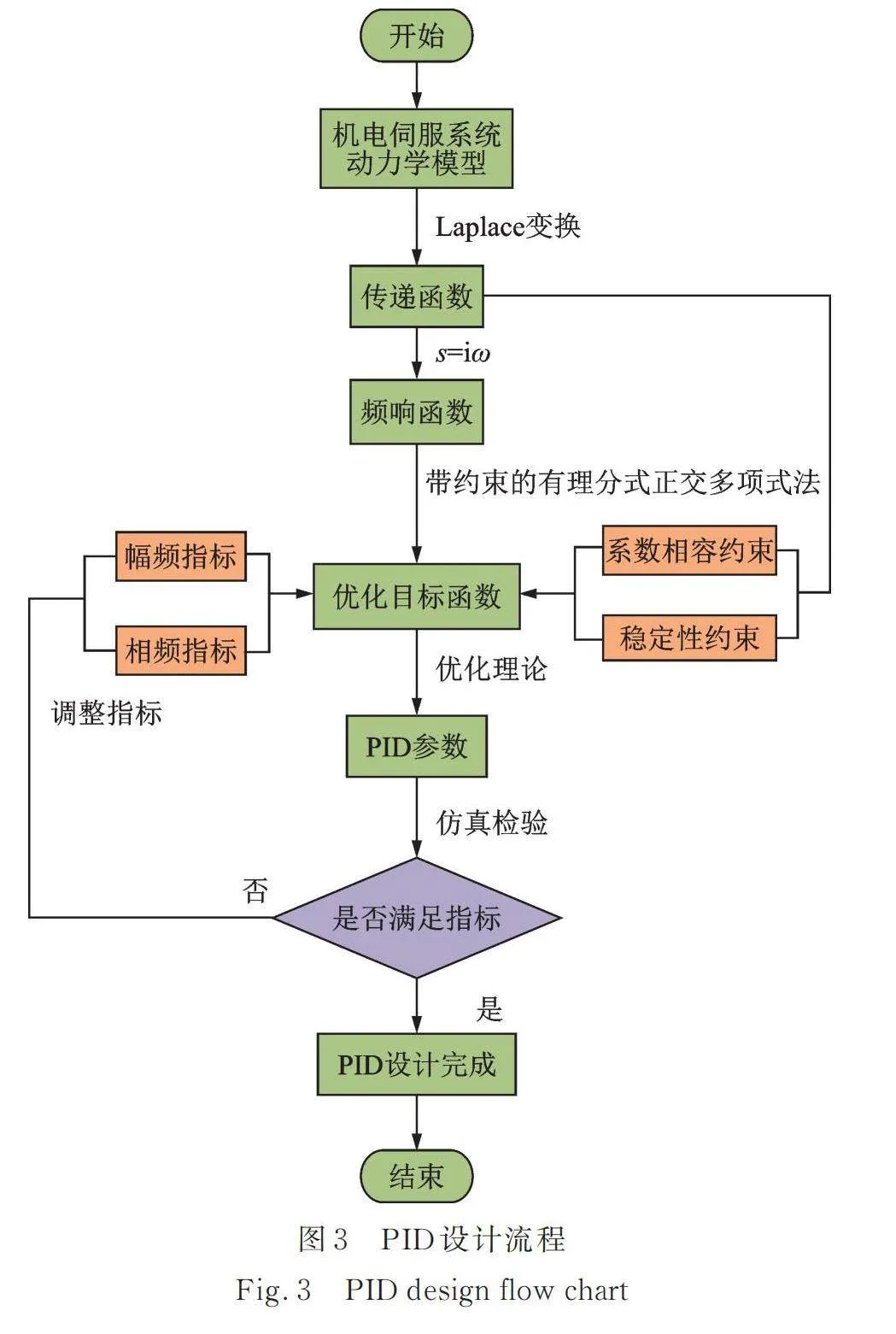
式中 為系數之間的等式約束，由于勞斯判據中包含系數的乘積，因此為待求系數的非線性不等式約束。對于式（18）的優化問題，可利用MATLAB非線性規劃求解器fmincon進行求解，fmincon通過使用拉格朗日乘子法能夠有效處理等式和不等式約束，并結合內點法、序列二次規劃法等方法來尋找最優解。求解得到正交多項式的系數向量和后，通過轉換矩陣變換即可得到傳遞函數的系數和，進而根據，與PID參數的關系求得，完整的PID設計流程如圖3所示。

3 數值仿真檢驗

3.1 數值仿真案例

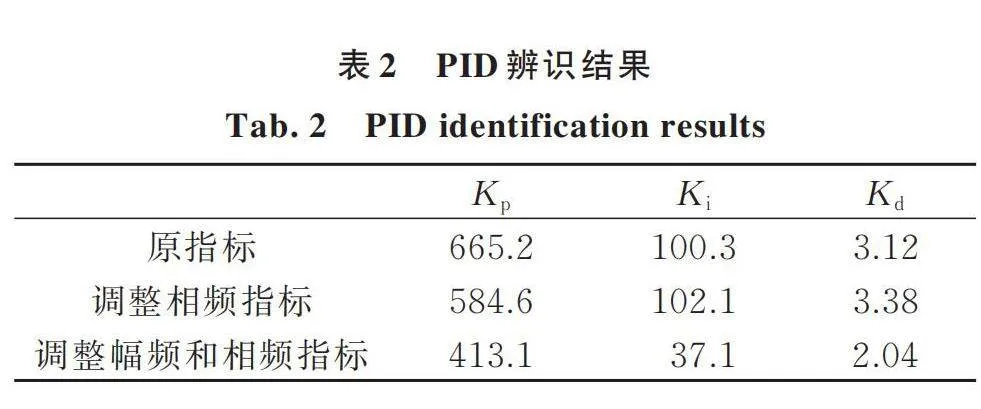
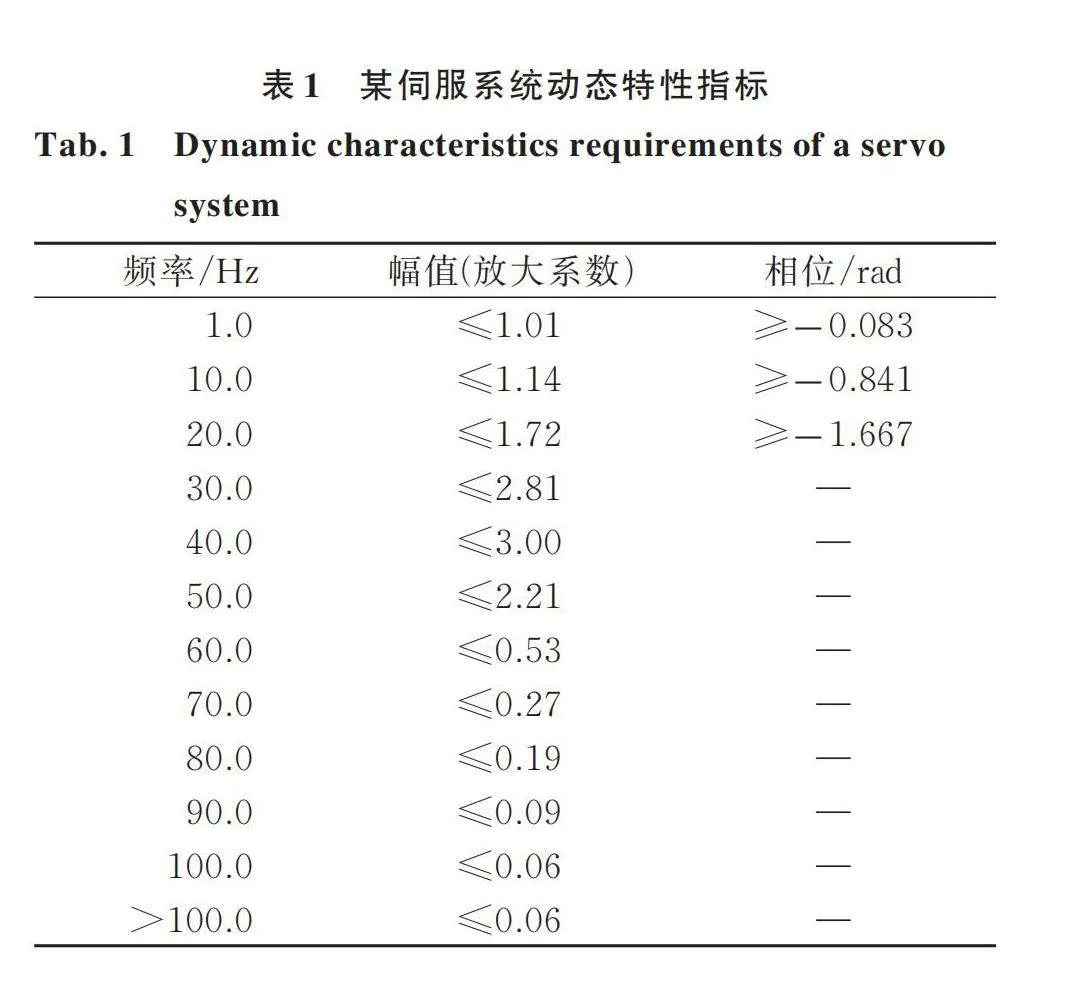
工程中伺服系統的動態特性指標往往是在特定的離散頻點上給出的，表1為某機電伺服系統的動態特性指標數據。當將指標數據作為測試數據進行PID設計時，可用插值的方法將所有頻點上的指標數據補全，當用線性插值補全所有指標數據時，辨識結果見表2。

3.2 結果分析與討論

將表2中辨識的PID參數代入非線性仿真模型進行檢驗，輸入伺服正弦掃頻指令，輸出伺服擺角，由二者可得到幅頻和相頻特性，結果如下：

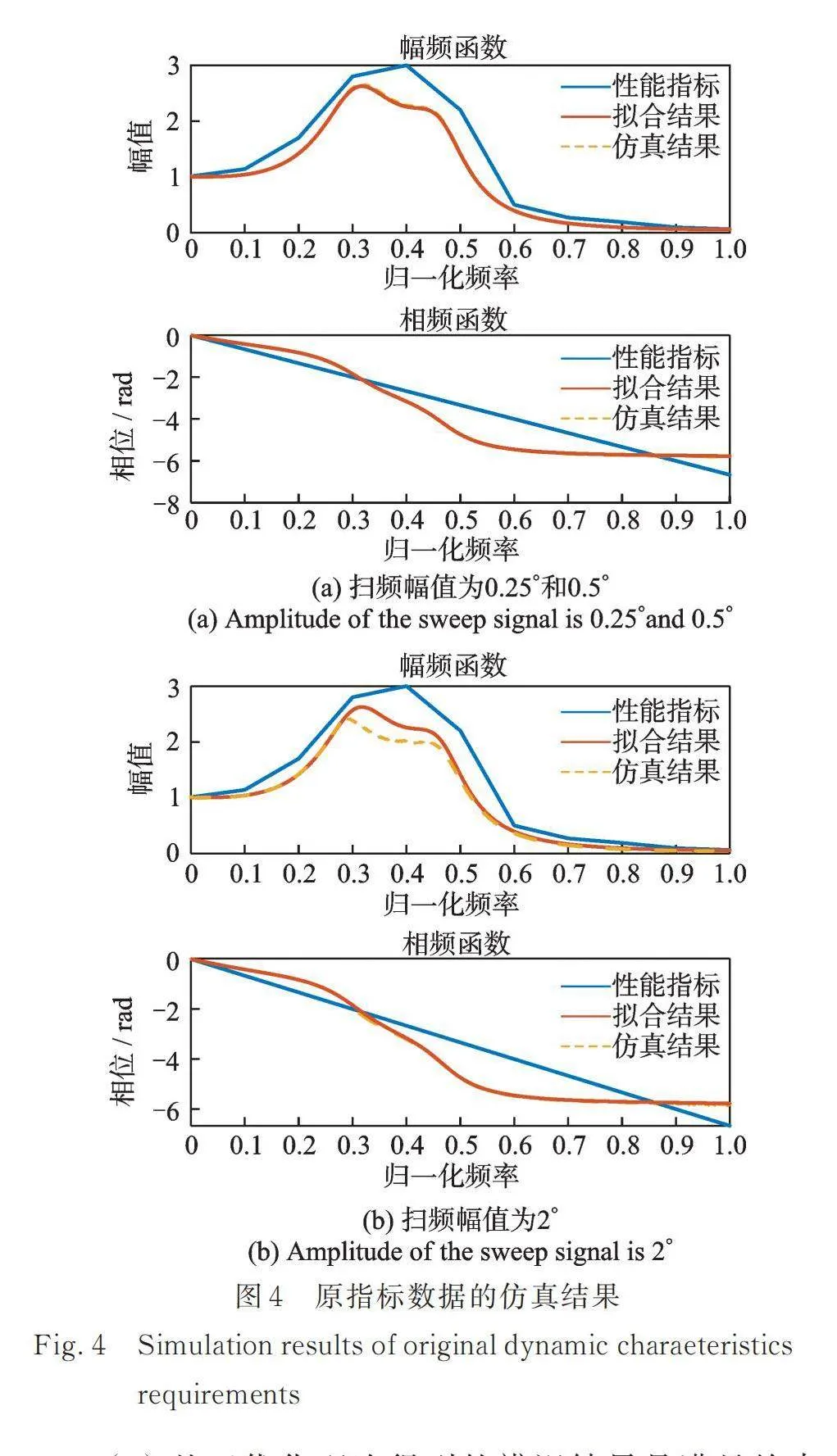
（1） 用補全的動態特性指標數據進行辨識能夠得到滿足指標的PID參數，，，辨識結果分別為665.2，100.3，3.12。將辨識得到的PID參數代入仿真模型進行驗證，結果如圖4所示，其中曲線（擬合結果）為對原指標數據的擬合情況，即辨識得到的PID參數對應的動態特性。掃頻幅值為0.25°和0.5°時，仿真結果與辨識結果吻合良好，此時控制器電壓未飽和，摩擦等非線性因素對幅頻和相頻的仿真結果影響較小，兩個掃頻幅值下的仿真結果幾乎重合；掃頻幅值為2°時，由于控制器電壓飽和，系統飽和非線性對幅頻特性的影響明顯，幅頻仿真數據出現“削峰”現象，但依然滿足指標要求。

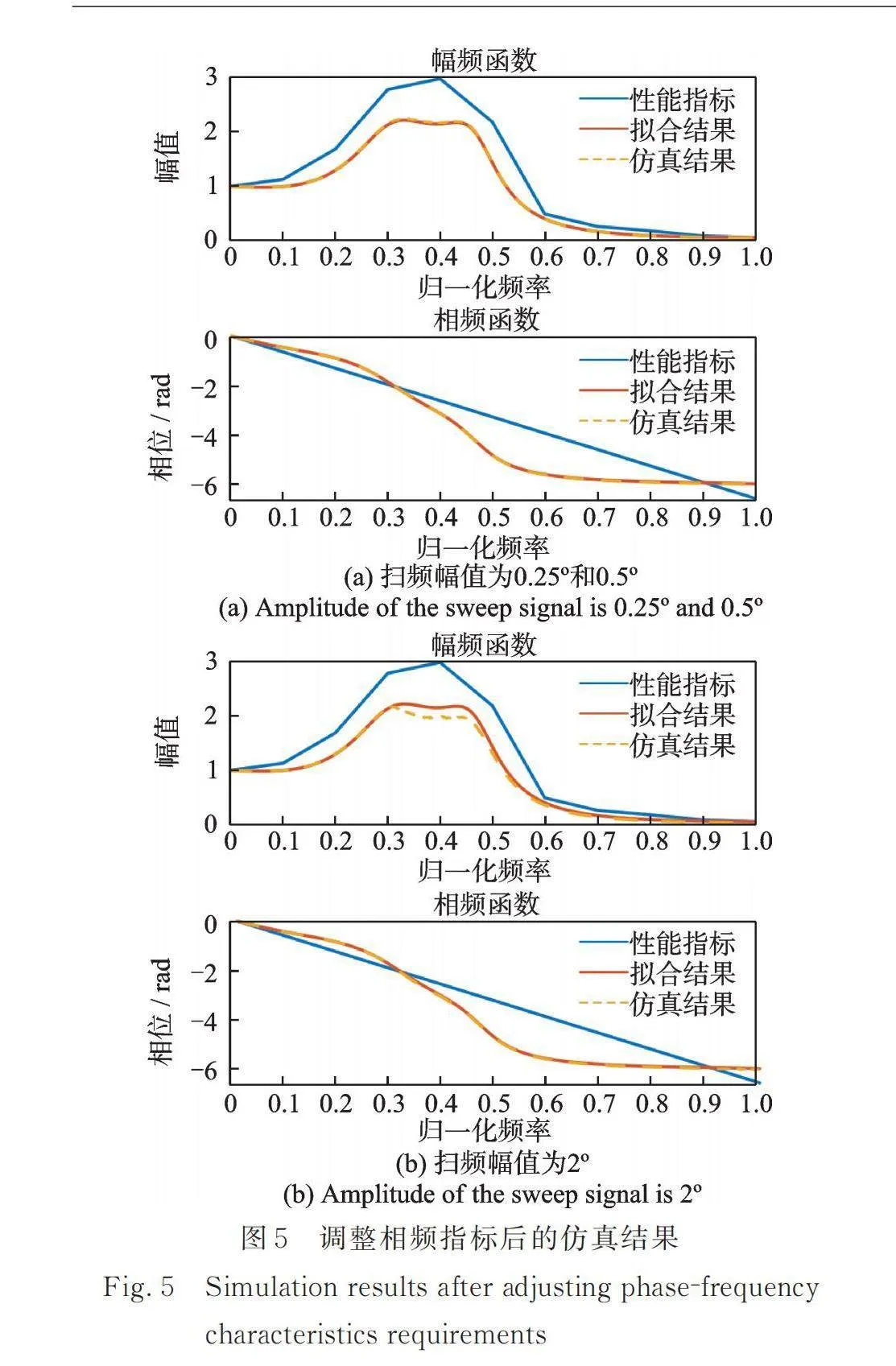
（2） 基于優化理論得到的辨識結果是滿足約束條件下與指標數據誤差最小的一組參數，實際滿足指標的參數可能不止一組，理論上適當調整原指標數據可得到滿足指標的另一組PID參數。調整方法為：通過增大或減小離散頻點上的幅頻和相頻指標數據，直至辨識出滿足原指標要求的另一組PID參數。圖5為在不改變幅頻指標的情況下，將相頻指標的插值斜率增大到原來的1.25倍得到的另一組PID參數的仿真結果，，，的辨識結果分別為584.6，102.1，3.38。掃頻幅值為0.25°和0.5°時，仿真結果與辨識結果吻合良好，兩個掃頻幅值下仿真結果幾乎重合；掃頻幅值為2°時，幅頻仿真數據出現“削峰”現象，依然滿足原指標。

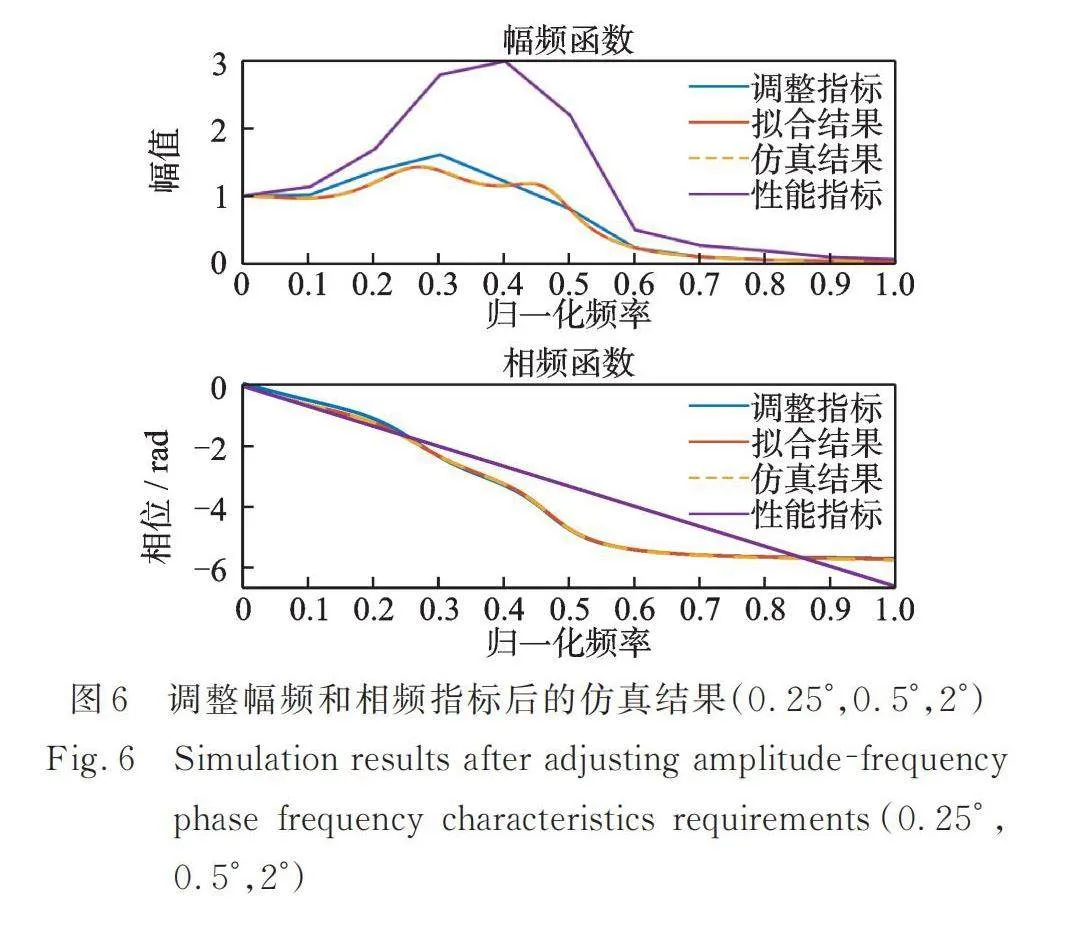
（3） 實際的辨識結果在全頻段內可能不完全滿足指標要求，需要適當調整原指標數據才能得到滿足指標的結果。由于相頻指標只在低頻段內提出，相較于相頻，幅頻更3f380c5ffaa717de74bc562df25534dc容易超出指標。因此，當辨識的結果超過指標時，指標調整依據為：把原幅頻指標數據適當下移，由于相頻數據變化具有相似性，可以用上一步辨識的相頻數據將相頻指標補全，減小補全的相頻數據對辨識結果的影響。如圖6所示，其中曲線（調整指標）為原指標調整后用于辨識的指標數據，相較于原指標，此處幅頻指標在各個頻點上分別下調0.01，0.12，0.32，1.05，1.69，1.35，0.25，0.17，0.13，0.05，0.03。用調整后的指標數據重新進行辨識，，，的辨識結果分別為413.1，37.1，2.04，在幅值為0.25°，0.5°和2°的掃頻指令下均滿足原指標，且控制器電壓未飽和，仿真結果與辨識結果吻合良好，三個掃頻幅值下的仿真結果幾乎重合。相較于圖4和圖5的設計結果，圖6得到的結果非線性影響更小，而且在確保相位滯后滿足性能指標的同時，中低頻段更接近理想的1∶1傳遞。

（4） 由于在設計時加入了傳遞函數系數之間的約束和穩定性約束，設計結果符合位置跟蹤系統的特征，在低頻部分的幅頻傳遞特性趨于1∶1，相位差趨于0。

4 結 論

伺服系統動態特性對飛行器姿態控制設計具有重要影響。本文以機電伺服系統為對象，面向滿足動態特性指標的PID控制設計需求，基于參數辨識思想，提出帶約束的有理分式正交多項式法，完成了PID參數的設計。得到以下結論：

（1） 該方法將系統穩定性要求和傳遞函數系數間的關系表達為曲線擬合的約束條件，使得PID參數設計過程同時兼顧了動態特性指標、系統穩定性和TF系數相容性三方面要求，確保PID控制設計的有效性，提高了設計效率。

（2） 仿真實驗表明，設計結果滿足動態特性指標要求，且通過適當調整擬合指標數據可以得到多組滿足指標的控制器參數，然后，結合動態特性和其他伺服系統特性要求確定最終選擇哪組參數。

（3） 本文的設計方法是面向一般的線性系統提出的。如果伺服系統控制設計需要考慮電流環控制，則只需要在系統動力學模型和傳遞函數中補充電流環環節后，同理采用帶約束的參數辨識方法完成PID參數設計即可。

參考文獻：

［1］朱忠惠，陳孟犖．推力矢量控制伺服系統［M］.北京： 中國宇航出版社，1995．

［2］劉博，祝學軍，南宮自軍，等.電動空氣舵執行機構建模與參數辨識［J］. 宇航學報，2017，38（11）： 1147-1152.

Liu Bo，Zhu Xuejun，Nangong Zijun，et al. Modeling and parameter identification of an aircraft rudder system with an electromechanical actuator［J］. Journal of Astronautics，2017，38（11）： 1147-1152.

［3］呂晨，歐陽權，徐文波，等. 基于干擾觀測器的機電伺服系統PI控制策略［J］. 機床與電液，2024，52（1）：17-22.

Lü Chen，Ouyang Quan，Xu Wenbo，et al. Interference observer-based PI control strategy of electromechanical servo system［J］. Machine Tool & Hydraulics，2024，52（1）：17-22.

［4］張茂盛，段杰，肖息，等. 基于深度強化學習-PI控制的機電作動器控制策略［J］.應用科技，2022，49（4）：19-22.

Zhang Maosheng，Duan Jie，Xiao Xi，et al. Control strategy of electro-mechanical actuator based on deep reinforcement learning-PI control［J］. Applied Science and Technology，2022，49（4）：19-22.

［5］鹿山山，王志勝，歐陽權，等. 飛機機電作動器模糊 PI-ANN復合控制仿真［J］. 兵器裝備工程學報，2021，42（10）： 158-164.

Lu Shanshan，Wang Zhisheng，Ouyang Quan，et al.Simulation of compound control based on fuzzy PI and artificial neural network for aircraft electromechanical actuation systems［J］. Journal of Ordnance Equipment Engineering，2021，42（10）： 158-164.

［6］尚東陽，李小彭，尹猛，等.采用干擾補償模糊整定的雙柔性機械臂抑振策略［J］.振動工程學報，2024，37（1）：1-10.

Shang Dongyang，Li Xiaopeng，Yin Meng，et al. Vibration suppression strategy of dual-flexible manipulator using disturbance compensation fuzzy setting control method［J］.Journal of Vibration Engineering，2024，37（1）：1-10.

［7］Liu H M，Jing J Y，Ma J. Fault diagnosis of electromechanical actuator based on VMD multifractal detrended fluctuation analysis and PNN［J］. Complexity，2018，2018： 9154682.

［8］朱志忠，袁鑫，趙豐，等. 考慮作動器輸出飽合的光電平臺終端滑模神經網絡控制［J］. 振動與沖擊，2022，41（21）：161-167.

Zhu Zhizhong，Yuan Xin，Zhao Feng，et al. Sliding mode neural network control of optoelectronic platform terminal considering actuator output saturation［J］. Journal of Vibration and Shock，2022，41（21）：161-167.

［9］魏澤宇，許文波，張國林，等. 航天機電伺服系統的自抗擾控制［J］. 控制理論與應用，2021，38（1）： 73-80.

Wei Zeyu，Xu Wenbo，Zhang Guolin，et al. Active disturbance rejection control of aerospace electromechanical servo system［J］. Control Theory&Applications，2021，38（1）： 73-80.

［10］趙希梅，陳廣國，金鴻雁. 基于改進灰狼優化算法的PMSM滑模自抗擾控制［J］. 電機與控制學報，2022，26（11）：132-140.

Zhao Ximei，Chen Guangguo，Jin Hongyan. Sliding mode active disturbance rejection control for PMSM based on improved grey wolf optimization algorithm［J］. Electric Machines and Control，2022，26（11）：132-140.

［11］王燁波，劉家輝，衛健，等. 機電伺服系統積分魯棒自適應控制［J］.科技創新與應用，2021，11（23）：7-11.

Wang Yebo，Liu Jiahui，Wei Jian，et al. The integral robust adaptive control of mechatronic servo system［J］. Technology Innovation and Application，2021，11（23）：7-11.

［12］Rubio J. Sliding mode control of robotic arms with deadzone［J］. IET Control Theory&Applications，2017，11（8）： 1214-1221.

［13］張磊，蘇為洲. 伺服系統的反饋控制設計研究綜述［J］. 控制理論與應用，2014，31（5）：545-559.

Zhang Lei，Su Weizhou. Feedback control design of servo systems： a review［J］. Control Theory&Applications，2014，31（5）：545-559.

［14］李璀璀，易文俊，管軍，等. 基于遺傳算法的電動舵機系統模糊PID控制［J］. 兵器裝備工程學報，2021，42（3）：162-167.

Li Cuicui，Yi Wenjun，Guan Jun，et al. Fuzzy PID control of electromechanical actuator system based on genetic algorithm［J］. Journal of Ordnance Equipment Engineering，2021，42（3）：162-167.

［15］陳家俊，賀云波. 伺服系統中PID控制器參數整定的研究［J］. 機床與電液，2021，49（1）：13-16.

Chen Jiajun，He Yunbo. Study on parameter tuning for PID controller in servo system［J］. Machine Tool&Electro-Hydraulic，2021，49（1）：13-16.

［16］Pradhan K S，Subudhi B．Position control of a flexible manipulator using a new nonlinear self-tuning PID controller［J］. IEEE/CAA Journal of Automatica Sinica，2020，7（1）：136-149.

［17］邱亮. 基于階躍辨識的 PID 自整定算法研究及其應用［D］. 上海：上海交通大學，2013.

Qiu Liang. Research and application of PID auto-tuning control method based on step identification［D］. Shanghai：Shanghai Jiao Tong University，2013.

［18］Davanipour M，Javanmardi H，Goodarzi N. Chaotic self-tuning PID controller based on fuzzy wavelet neural network model［J］. Iranian Journal of Science and Technology，Transactions of Electrical Engineering，2018，42（3）：357-366.

［19］李建明，蔣孟龍，安林雪，等. 機電作動器動力學建模與電流跳變現象分析［J］. 電機與控制學報，2020，24（1）：104-110.

Li Jianming，Jiang Menglong，An Linxue，et al. Dynamic modeling and current jump analysis of electro-mechanical actuator［J］. Electric Machines and Control，2020，24（1）：104-110.

［20］Falangas E T. Performance Evaluation and Design of Flight Vehicle Control Systems［M］. Hoboken，New Jersey：Wiley，2015.

［21］Richardson M H，Formenti D L. Parameter estimation from frequency response measurements using rational fraction polynomial［C］∥ Proceedings of the International Modal Analysis Conference&Exhibit，1982： 167-182．

Design method of PID control for electromechanical servo system based on dynamic characteristics requirements

CHEN Guo-rong，NANGONG Zi-jun，LIU Bo

（China Academy of Launch Vehicle Technology，Beijing 100076，China）

Abstract： In order to solve the problem that it is difficult to fully consider the dynamic characteristics （amplitude-phase frequency characteristics） requirements in the PID parameter design of electromechanical servo system，a PID design method for dynamic characteristics is proposed. The 9-order Transfer Function （TF） model of electromechanical servo system is established based on dynamic equation. The relationship between Routh criterion and TF coefficient is used to supplement the stability constraint of the system and the compatibility constraint of TF coefficient to ensure the stability of the system and the compatibility of TF coefficient in the PID design process. On this basis，based on the idea of parameter identification，the rational fraction orthogonal polynomial method is used to identify the coefficients in the TF model，so that the PID parameters are quickly determined，which improving the design efficiency，and multiple groups of controller parameters that meet the original index can be identified by adjusting the index data. The simulation results show that the designed PID parameters not only meet the requirements of dynamic characteristics，but also take into account the compatibility of system stability and TF coefficient. The design results are in good agreement with the simulation experiments.

Key words： PID control；parameter identification； electromechanical servo system；dynamic characteristics requirements

作者簡介： 陳國榮（1999―），男，碩士研究生。電話： （010）88520510； E-mail：chen_gr1111@163.com。

通訊作者： 南宮自軍（1968―），男，博士，研究員。電話： （010）68758120； E-mail：nangongzijun@yeah.net。