小學數學新增“尺規作圖”內容的課程價值

【摘 要】《義務教育數學課程標準（2022年版）》在小學階段的第二和第三學段新增了“尺規作圖”的內容。通過對尺規作圖源流的考察，可以發現尺規作圖過程中蘊含著嚴謹的推理和豐富的想象，將其應用于探索性學習活動的設計，對于發展學生數學的眼光、數學的思維以及數學的語言具有特殊的課程價值。同時，小學階段尺規作圖的教育價值還體現在其基礎性上，為學生后續的數學學習奠定堅實的基礎。

【關鍵詞】尺規作圖；推理；想象；課程價值

《義務教育數學課程標準（2022年版）》（以下簡稱“2022年版課標”）在小學階段的第二和第三學段新增了“尺規作圖”的內容，一線教師在教學中面臨的問題有：如何理解這一內容及其課程價值？如何在教學中實現這些課程價值？尺規作圖在數學史上具有悠久的歷史，其相關內容極為豐富，并貫穿于多個學段的課程內容之中，小學階段的教學如何凸顯其基礎性？本文將圍繞上述問題展開討論。

一、背景

“尺規作圖”的起源可追溯到古希臘歐幾里得（Euclid，約公元前330年—公元前275年）的《幾何原本》。在當時，人們認為直線與圓（球）是構成世界萬物最基本、最完美的圖形，因此，他們期望通過使用制作直線與圓的簡單工具，通過推理與想象去建構并描繪無限的世界。以柏拉圖（Plato，公元前427年—公元前347年）為代表的唯心主義哲學家，不相信直觀所見的真實，他們認為感觀所見的、暫時的、不完美的世界必須被抽象的、永恒的、完美的世界所取代［1］。

《幾何原本》秉承并沿襲這樣的思想，強調所有的命題都應基于已知為真的命題進行推演，因此需要確立最初的邏輯起點。在《幾何原本》的第一卷中，開篇闡述了23個定義（Definition）、5條公設（Postulate）和5條公理（Axiom）。定義指的是所用術語的意義，例如，定義15：“圓由一條線包圍著的平面圖形，其內有一點與這條線上任何一個點所連成的線段都相等。”定義20：“三角形中，三條邊相等的稱等邊三角形，兩條邊相等的稱等腰三角形，各邊都不相等的稱不等邊三角形。”分別描述了圓以及等邊三角形、等腰三角形、不等邊三角形的概念。

公理與公設則是不證自明、公認為正確的命題，二者的區別在于普適性的差異。公理不僅適用于幾何領域，也適用于其他科學領域，因此公理也被稱為“共通觀念（Common Notions）”。例如，第一條和第二條公理描述了量與量之間的相等關系。

l公理1：等于同量的量彼此相等。

l公理2：等量加等量，其和仍相等。

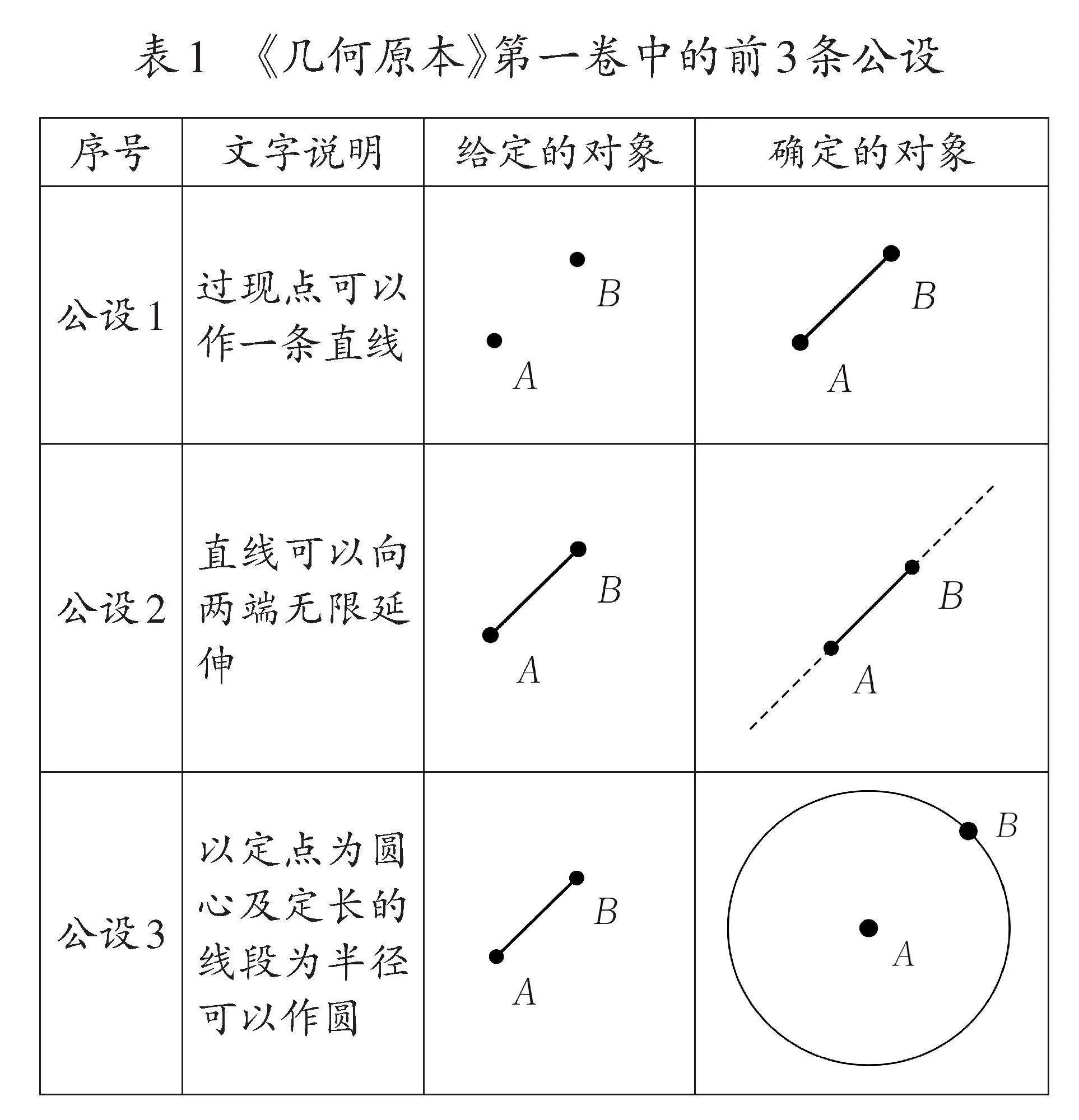
公設則是幾何學內部不證自明的事實，與尺規作圖直接相關，它規定了如何從給定的對象構造出確定的對象。例如，《幾何原本》第一卷中的前3條公設如表1所示。

綜上所述，《幾何原本》第一卷中的定義、公設和公理構成了使用直尺和圓規作基本圖形的基礎。定義指向概念的意義，公設說明了如何作圖，而公理則解釋了為什么這樣作圖是正確的1。如果將尺規作圖視為一種游戲，那么定義、公設和公理就是游戲過程中必須遵守的規則，正是這些規則確保了尺規作圖成為一個嚴謹的推理過程。下面，以2022年版課標中的例26為例，詳細闡釋這一推理過程。

二、嚴謹的推理

2022年版課標中的例26所提及的“作一個給定邊長的等邊三角形”，實際上是《幾何原本》第一卷中的第一個命題。該命題在不同中文譯本中的表述存在差異，現將兩種表述列舉如下：

l表述1：已知一條線段可以作一個等邊三角形。［2］

l表述2：在一個已知有限直線上作一個等邊三角形。［3］

二者的區別在于，是否將給定線段作為所作等邊三角形的一條邊。兩種中譯本都依據同一英文底本，即英國科學史學家希思（Thomas little Heath，1861—1940））的英譯評注本《歐幾里得原本13卷》，其中命題1的英文表述為：“On a given finite straight line to construct an equilateral triangle.”［4］

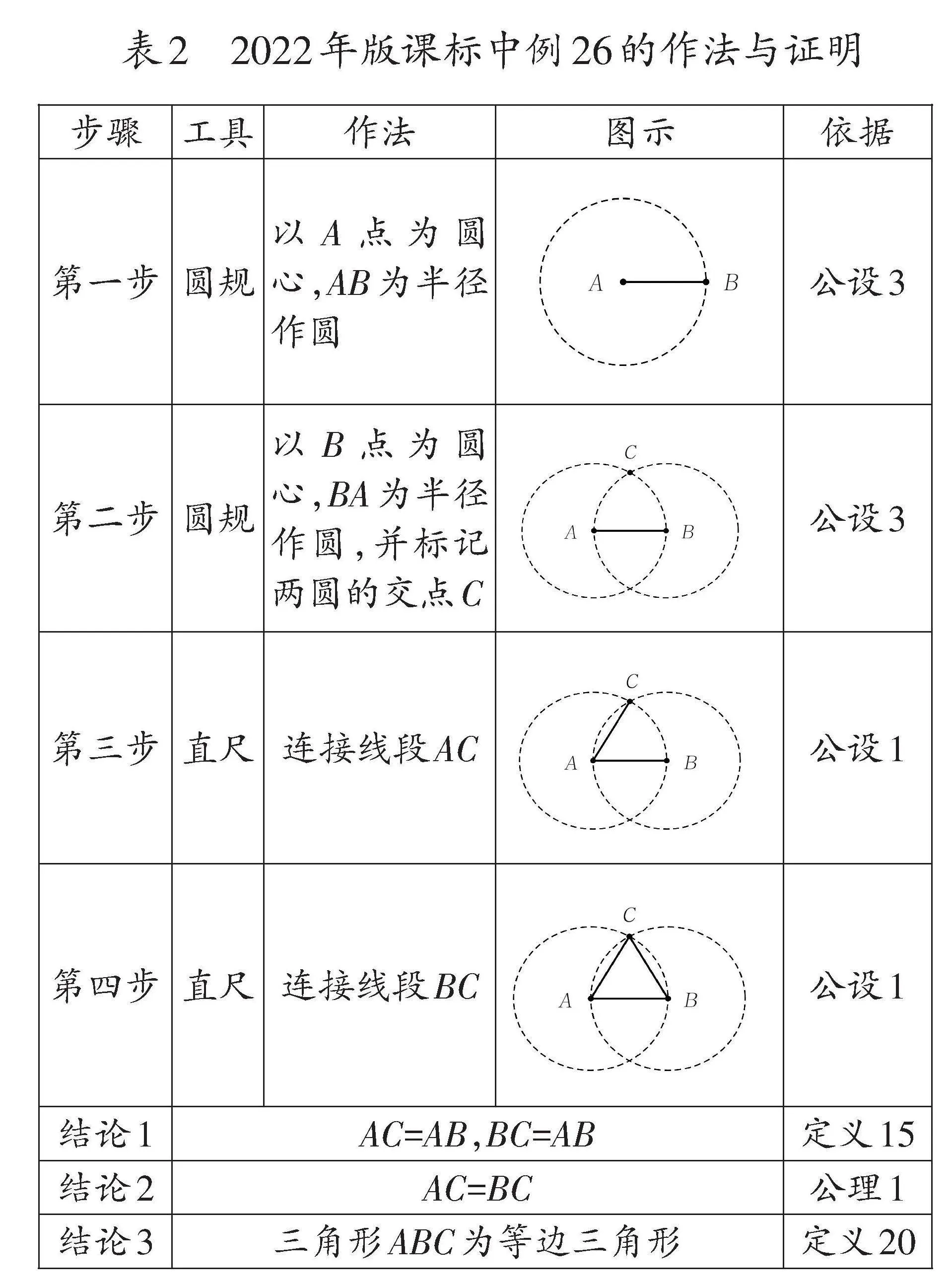
《幾何原本》第一卷中的命題1可以理解為：若給定一條線段，那么可利用這條線段作為三角形的一條邊，進而作出另外兩條等長的邊，形成等邊三角形。構造過程的每一步是否可行及正確，都需依據定義、公設或公理進行驗證。為了清晰描述這一過程，采用表格的形式進行展示（如表2）。

推理的最終結論是“三角形ABC為等邊三角形”，為此必須闡明三角形的三條邊是否存在，以及為什么相等。推理過程包括四個操作步驟和三個作為結論的判斷，每一步操作需說明為什么可行的依據，每一個結論都需理由作為依據以闡明為什么正確。因此，可以說尺規作圖的過程本質上是推理過程，推理的嚴謹性體現為“言必有據”，表2右側列出的依據均源自事先規定的定義、公設和公理，因此可以相信最終結論的正確性。

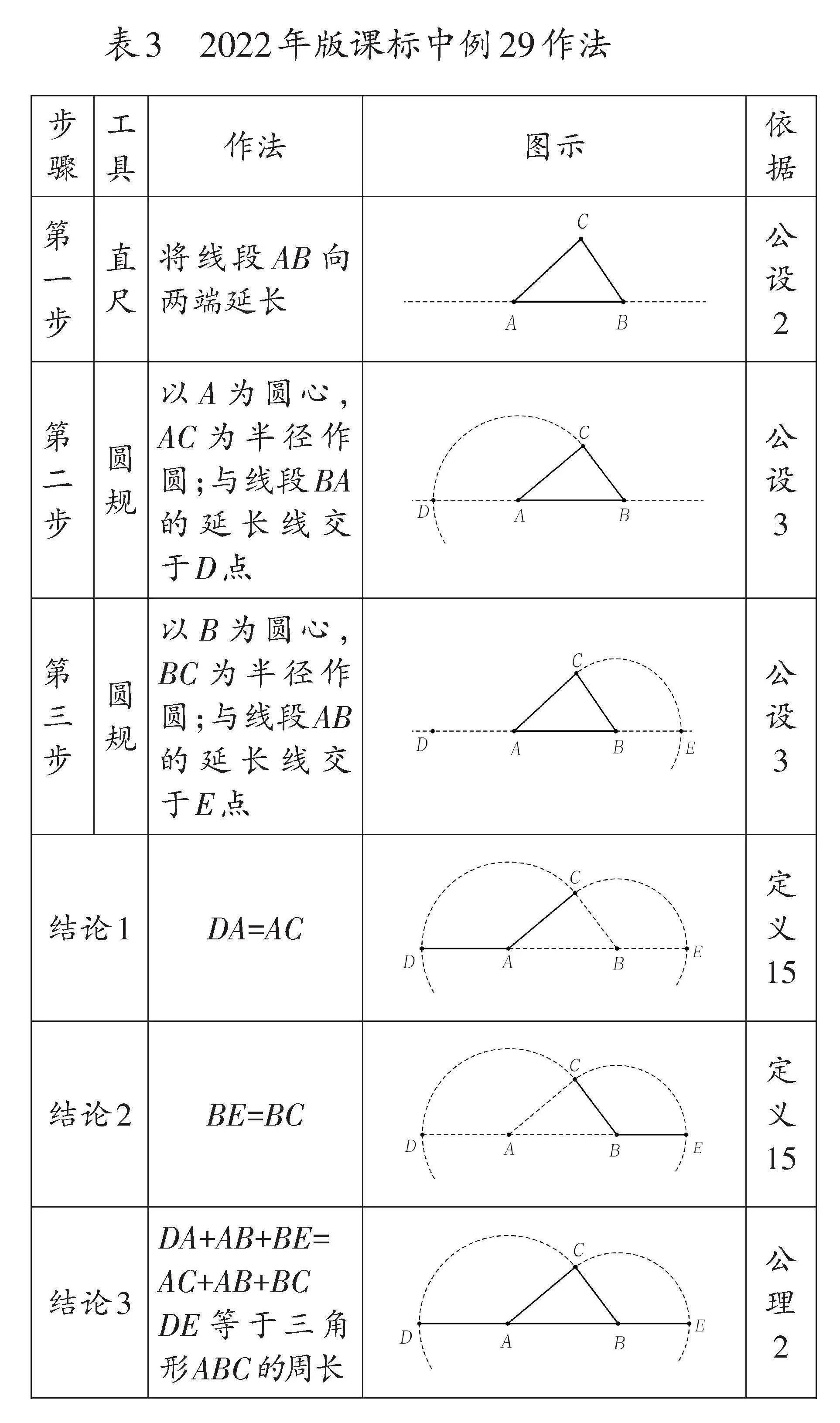
對上述過程稍加變化，能夠實現2022年版課標中例32的“給定三條線段作三角形”的作法，其中包括對三角形三邊關系的探討（限于篇幅，讀者可自行完成詳細的作圖和證明過程）。所有這些均屬于“給定線段作三角形”的問題范疇。將此過程逆向操作，便成為2022年版課標中例29的作圖問題：“把三角形的三條邊依次畫到一條直線上。”下面用表3詳細展示這一作圖過程。

表3中的作圖過程與表2略有不同，其中第一步“將線段AB向兩端延長”的依據是“公設2”；結論3中DE的長度等于三角形的周長，其依據為“公理2”。

綜上所述，尺規作圖的過程實際上是一個嚴謹的推理過程。從教育的角度來看，這種推理無疑有助于培養學生邏輯思維和論證習慣。然而，也應注意這種嚴謹性可能帶來的問題。表2與表3中的作圖及證明過程具有明顯的形式化與程序化特征，只要遵循“模仿記憶、按部就班、依次執行”的原則，便能確保無誤。這種嚴謹性可能會對教學產生消極影響，教師的“教”可能簡化為“講解—示范—留作業”，學生的“學”自然成為“傾聽—模仿—做練習”，從而使得尺規作圖變成一種無理解的操作過程。因此，在將尺規作圖納入數學課程與教學時，應避免僅注重推理的嚴謹性，同時應充分彰顯其開放性的特征，引導學生發揮豐富的想象進行探索。

三、豐富的想象

2022年版課標中的例26特別強調：“（尺規作圖）教學中，可以讓學生發揮想象力，用直尺和圓規構建各種可以實現的圖形。”這表明尺規作圖不僅是嚴謹的推理過程，也是發揮想象力、進行探索的過程。因此，對尺規作圖的作法和結果，教師應持有開放性的認識，即“作法未必唯一，結果可以拓展”。

“作法未必唯一”意味著作圖的過程和方法具有多樣性。在數學的歷史發展中，許多數學家對尺規作圖方法的多樣性進行了深入探索。比如17世紀丹麥幾何學家喬治·摩爾（Georg Mohr，1640—1697）與18世紀意大利數學家洛倫佐·馬斯凱羅尼（Lorenzo Mascheroni，1750—1800）分別獨立發現并證明了一個結論：每一個能夠用直尺和圓規作出的圖形都可以摒棄直尺，僅用圓規作出。這一發現后來被稱為“摩爾-馬斯凱羅尼定理（Mohr-Mascheroni Theorem）”［5］，當然這些內容已經超出了小學數學課程的范疇。下面重點談談尺規作圖結果的拓展性。

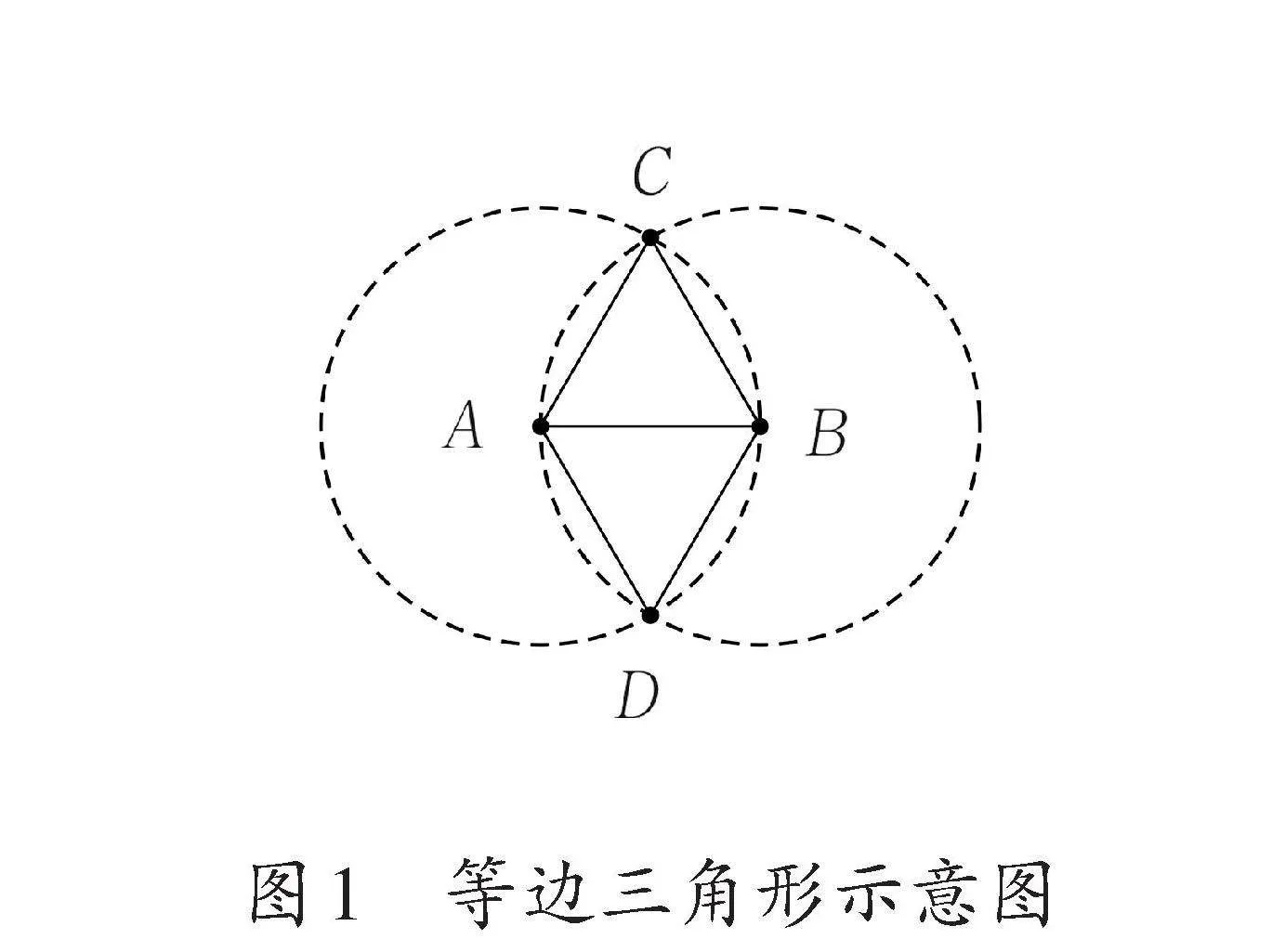
尺規作圖結果的拓展性至少體現在兩個方面：一是“目標圖形未必唯一”；二是“最終結論可以延伸”。以2022年版課標中的例26為例，目標圖形等邊三角形并非唯一，還可以作出與三角形ABC關于線段AB對稱的另外一個等邊三角形ABD（如圖1）。

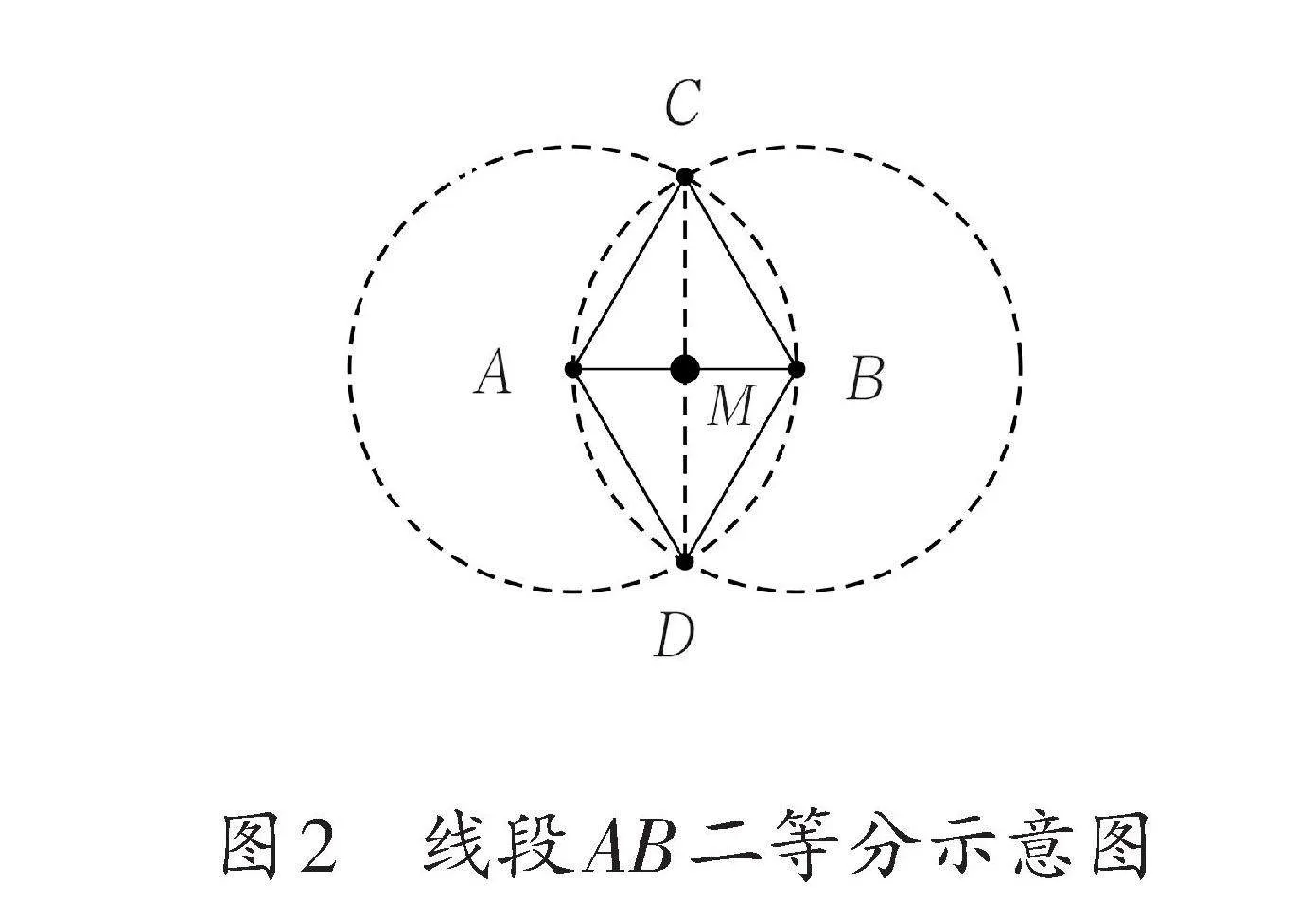
基于這樣的作圖結果，通過進一步的想象，可以使得最終結論得以延伸。從點C向點D作出線段CD，將會與線段AB形成一個交點M，直觀上可以看出這個點是線段AB的中點（小學階段依靠直觀看出即可），實現了將一條線段平均分為兩段，即M點將線段AB二等分（如圖2）。

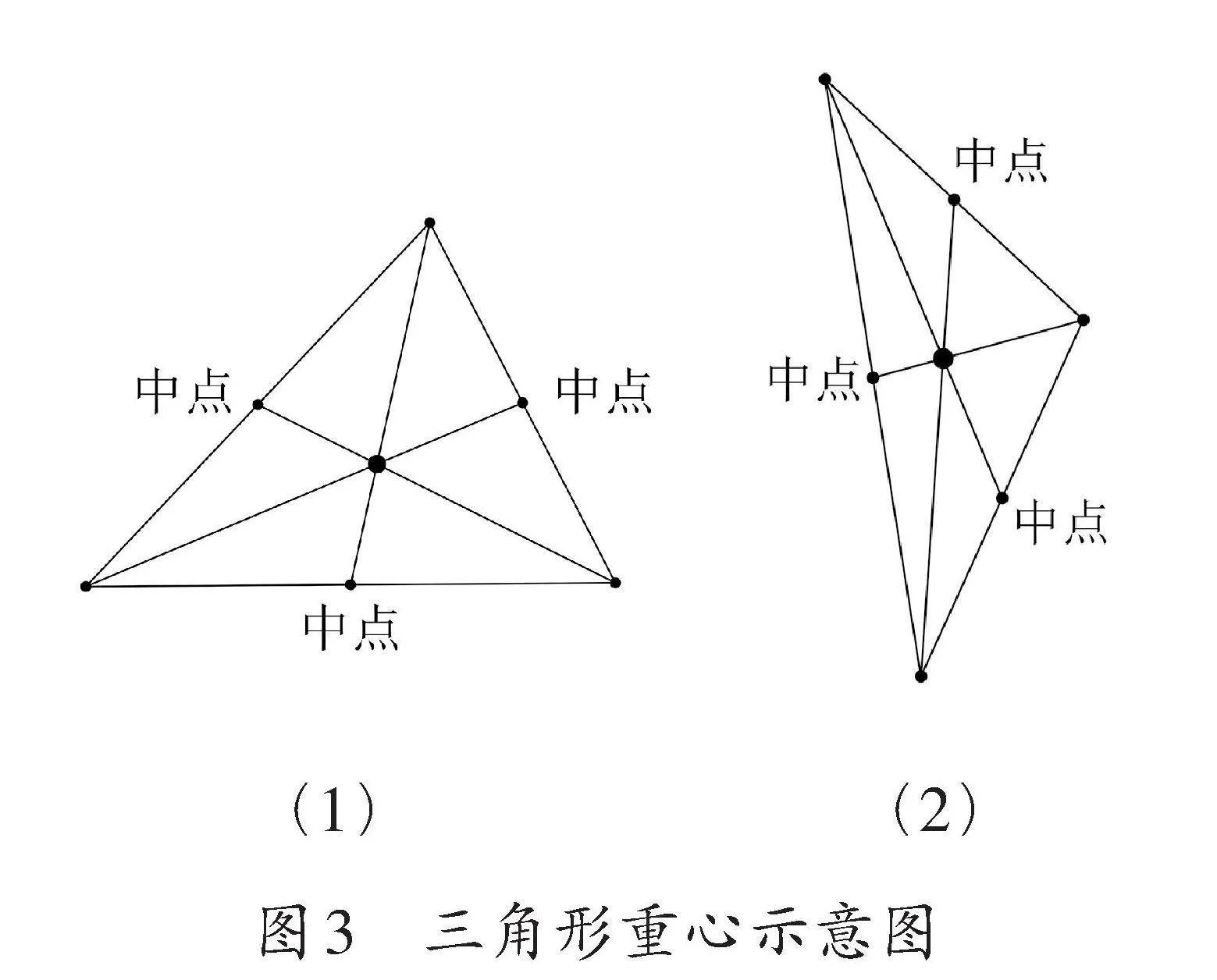
如果將線段二等分或在線段上確定中點視為“基本作圖”，則可以以此為邏輯起點，進一步探索幾何圖形的諸多性質。例如，對于任意大小、形狀各異的三角形，在其三邊上分別作出中點，并將這些中點與對面頂點相連，可以發現這三條線段相交于同一點（如圖3）。

這樣三線共點的“點”也叫三角形的重心（又叫質心），是中學數學與物理課程的重要內容。因此，學生在小學階段經歷尺規作圖的探索，對于與中學課程內容的銜接具有積極意義。

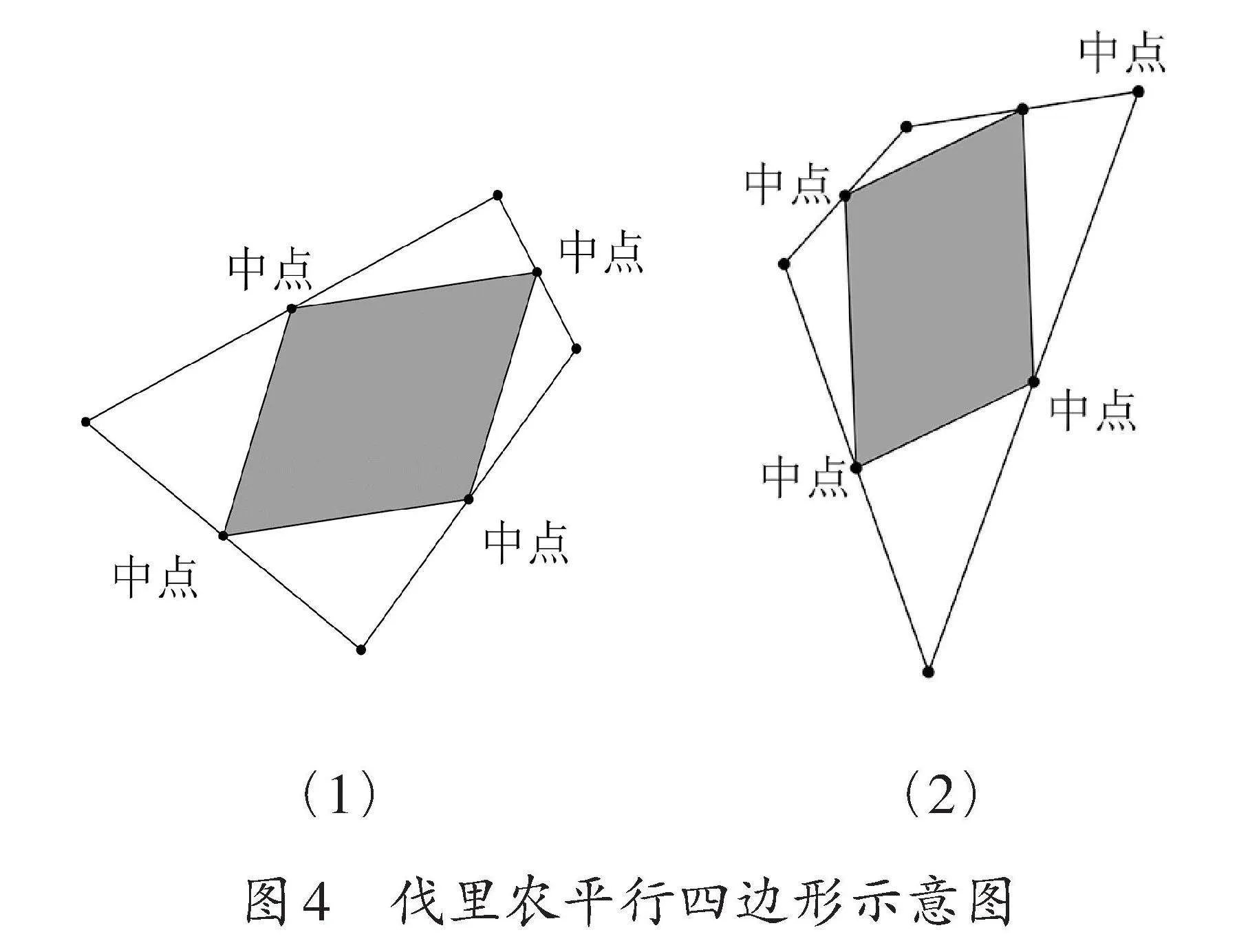
再以17—18世紀法國數學家、物理學家皮埃爾·伐里農（Pierre Varignon，1654—1722）發現的著名結論為例：在任意四邊形四條邊上分別作出中點，并用線段連接，構成一個內部的四邊形，無論原來四邊形是什么形狀，該內部的四邊形一定是平行四邊形［6］（如圖4）。

此類現象揭示了“變中的不變”的規律性，通常所說的“探索規律”實質上是在千變萬化的現象中發現這種“變中的不變”的規律［7］。因此，在教學中引導學生發揮想象力對目標圖形和最終結論進行延伸，實際上是在經歷探索規律的過程。

綜上所述，簡單的“線段二等分”作圖可應用于多種幾何圖形性質的探索，這種應用性可視為作圖結果的“延伸”，即拓展性的縱向向度。除此之外，還可從橫向向度對作圖結果進行“延展”：既然給定一維的線段可以利用尺規作圖二等分，那么是否可以三等分、四等分……同樣，對于平面圖形（如三角形、長方形、平行四邊形等）的面積以及平面中的一個角，是否可以通過尺規作圖實現類似的等分？

在教學中，引導學生發揮想象力，經歷此類縱向的延伸與橫向的延展的拓展性思考，不僅有助于學生對于相關課程內容的認識與理解，同時使得數學課程內容超越教材的局限，為學生發揮想象力提供廣闊的空間和無限的可能性。

四、小學階段“尺規作圖”的基礎性

如前所述，尺規作圖歷史悠久、源遠流長、內容豐富，其中蘊含著嚴謹的推理和豐富的想象。這無疑可以作為尺規作圖的教學目標。同時，教師應當重視小學階段尺規作圖的基礎性，主要體現在對作圖工具的全面認識與熟練使用上。

在尺規作圖中，“直尺（Straightedge）”與如今用于測量長度的“尺子（Ruler）”有所不同，直尺是無刻度的，僅用于構造直線或線段，不具備測量長度的功能，因此尺規作圖的過程不涉及數值及其計算，而是純粹的幾何形與量的構造過程。

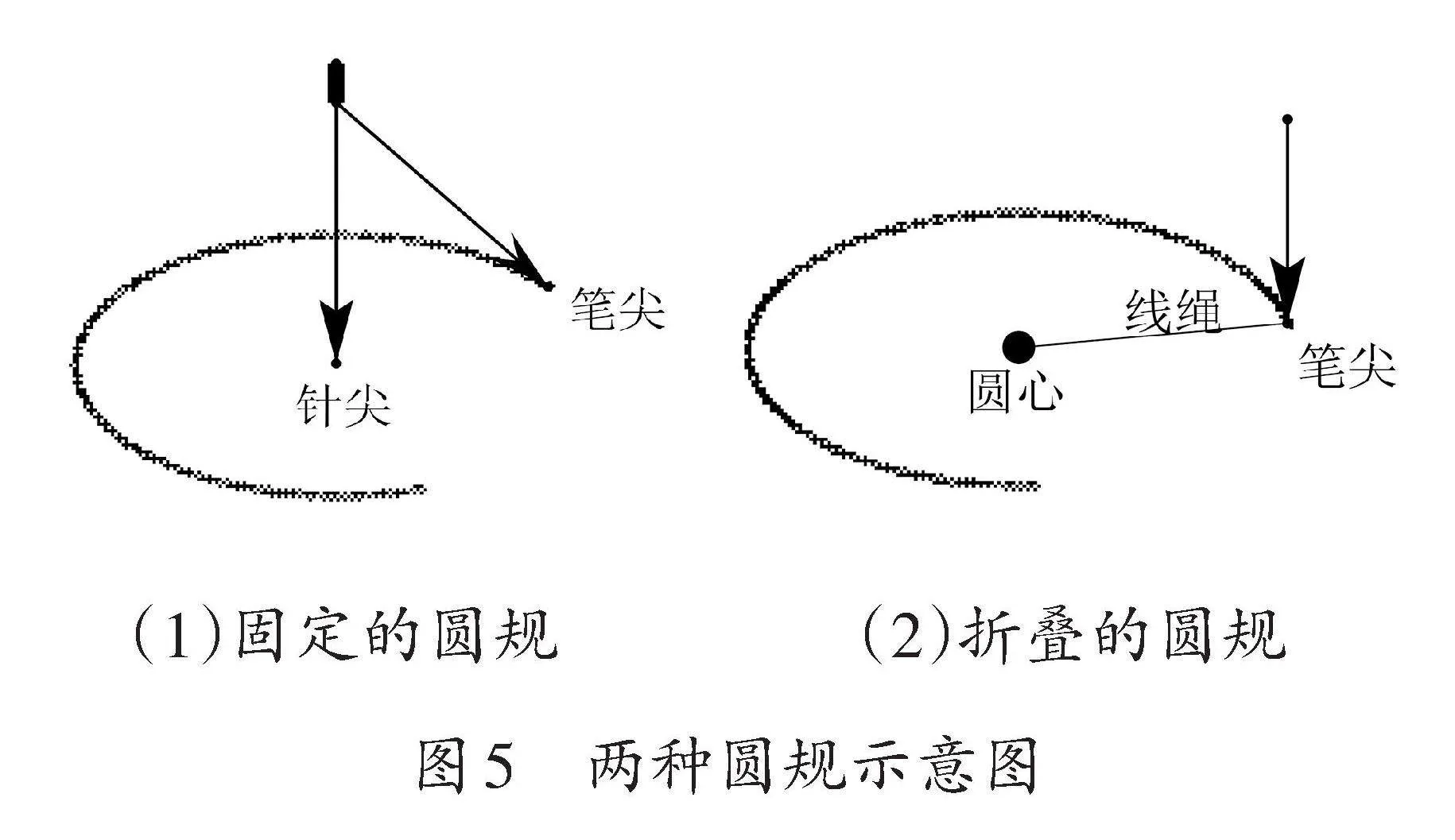
古希臘時期的圓規與現代圓規也有區別，現代圓規由三個部分組成：一是固定圓心的針尖；二是用于描繪軌跡的筆尖；三是可以調整針尖與筆尖距離的裝置，即圓的半徑。這種圓規具有準確調整與確定半徑的特點，其對應的英文名稱為“Fixed Compass（中譯：固定的圓規）”，如圖5（1）所示。古希臘時期的圓規是由線繩捆綁筆尖形成的，作圓時需固定線繩的某一點作為圓心，然后旋轉筆尖描繪圓的軌跡，其特點是難以精確確定圓心到筆尖的距離（即半徑），這種圓規的英文名稱為“Collapsing Compass（中譯：折疊的圓規）”［8］，如圖5（2）所示。

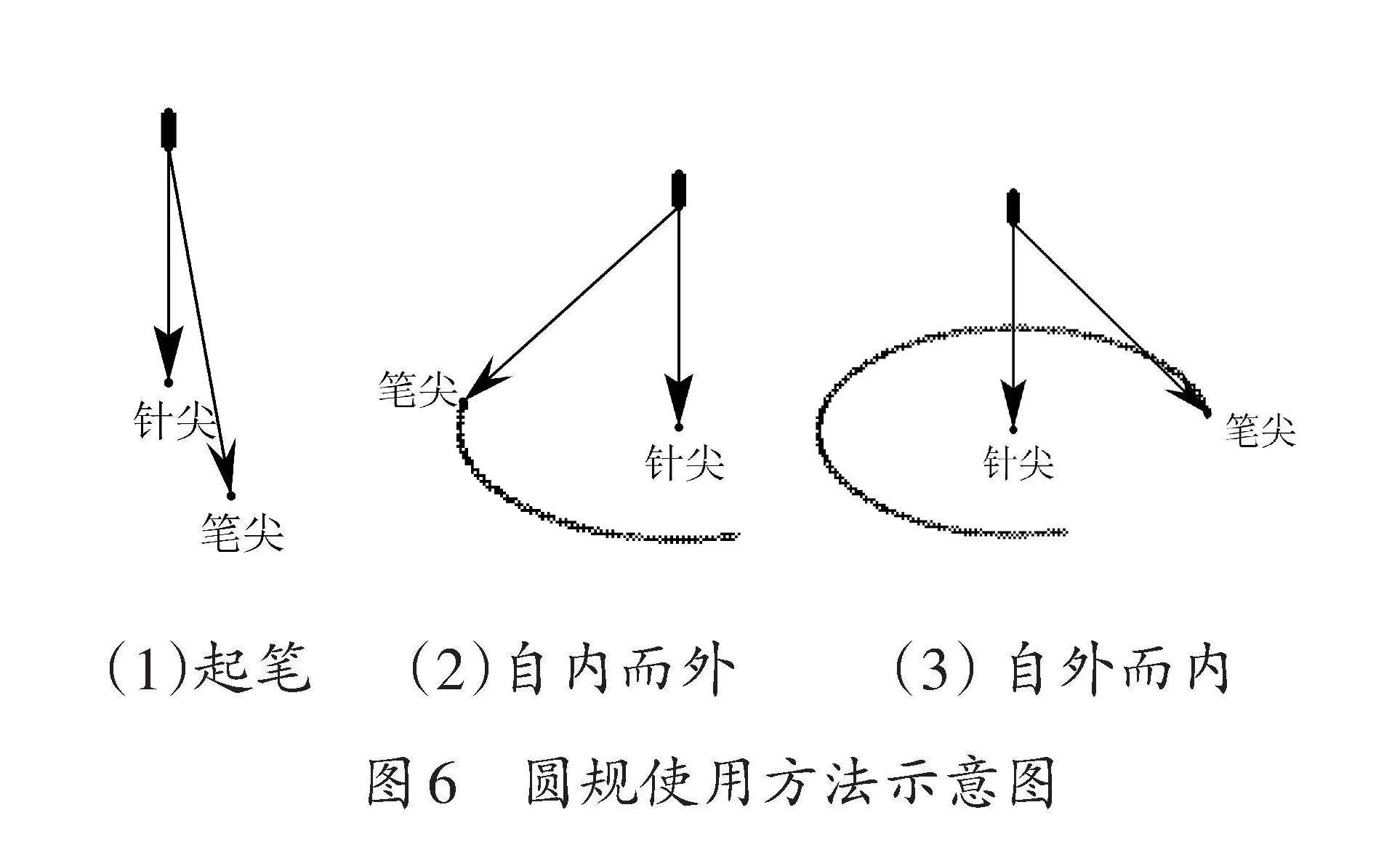
小學尺規作圖教學的初始階段，首先應安排“認識直尺和圓規”的教學環節，讓學生通過操作活動對不同直尺和圓規進行比較，從而發現它們的異同。在圓規的使用教學中，應注意引導學生探索“一筆畫出”整個圓的方法，這主要JzeKpQBMhhA0uAdTZpj19A==包括起筆位置和筆尖的運行方向。通常的做法是從靠近身體的位置起筆，沿著順時針方向旋轉筆尖，“先自內而外，再自外而內”（如圖6）。

在認識直尺和圓規的基礎上，就需要通過經常性的練習逐步達到熟練使用的目的。為了實現經常性的練習，可以將直尺和圓規視為具身學習活動的學具，將其應用于教科書中相關內容的教學。如在2022年版課標的第29頁、第30頁和第35頁分別提及了小學階段尺規作圖的相關內容，并附有相應的例題（如表4）。

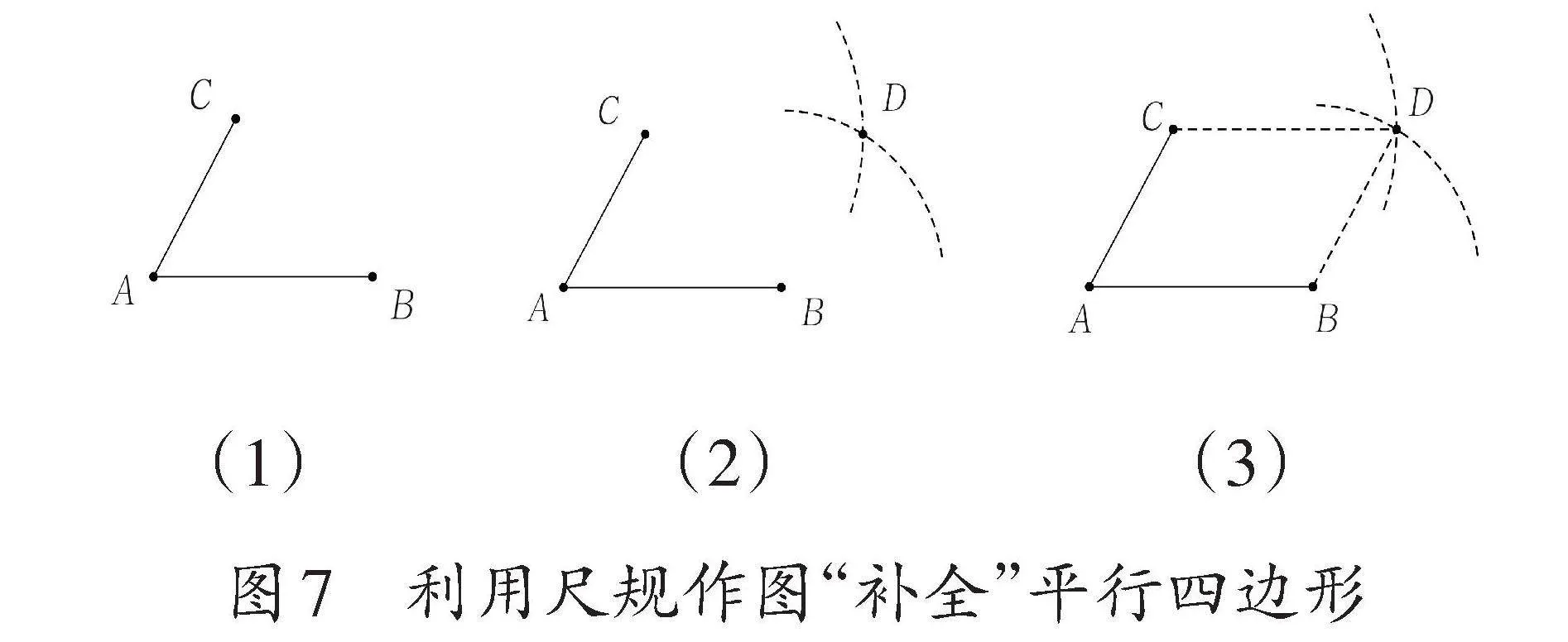
實際上，小學數學課程中還有許多其他內容同樣適合用尺規作圖進行教學。以“平行四邊形的認識”為例，如果提供一個不完整的平行四邊形，如圖7（1）所示，即給定兩條邊及其夾角，讓學生利用尺規作圖來“補全”平行四邊形。

學生只需“以B為圓心，AC為半徑”以及“以C為圓心，AB為半徑”分別作圓（只需作出局部圓弧），便能找到兩個圓的交點D，如圖7（2）所示。接著，使用直尺連接CD和BD，即可實現“補全”平行四邊形，如圖7（3）所示。在作圖過程中，通過圓的半徑處處相等的特性，學生能夠直觀感受到平行四邊形對邊相等的性質。

總之，尺規作圖不僅是畫圖，其英文表達為“Geometric Construction（中譯：幾何建構）”，這里的“建構（Construction）”包含雙重含義：其一，是基于對現實世界事物的感知和想象，在思維中構建圖形；其二，是將思維中的圖形通過直尺和圓規的使用轉化為可視化的圖像，從而實現抽象思維的具體化。因此，尺規作圖在溝通現實世界與思維世界之間起到了橋梁的作用，它既是對現實世界具體事物的抽象化，又是將思維中的抽象圖形具體化的過程。作圖過程中所蘊含的思維活動，既有嚴謹的推理，也有豐富的想象。將尺規作圖應用于探索性學習活動的設計，對于發展學生數學的眼光、數學的思維以及數學的語言具有特殊的課程價值。同時，尺規作圖的教育價值還體現在其基礎性上，小學階段全面認識并熟練使用作圖工具，為后續的數學學習奠定堅實的基礎。

參考文獻：

［1］克萊因.西方文化中的數學［M］.張祖貴，譯.北京：商務印書館，2013.

［2］歐幾里得.幾何原本［M］.燕曉東，編譯.北京：人民日報出版社，2005.

［3］歐幾里得.幾何原本［M］.蘭紀正，朱恩寬，譯.西安：陜西科學技術出版社，2003.

［4］HEATH T L. The thirteen books of Euclid’s Elements（Vol.1）［M］. New York：Dover Publi cations，1956：276.

［5］MARTIN G E. Geometric constructions［M］. Berlin：Springer，1998：53.

［6］OLIVER P N. Pierre Varignon and the parallelogram theorem［J］. The mathematics teacher，2001，94（4）：316-319.

［7］郜舒竹.“探索規律”釋義［J］.課程·教材·教法，2015，35（1）：102-107.

［8］BEN-ARI M. Mathematical surprises［M］. Heidelberg：Springer，2022：2.

（首都師范大學初等教育學院）