設計游戲活動助力學生推理能力提升的實踐

【摘 要】在數學游戲課中，教師要將數學問題融入游戲之中，能讓學生在主動參與游戲活動的同時，潛移默化地學習數學知識和數學思想方法。以二年級數學游戲“兔媽媽的格子菜地”為例，教師在對游戲原理進行解讀，對游戲內容進行分析的基礎上，通過創設問題情境，設置游戲進階升級關卡，引導學生主動參與游戲，經歷思考過程，積累活動經驗，發展數學思維。

【關鍵詞】數學游戲；數方；推理意識；空間想象力

在數學游戲課中，教師要將數學問題融入游戲之中，能讓學生在主動參與游戲活動的同時，潛移默化地學習數學知識和數學思想方法。如何選擇合適的學習素材，能夠將游戲的樂趣與數學的學習深度融合，助力學生推理能力的提升？如何將學生對游戲的熱情轉化為數學學習的動力？筆者以二年級數學游戲“兔媽媽的格子菜地”為例進行探討。

一、游戲解讀與教學分析

（一）游戲原理解讀

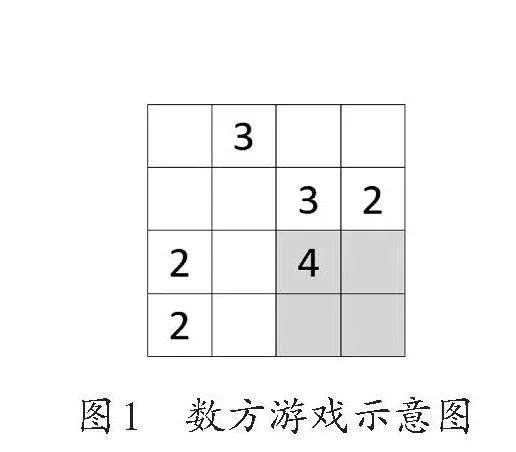
數學游戲“兔媽媽的格子菜地”源自數方游戲。數方是一種邏輯解謎游戲，將數字與圖形緊密結合，游戲過程富有挑戰性，主要鍛煉玩家的邏輯思維能力、計算能力和空間想象能力，是一款體現數形結合思想的邏輯游戲。游戲的道具是長方形（或正方形）格子圖，圖中散布著若干數字（如圖1）。游戲規則要求玩家將所有格子劃分為若干個長方形或正方形區域，每個數字代表其所在區域內小方格數量，且同一個格子不能被重復劃分。玩家需通過邏輯推理，根據數字確定每個區域的形狀及位置，最終完成整個長方形（或正方形）格子的劃分。

例如，在圖1所示的4×4的格子上，玩家可以將最大的數字4作為突破口，確MA5ji/gvD5KdWELcdK6RrItwYxLRy2b+Nf2mKheAWzE=定4所在的區域只能是正方形而不能是長方形，接著根據其他數字依次推理劃分，直至整個大正方形被完整分割。

（二）游戲內容分析

1.創設富有童趣的游戲情境

二年級學生的思維特點以形象直觀為主。因此，筆者為數方游戲設計了“兔媽媽分菜地”的游戲情境，以輕松有趣的動物故事激發學生解決問題和挑戰問題的興趣。

2.結合已有知識經驗的應用

學生在一年級已經初步了解了長方形和正方形的特征，并在二年級學習了表內乘法。因此，在游戲教學中，教師引導學生將數字與形狀相結合，在動手操作中識別不同的幾何形狀，感知不同形狀在格子中的排列和組合，理解長方形、正方形與格子數之間的對應關系。例如：數字4可能對應4×1的長方形或2×2的正方形；數字6可能對應6×1或3×2的長方形等。通過觀察和操作，將抽象的數字與具體的幾何形狀聯系起來，有助于培養學生的空間觀念。

3.設置具有挑戰的游戲層階

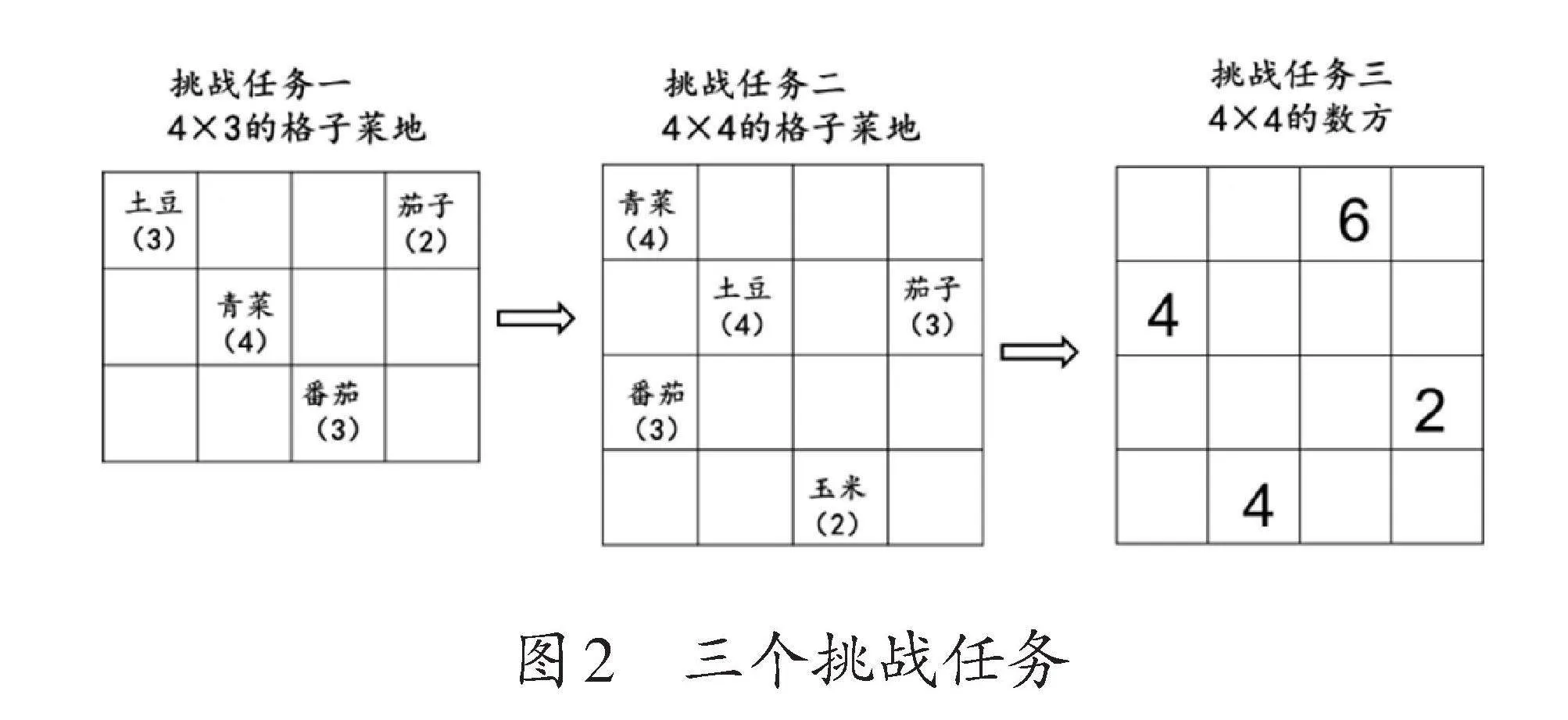
作為一款游戲，層階性的挑戰闖關是不可或缺的。這不僅能夠激發學生的好奇心和求知欲，而且能在有趣好玩的過程中培養學生的推理意識。因此，在明確游戲規則后，教師引導學生嘗試操作，并設計了一個活動和三個挑戰任務（如圖2）。

在游戲活動中，學生通過觀察信息，分析信息，應用信息，邊操作邊概括總結求勝策略。將最大數或邊角上的數作為突破口，觀察并找到形狀唯一的圖形；面對多種可能性時，先假設再排除，運用“假設—嘗試—調整”的策略，直到挑戰成功，從而培養邏輯推理能力。

基于上述理解，確立如下教學目標：

（1）加深學生對長方形和正方形特征的認識，通過探究菜地分割的數學問題，明確格子數與形狀的聯系，從而促進學生空間觀念的發展。

（2）在嘗試、推理、概括等活動中，引導學生深入理解并準確運用游戲規則，形成有序且全面的思考方式，提高他們排除錯誤假設和進行邏輯推理的能力。

（3）通過師生互動和交流溝通，促進學生在數學語言表達和社會交往方面的發展，同時讓學生體驗數學游戲的樂趣。

二、游戲實施過程

（一）在操作辨析中掌握游戲規則

游戲規則是構成游戲的精髓，學生在參與游戲之前要先理解并熟練掌握這些規則，這樣才能在游戲中準確判斷自己和其他玩家是否遵守規則，并且有效地迎接游戲挑戰。對于二年級學生而言，他們主要依賴具體形象思維，因此在理解游戲規則中復雜的文字描述時可能會遇到障礙，一次性理解所有規則對他們來說也頗具挑戰。鑒于此，教師在游戲規則理解階段采用了分段法和辨析法兩種策略。通過兩個階段的具體操作和演示，逐步分解難點；接著通過正例和反例的辨析，迅速將游戲規則聚焦于數量和形狀這兩個關鍵維度，幫助學生掌握游戲的核心要素。

【教學環節1】創設情境，理解規則

1.初步了解游戲規則

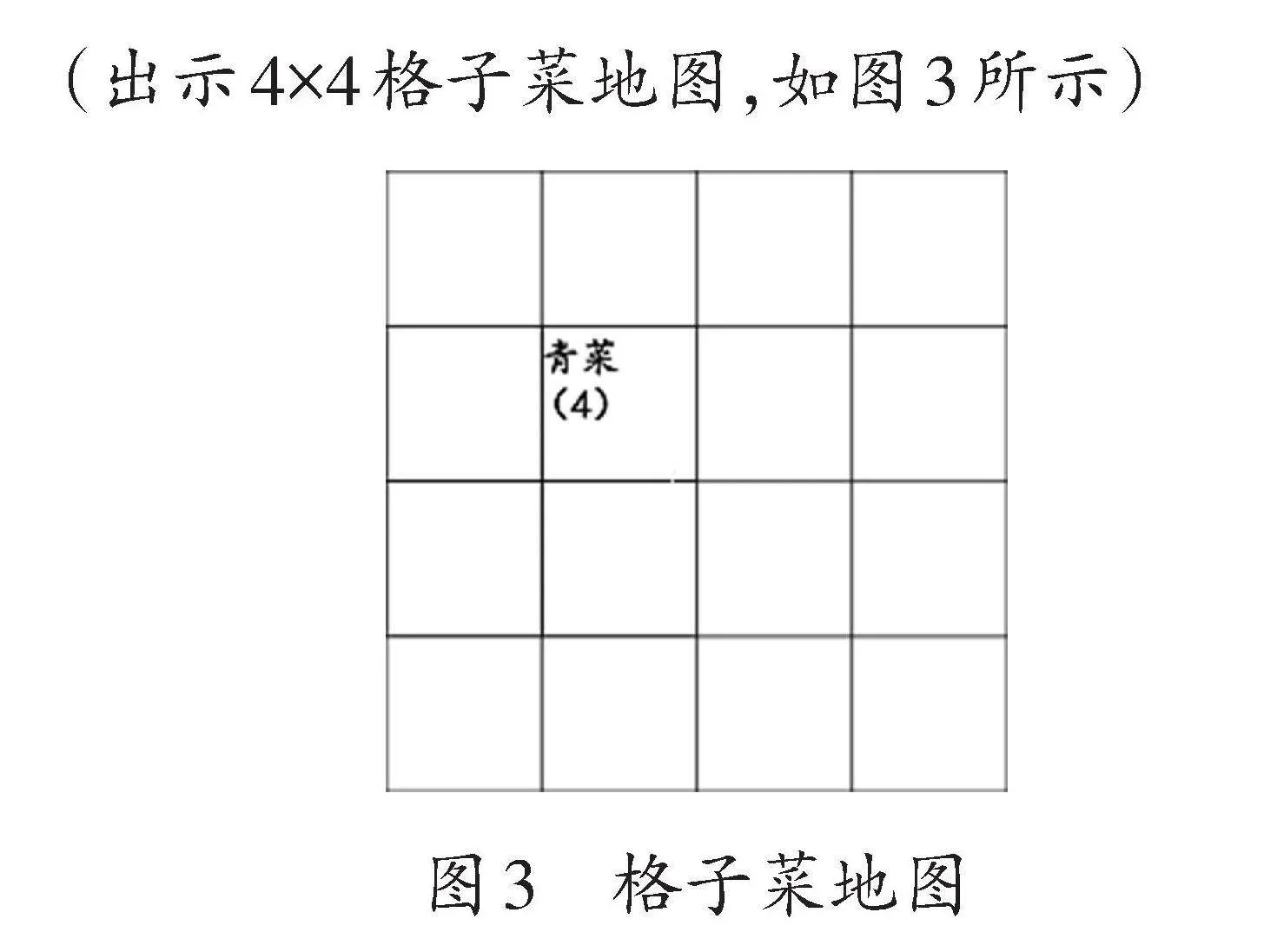
（出示4×4格子菜地圖，如圖3所示）

師：兔媽媽將格子菜地分割成長方形或者正方形，準備種植一些蔬菜。其中一塊地種植的是青菜，你知道青菜一共種植了幾格嗎？

生：菜地上寫著“青菜（4）”，應該要種植4格。

師：學習數學就要有這樣敏銳的眼光。再看看這4格青菜地還有什么特別的要求？

生：形狀必須是長方形或正方形。

師（小結）：在觀察格子菜地時，不僅要關注種植的格子數量，還要考慮菜地的形狀。

2.逐步明晰游戲規則

師：4格青菜可以怎么種呢？請畫一畫。

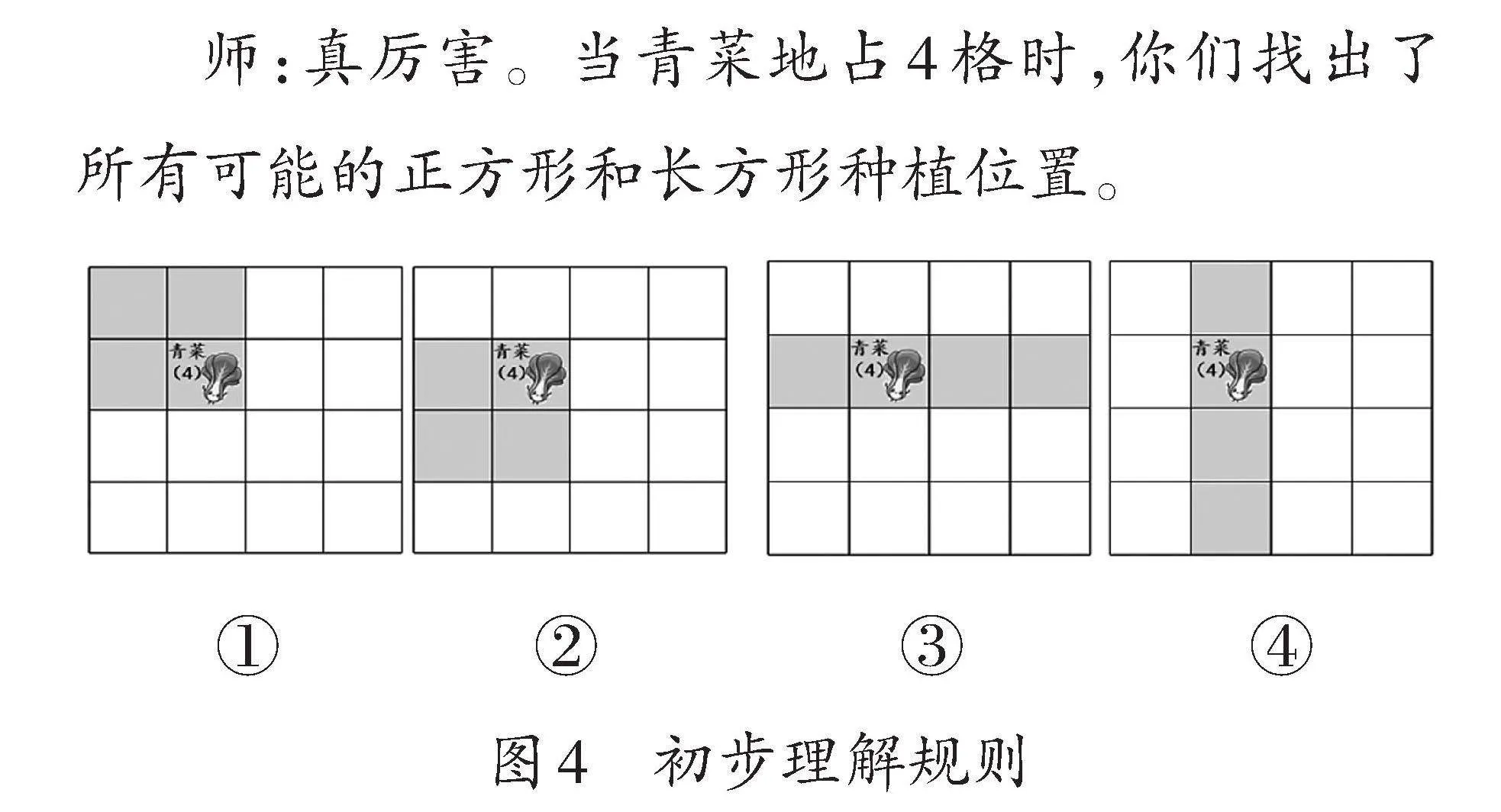
生：我的青菜地是正方形，正好是占4個格子（如圖4-①）。

生：我的青菜地也是正方形，不過位置有所不同（如圖4-②）。

生：我也發現了不同的青菜種植位置，從左上角開始畫，共畫出了四種情況。

師：除了正方形之外，青菜還可以種在什么形狀的菜地上呢？

生：還可以是長方形，一行4格或者一列4格（如圖4-③④）。

師：真厲害。當青菜地占4格時，你們找出了所有可能的正方形和長方形種植位置。

師：小兔子還打算在菜地上種植土豆。土豆地要占3格，應該怎么種植呢？

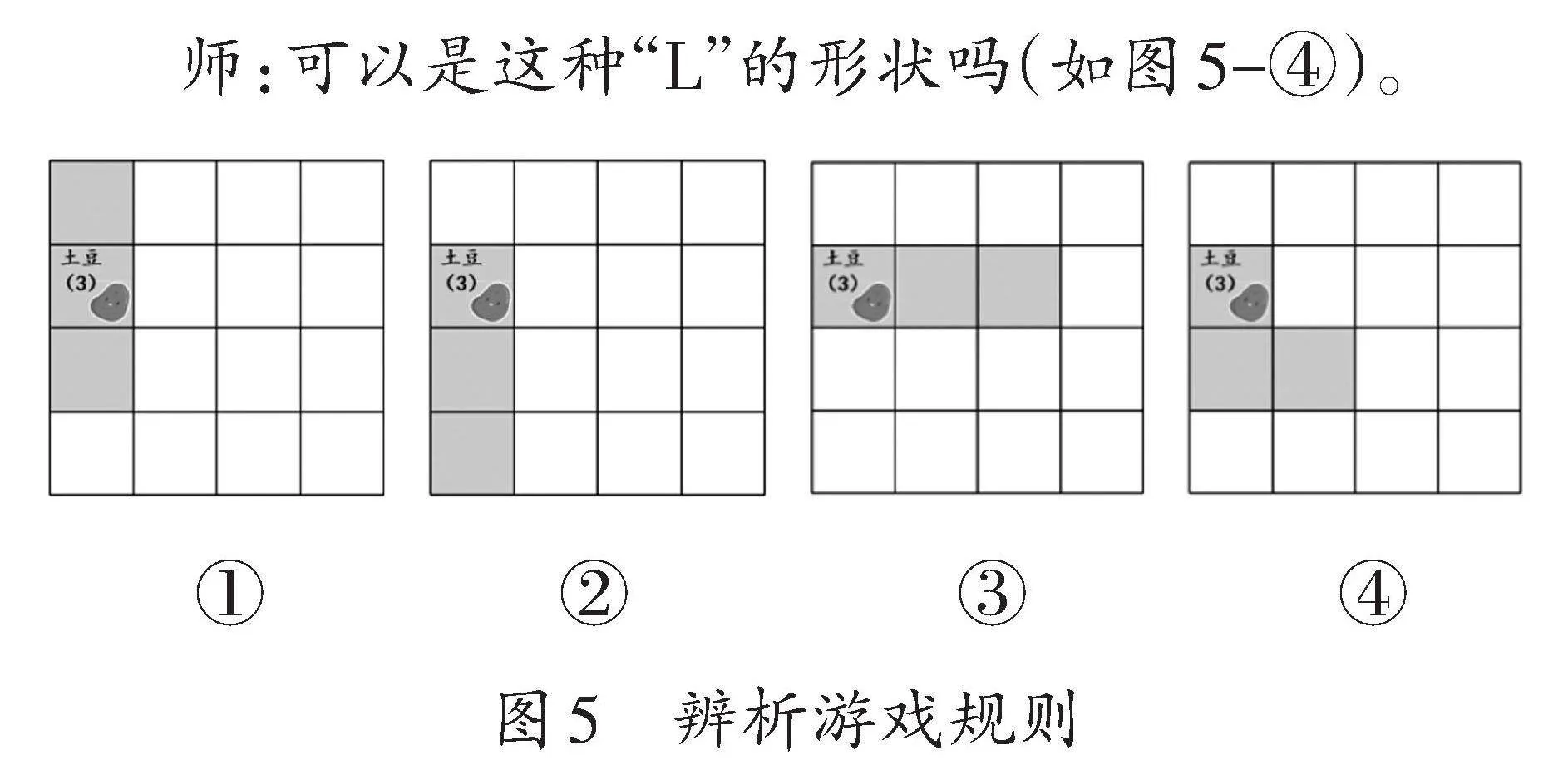
生：可能是3格一行或者3格一列（如圖5-①②③）。

師：可以是這種“L”的形狀嗎（如圖5-④）。

生：L的形狀既不是長方形也不是正方形，3格的菜地不可能是正方形，只能是長方形，要么在同一行，要么在同一列，否則就不符合游戲規則。

師（小結）：在關注菜地形狀與數量的同時，還需要有序地進行思考，這樣才能使菜地形狀的排列具有更多的可能性。

在本教學環節中，教師通過提供一個格子數來尋找長方形、正方形的數學活動，讓學生在理解規則的過程中進一步明確圖形特征。教師通過格子數讓學生想象構建不同的圖形，并引導學生有序列舉，為游戲挑戰提供了更多可能性。

（二）在嘗試調整中感悟游戲策略

在理解游戲規則之后，教師設計了圖2中的挑戰任務一，讓學生在整塊菜地上根據格子數大小和位置進行分割，引導他們思考最優解法，如尋找突破口、使用符號記錄等方法。教師應重視學生思考的邏輯表達和數學活動經驗的積累，引導學生逐步感悟并歸納游戲策略。

【教學環節2】初次嘗試，感悟策略

（教師出示圖2中的挑戰任務一：4×3的格子菜地）

1.獨立嘗試，不斷調整

師：小朋友們已經知道了格子菜地的秘密，現在讓我們來挑戰第一關。請按照格子菜地的數字把這塊地種滿，要求每位小朋友用對應的四種顏色的水彩筆畫一畫。學習單上提供了很多幅格子菜地圖，如果涂錯了，可以嘗試涂第二幅圖、第三幅圖……

2.整體反饋，感悟方法

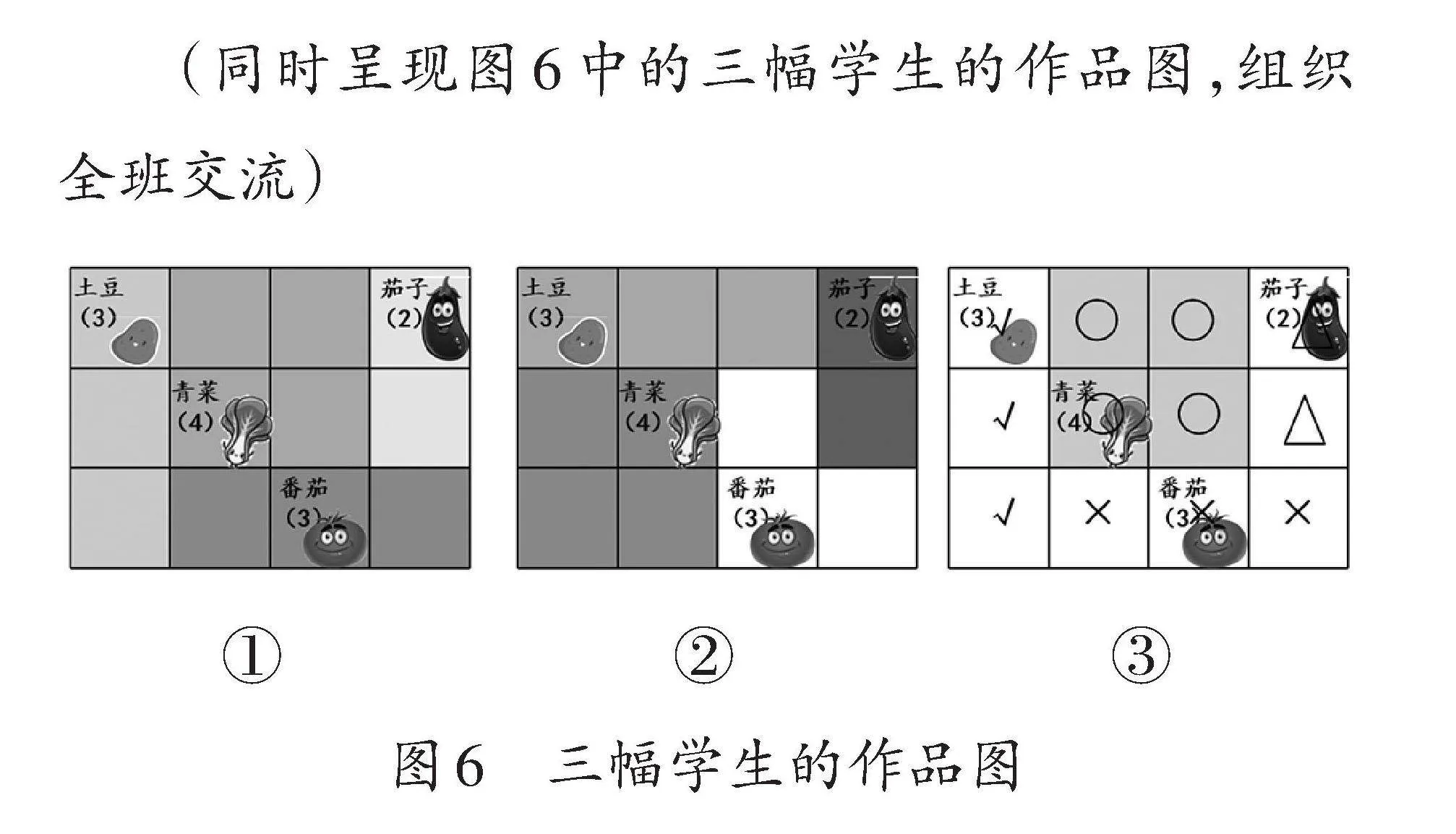
（同時呈現圖6中的三幅學生的作品圖，組織全班交流）

師：對于這三個同學畫出的結果，你們有什么想說的？

（反饋一：學生作品圖6-①）

師：他挑戰成功了嗎？我們怎么來驗證呢？

生：成功了！土豆3格，青菜4格，茄子2格，番茄3格，四種蔬菜地的形狀都是長方形或正方形。而且格子菜地里種滿了蔬菜。

（反饋二：學生作品圖6-②）

師：對于作品圖6-②，你們有什么想說的？

生：先涂土豆、青菜、茄子，剩下的3格不是一個長方形，這種方法不對，這次挑戰失敗了。需要重新畫。

生：我第一次也失敗了，第二次涂圖時，我把土豆地的位置換了一下，就成功了。

師：嘗試時發現錯誤，就要重新調整再挑戰。我們學習數學就需要這種勇于試錯的精神。

（反饋三：學生作品圖6-③）

師：這個小朋友畫了一些符號，你們能看明白嗎？

生：他用“√”“○”“△”“×”表示各種蔬菜地，這樣如果出錯，可以重新調整，找到正確的菜地。

師：這個小朋友真聰明。一邊思考一邊調整，這樣的學習方法值得全班同學學習。

師（小結）：有的小朋友第一次嘗試就成功了，有的小朋友用“嘗試—調整”的方法，經過幾次嘗試也能種好。失敗了不氣餒，值得表揚！

這個教學環節從最簡單的4×3格子圖開始，是游戲的嘗試階段，難度較低，學生能快速獲勝并體驗成功的喜悅。教師鼓勵學生在學習單上記錄每次嘗試的結果，在反饋交流中關注學生嘗試過程中的成功和失敗經驗。通過互動交流，幫助學生回顧哪些做法容易成功，為什么有時幾次嘗試都會失敗，有沒有更好的方法……學生通過不斷辨析，逐步歸納游戲取勝的策略。

（三）在進階活動中發展推理意識

教師可將策略運用與闖關活動相結合，通過設置多層階的進階任務，引導學生從無目的的嘗試轉變為有策略、有目標的挑戰，讓學生在完成這些任務的過程中，發展推理意識。

【教學環節3】方法優化，拓展提升

1.挑戰4×4的格子菜地

（出示圖2中的挑戰任務二：4×4的格子菜地）

師：如何才能又對又快地完成這塊格子菜地的涂色任務呢？

生：先涂4格的青菜地。它不能涂成正方形，也不能涂成豎著的長方形，否則會出現重疊。那只能涂成橫著的長方形，這是唯一的形狀。

師：真厲害。通過觀察，我們找到了青菜地這個突破口，這樣就縮小了選擇范圍。

生：接下來，我們可以確定茄子地的位置，它不能橫著涂，只能豎著向下分割。

生：我們也可以確定土豆地的位置，橫著豎著分割都不行，只能在右下角劃分出正方形。

師：沒錯，在游戲過程中，我們需要先明確哪些可以確定的因素，再不斷嘗試、不斷調整，找到突破口，解決問題。

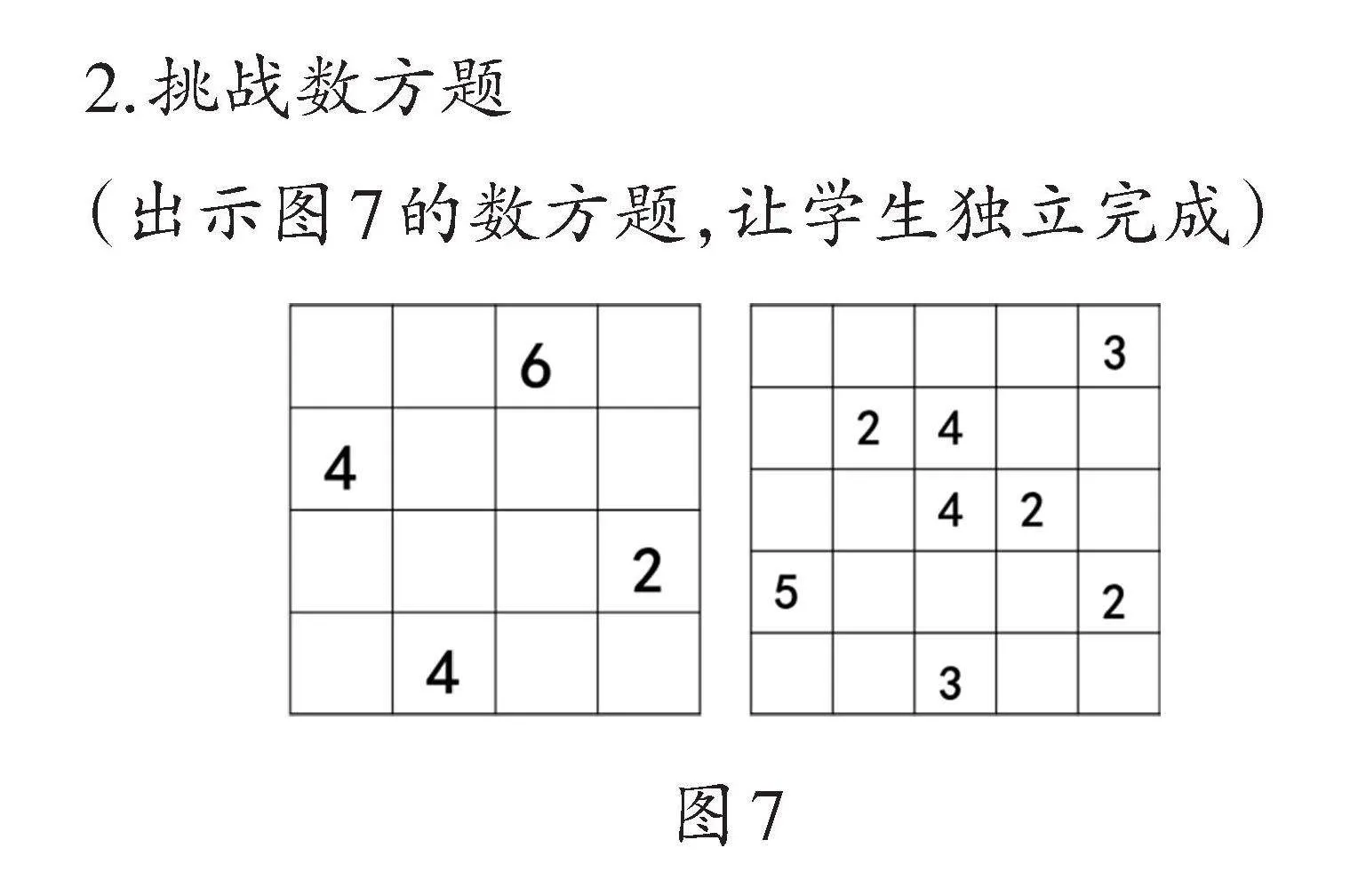
2.挑戰數方題

（出示圖7的數方題，讓學生獨立完成）

師：看看第三關的挑戰，與前兩關有什么不同之處？

生：菜地里的格子數量增加了許多，而且只給出了數字，其中還包括較大的數字5和6。

師：兔子媽媽的菜園不限制種植蔬菜種類，只告訴我們數字保持不變，形狀還是長方形或正方形。請使用不同的顏色來表示數字所代表的格子數量。

師（小結）：我們需要不斷地思考，不斷地嘗試，還要運用一定的策略。

這個教學環節屬于熟練掌握規則并深入游戲的階段。在這個階段中，學生從具體情境過渡到抽象的數方概念，從無策略的嘗試轉變為有策略的推理。特別是當格子數量增加到6時，難度大大提升，不僅考驗了學生的推理能力，還考量了他們的空間想象力。

總之，游戲因其娛樂性和大眾化的特性，與數學的抽象性和邏輯性形成鮮明對比。數學游戲恰好能夠將兩者巧妙地結合起來，既保留了游戲的趣味性，又融入了數學的學科性。在數學游戲課中，教師應將游戲元素與數學相結合，通過創設問題情境，設置游戲進階升級關卡，引導學生主動參與游戲，經歷思考過程，積累活動經驗，發展數學思維。

參考文獻：

［1］張優幼.數學有意思［M］.杭州：浙江教育出版社，2019.

［2］張優幼.基于深度思維的數學游戲規則創編［J］.教學與管理，2019（11）：53-55.

［3］王曉蕾，尚建麗.感悟數學思想 發展核心素養：“數學游戲：漢諾塔”教學實錄與評析［J］.小學數學教育，2022（23）：51-53.

（浙江省臺州市椒江區中山小學楊司校區）