2023年新高考全國Ⅱ卷第22題探究

題目

（1）證明：當0<x<1時，x－x2<sin x<x；

（2）已知函數f（x）=cos ax－ln（1－x2），若x=0是f（x）的極大值點，求a的取值范圍.

1 試題目標

命題考查點：利用導數證明不等式，已知極值點求參數范圍，與三角函數相關的導數.

思想方法：函數與方程思想、數形結合思想、分類與整合思想、化歸與轉化思想.

能力要求：抽象概括、推理論證.

2 試題來源

本題第（1）問源于新教材選擇性必修第二冊第97頁練習的第1題：

利用函數的單調性，證明下列不等式，并通過函數圖象直觀驗證：sin x<x，x∈（0，π）.

此不等式非常重要，建議學生積累不等式鏈“sin x<x<tan x，x∈0，π2”，會證明該不等式，并能應用該不等式進行簡單放縮.

3 試題分析

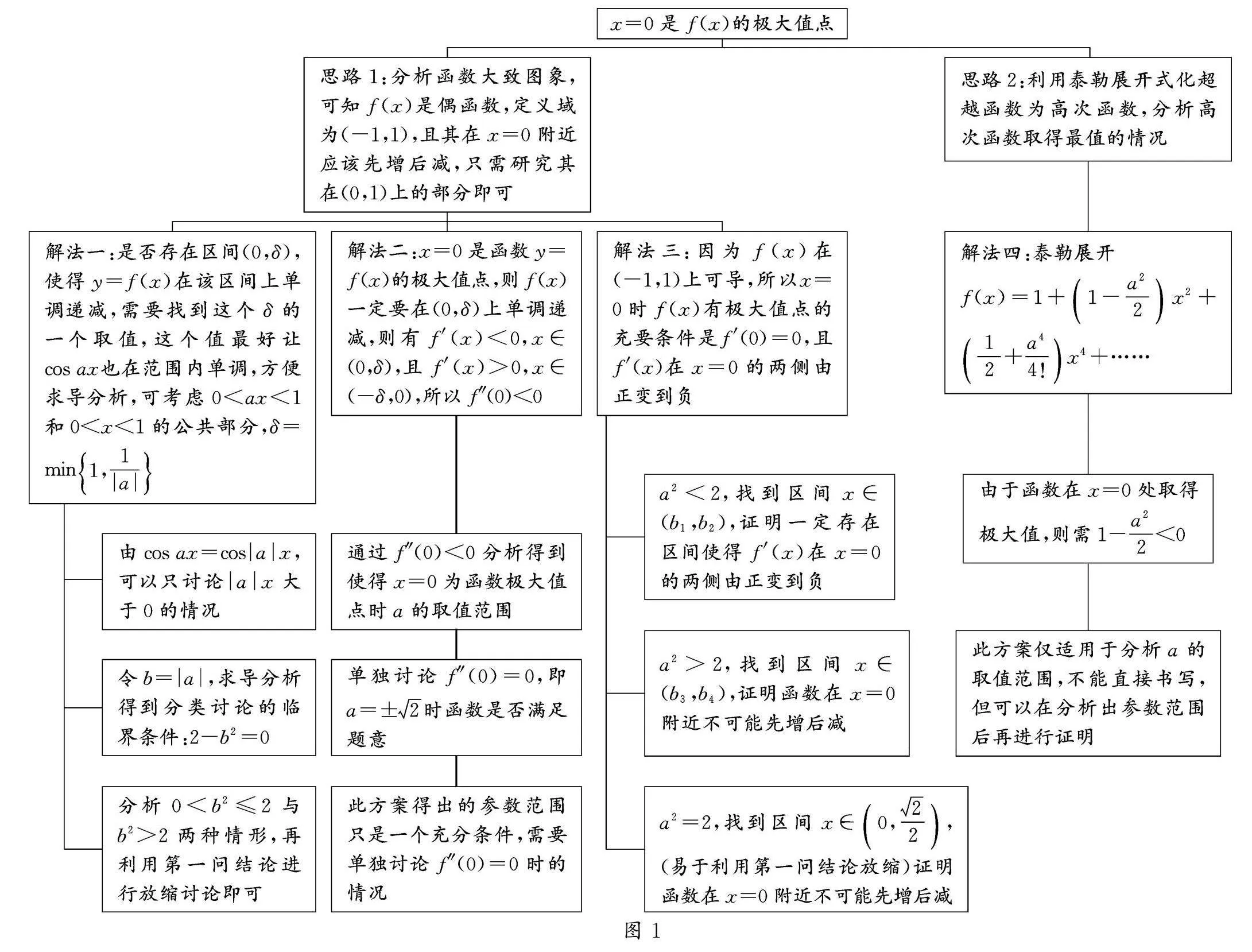
本題的思維導圖如圖1所示.

x=0是f（x）的極大值點

思路1：分析函數大致圖象，可知f（x）是偶函數，定義域為（-1，1），且其在x=0附近應該先增后減，只需研究其在（0，1）上的部分即可

思路2：利用泰勒展開式化超越函數為高次函數，分析高次函數取得最值的情況

解法一：是否存在區間（0，δ），使得y=f（x）在該區間上單調遞減，需要找到這個δ的一個取值，這個值最好讓cos ax也在范圍內單調，方便求導分析，可考慮0＜ax＜1和0＜x＜1的公共部分，δ=min1，1|a|

解法二：x=0是函數y=f（x）的極大值點，則f（x）一定要在（0，δ）上單調遞減，則有f′（x）＜0，x∈（0，δ），且f′（x）＞0，x∈（-δ，0），所以f″（0）＜0

解法三：因為f（x）在（-1，1）上可導，所以x=0時f（x）有極大值點的充要條件是f′（0）=0，且f′（x）在x=0的兩側由正變到負

解法四：泰勒展開

f（x）=1+1-a22x2+12+a44！x4+……

由cos ax=cos|a|x，可以只討論|a|x大于0的情況

通過f″（0）＜0分析得到使得x=0為函數極大值點時a的取值范圍

a2＜2，找到區間x∈（b1，b2），證明一定存在區間使得f′（x）在x=0的兩側由正變到負

由于函數在x=0處取得極大值，則需1-a22＜0

令b=|a|，求導分析得到分類討論的臨界條件：2-b2=0

單獨討論f″（0）=0，即a=±2時函數是否滿足題意

a2＞2，找到區間x∈（b3，b4），證明函數在x=0附近不可能先增后減

此方案僅適用于分析a的取值范圍，不能直接書寫，但可以在分析出參數范圍后再進行證明

分析0＜b2≤2與b2＞2兩種情形，再利用第一問結論進行放縮討論即可

此方案得出的參數范圍只是一個充分條件，需要單獨討論f″（0）=0時的情況

a2=2，找到區間x∈0，22，（易于利用第一問結論放縮）證明函數在x=0附近不可能先增后減

4 解題過程

（1）解析：構建F（x）=x－sin x，x∈（0，1），則F′（x）=1－cos x>0對x∈（0，1）恒成立，則F（x）在（0，1）上單調遞增，可得F（x）>F（0）=0，所以可得x>sin x，x∈（0，1）.

構建G（x）=sin x－（x－x2）=x2－x+sin x，x∈（0，1），則G′（x）=2x－1+cos x，x∈（0，1）.

構建g（x）=G′（x），x∈（0，1），則g′（x）=2－sin x>0對x∈（0，1）恒成立，于是g（x）在（0，1）上單調遞增，得g（x）>g（0）=0，即G′（x）>0對x∈（0，1）恒成立.于是G（x）在（0，1）上單調遞增，可得G（x）>G（0）=0，所以sin x>x－x2，x∈（0，1）.

綜上所述：x－x2<sin x<x.

（2）解法一：常規解法.

根據題意結合偶函數的性質可知，只需要研究f（x）在（0，1）上的單調性，求導，分類討論0<a2<2和a2≥2，結合（1）中的結論放縮，根據極大值的定義分析求解.令1－x2>0，得－1<x<1，即函數f（x）的定義域為（－1，1）.若a=0，則f（x）=1－ln（1－x2），x∈（－1，1）.因為y=－ln u在定義域內單調遞減，u=1－x2在（－1，0）上單調遞增，在（0，1）上單調遞減，則f（x）=1－ln（1－x2）在（－1，0）上單調遞減，在（0，1）上單調遞增，所以x=0是f（x）的極小值點，不合題意.故a≠0.

當a≠0時，令b=|a|>0，可以縮小討論范圍，且方便利用第（1）問結論進行放縮.

因為f（x）=cos ax－ln（1－x2）=cos（|a|x）－ln（1－x2）=cos bx－ln（1－x2），且

f（－x）=cos（－bx）－ln ［1－（－x）2］=cos bx－ln（1－x2）=f（x）.

所以函數f（x）在定義域內為偶函數，換元后函數仍是偶函數，此處給出簡單證明.

由題意，可得f′（x）=－bsin bx－2xx2－1，x∈（－1，1）.

由f′（x）=－bsin bx－2xx2－1>－b2x－2xx2－1=x（b2x2+2－b2）1－x2，發現2－b2≥0時導函數恒大于零，所以可以以此為分析依據對參數進行討論，之后就順理成章了.

（ⅰ）當0<b2≤2時，取m=min1b，1，x∈（0，m），則bx∈（0，1），由（1）可得f′（x）=－bsin bx－2xx2－1>－b2x－2xx2－1=x（b2x2+2－b2）1－x2.

又b2x2>0，2－b2≥0，1－x2>0，所以f′（x）>x（b2x2+2－b2）1－x2>0，即當x∈（0，m）（0，1）時，f′（x）>0，則f（x）在（0，m）上單調遞增.結合偶函數的對稱性可知，f（x）在（－m，0）上單調遞減.故x=0是f（x）的極小值點，不合題意.

（ⅱ）當b2>2時，取x∈0，1b（0，1），則bx∈（0，1）.

結合（1），可得f′（x）=－bsin bx－2xx2－1<－b（bx－b2x2）－2xx2－1=x1－x2（－b3x3+b2x2+b3x+2－b2）.

構建h（x）=－b3x3+b2x2+b3x+2－b2，x∈0，1b，則有h′（x）=－3b3x2+2b2x+b3，x∈0，1b，且h′（0）=b3>0，h′1b=b3－b>0，可知h′（x）>0對x∈0，1b恒成立，所以h（x）在0，1b上單調遞增.又h（0）=2－b2<0，h1b=2>0，所以h（x）在0，1b內存在唯一的零點n∈0，1b.當x∈（0，n）時，則h（x）<0，且x>0，1－x2>0，則f′（x）<x1－x2（－b3x3+b2x2+b3x+2－b2）<0，即當x∈（0，n）（0，1）時，f′（x）<0，則f（x）在（0，n）上單調遞減.結合偶函數的對稱性可知，f（x）在（－n，0）上單調遞增.所以x=0是f（x）的極大值點，符合題意.

綜上，當b2>2，即a2>2，亦即a>2或a<－2時，符合題意.

故a的取值范圍為（－∞，－2）∪（2，+∞）.

解法二：極值的第二充分條件.

由f′（x）=－asin ax+11－x－11+x，

f″（x）=－a2cos ax+1（1－x）2+1（1+x）2，

可得f′（0）=0，f″（0）=－a2+2.所以當a2<2時，f″（0）>0，此時x=0不是f（x）的極大值點；當a2>2，即a>2或a<－2時，f″（0）<0，此時x=0是f（x）的極大值點.這里令f″（0）=－a2+2<0，解出參數的范圍，此僅為充分條件，仍需討論f″（0）=0時的參數取值是否成立.

若a=±2，則f′（x）=－2sin 2x+2x1－x2.當0<x<22時，f′（x）>－2·2x+2x=0，注意到f′（x）是奇函數，所以－22<x<0時f′（x）<0.所以a=±2時，x=0是f（x）的極小值點.

此處利用第（1）問的結論“x>sin x，x∈（0，1）”進行放縮，容易發現不合題意.

綜上，a的取值范圍為（－∞，－2）∪（2，+∞）.

極值的第二充分條件：若x0∈［a，b］，f′（x0）=0，且f″（x0）≠0，則f″（x0）<0時，y=f（x）在x0處取得極大值，f″（x0）>0時，y=f（x）在x0處取得極小值.

證明：

若f″（x0）<0，則有

limx→x0f′（x）－f′（x0）x－x0=limx→x0f′（x）x－x0<0，

即δ>0，當x∈（x0－δ，x0+δ）時，f′（x）x－x0<0.

因此當x<x0時，f′（x）>0，當x>x0時，f′（x）<0.

故f（x）在x=x0取得極大值.

同理可證f″（x0）>0的情形.證畢.

解法三：分析導函數在極值點兩側的正負變化情況.

因為f（x）在（－1，1）上可導，所以x=0是f（x）有極大值點的充要條件是f′（0）=0，且f′（x）在x=0的兩側由正變到負.由f′（x）=－asin ax+11－x－11+x，f″（x）=－a2cos ax+1（1－x）2+1（1+x）2，

可得f′（0）=0，f″（0）=－a2+2.

當a2<2時，f″（0）>0，所以存在區間（b1，b2）（－1，1）（b1<0<b2），有f″（x）>0，x∈（b1，b2）.

所以在區間（b1，b2）上f′（x）單調遞增.又因為f′（0）=0，所以f′（x）在（b1，b2）上由負變到正，故a2<2不符合題意.

當a2>2時，f″（0）<0，所以存在區間（b3，b4）（－1，1）（b3<0<b4），有f″（x）<0，x∈（b3，b4）.

所以在區間（b3，b4）上f′（x）單調遞減.又因為f′（0）=0，所以f′（x）在（b3，b4）上由正變到負，故a2>2滿足題意.

當a2=2時，取區間D=0，22（0，1），由第（1）問可知，當x∈D時，sin2x<2x，所以－2×sin2x>－2x，故f′（x）>－2x+2x1－x2=2x31－x2>0，x∈D，即f′（x）在x=0的右側為正，不符合題意，所以a2=2不符合題意.

綜上，a的取值范圍為（－∞，－2）∪（2，+∞）.

解法四：泰勒展開式.

由泰勒展開式，可得

cos ax=1－（ax）22！+（ax）44！-……，

ln（1－x2）=－x2－x42+……，

則f（x）=cos ax－ln（1－x2）=1+1－a22x2+12+a44！x4+…….由于x=0為極大值且f（0）=1，則需1－a22<0，解得a<－2或a>2.

泰勒展開式在局部分析時功效顯著，而極值恰好就是一個局部特征.

此方案僅適用于分析a的取值范圍，不能直接書寫，可以用此方法推斷出參數范圍后再進行證明.

若學生具備凹凸函數、泰勒展開式等高等數學的知識，解答此類題目會較為容易.這也給我們今后的中學數學教學帶來了一些啟示，教學中可以適當補充一些《數學分析》的知識，以應對難度日益增加的高考.

5 試題拓展

（Ⅰ）（2018全國卷Ⅲ第21題）已知函數f（x）=（2+x+ax2）ln（1+x）-2x.

（1）若a=0，證明：當-1＜x＜0時，f（x）＜0；當x＞0時，f（x）＞0.

（2）若x=0是f（x）的極大值點，求a.

分析：本題兩問都可以用常規解法解答.對于第（1）問，

求導，利用函數單調性證明即可；對于第（2）問，

分a≥0和a<0進行討論，構造函數h（x）=f（x）2+x+ax2，討論h（x）的性質即可得到a的范圍.其中第（2）問還可以利用極值的第三充分條件和泰勒展開求解.

（Ⅱ）（2021年乙卷第10題）

設a≠0，若x=a為函數f（x）=a（x－a）2（x－b）的極大值點，則（）.

A.a<b

B.a>b

C.ab<a2

D.ab>a2

6 試題價值

新課程標準中對導數在函數中的應用提出的要求是：“借助函數圖象，了解函數在某點取得極值的必要條件和充分條件.”本題深入貫徹了課標要求，考查了極值點的充分條件，此部分的內容新教材涉及不多，且解答此類問題需要部分高等數學知識，這也提醒了教師在之后的教學中需要滲透部分必要的高等數學思想，利用這些思想可以幫助我們解出題目中要求的參數范圍，進而再用高中數學的基本方法證明此范圍的充要性，這也對今后學生的數學抽象和邏輯推理核心素養提出了更高的要求.