情境創設，概念教學

摘要：概念教學是高中數學教學中一個非常重要的環節，也是充分展示教師能力水平與教學經驗的場所，設計契合教學規律，落實核心素養，適合學生思維習慣，引起學生共振的教學設計是教師不斷追求的目標.結合三角函數的概念教學，合理創設情境，巧妙設置問題，優化教學過程，完善教學設計，做了一個很好的嘗試.

關鍵詞：三角函數；概念；正弦；余弦；正切；教學設計

1 教材分析

三角函數是在學習了函數的基本概念，以及冪函數、指數函數、對數函數等基本初等函數的基礎上加以學習的，延續了初中的銳角三角函數定義，在此基礎上結合任意角的推廣加以深入學習.作為函數主線的一個延續，三角函數是高中階段學習的最后一個基本初等函數.同時，三角函數又與前面學過的其他基本初等函數有一些差別，特別是三角函數是合理描繪客觀世界中周期性變化規律的一類重要函數模型，在數學學習與其他領域中有著非常重要的作用.

本節課基于銳角三角函數定義以及“任意角和弧度制”，結合角的推廣與三角函數的引入來構建本知識模塊.借助現實世界中的周期性現象與特殊模型，深刻感受三角函數概念的必要性，并借助單位圓的引入與直觀作用來定義相應的正弦函數或余弦函數.

2 教學分析

2.1 學習目標

（1）會通過求任意角的終邊與單位圓交點的坐標來求任意角的三角函數值.

（2）能理解任意角的三角函數的定義，以及定義產生的背景與實際應用，并在此基礎上掌握相應三角函數的定義；進一步加深對函數的概念、表示等的理解與掌握.

2.2 學科素養目標

（1）通過數形結合探究三角函數的概念，培養直觀想象與數學抽象素養.

（2）通過對實際生活案例的探究，利用三角函數構建模型，培養數學建模素養，提高數學能力.

2.3 重點與難點

（1）教學重點：理解任意角三角函數的定義，能利用定義求任意角的三角函數值.

（2）教學難點：理解三角函數是刻畫現實世界中具有周期性變化現象的數學模型，能從現實生活實例中抽象出三角函數模型并解決實際問題.

3 教學過程

3.1 復習回顧，創設情境

（1）課前回顧

問題1前面部分，我們已經學習了任意角和弧度制的相關知識.請完成對應的概念填空（學案內容，這里略）.

師生活動：學生課前預習，自主完成.教師直接提問，檢查學生完成情況.

教學說明：復習任意角與弧度制的定義，為引入三角函數的概念奠定基礎；通過表格的填寫，一是檢驗之前所學知識的掌握情況，二是發現所學知識的局限性，即無法知道超出銳角之外的角的三角函數值，產生認知沖突，為拓展做好鋪墊.

問題2初中只學習了銳角三角函數的概念，現在角的概念拓展到了任意角，三角函數的概念又該如何重新定義呢？

（2）情境探究

探究活動1：筒車（如圖1）是我國古代發明的一種水利灌溉工具，明朝科學家徐光啟在《農政全書》中用圖畫描繪了筒車的工作原理（如圖2）.因其經濟又環保，至今還在農業生產中得到使用.基于理想模型，假定筒車上的每一個盛水筒都進行著勻速圓周運動.

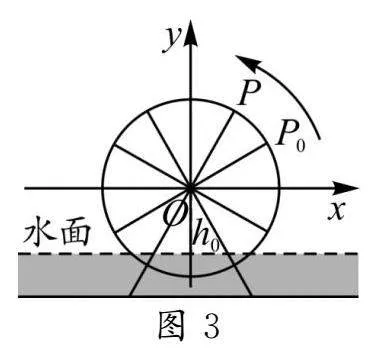
簡單抽象，視盛水筒為一個簡單的質點P，那么點P的運動規律就類似于圓周上動點P的位置變化.我們可以將簡車抽象為一個幾何圖形，建立平面直角坐標系（如圖3）.

教師活動：為方便研究，我們構建出筒車的數學現實模型如下：筒車轉輪的中心點O到水面的距離為h0，其半徑r=1，按逆時針方向勻速轉動，假定轉動一周需要360 s.（針對該問題，這里的角速度是多少？即一秒轉動多少度？）從初始位置點A出發（圓周與x軸正半軸的交點），求經過t s后，點P相對于水面的高度h的表達式.

從圖4來看，給出粗略的表達式（定性刻畫）：h=h0±MP.進一步，結合具體情境，如t=20，40，80時，對應h的表達式分別是怎樣的？

一般地，過了t s呢？猜想：h=h0+sin t°.

師生活動：學生討論后發現，隨著時間的推移，筒車不斷轉動，角度也不知不覺地推廣到了任意角.結合探究過程，請學生討論“對于任意角α，sin α該如何定義才合情合理”？

教學說明：基于問題的探究，合理猜想，并在猜想的基礎上加以合理推理與應用，這也是概念類教學中比較常用的一種基本教學模式，充分體現數學學科的自然性與應用性.

3.2 模型分析，構建新知

探究活動2：對問題進行合理猜想與推測，得出h=h0+sin t°，這里時間為t s.而借助幾何關系h=h0±MP進行比較，則滿足sin t°=±MP.

師生活動：結合圖4加以直觀分析，通過點P→∠POA→MP→sin ∠POA=±MP，形成一個關系鏈.

教師：隨著點P的變化，對應坐標系，可知±MP的絕對值與MP長度相等，其對應的符號在第一或第二象限是正的，在第三或第四象限是負的.

師生活動：歸納可知，可借助點P的縱坐標y來表示并代換相應MP或－MP的值.

教學說明：基于初中銳角三角函數的定義中比值形式，過渡到坐標系中的坐標比值，形成知識的類比與延續，進一步深化初中與高中數學之間的自然過渡與聯系.

探究小結：綜合上述探究過程，總結提煉三角函數的概念.（教材中第178頁內容，這里略.）

我們將正弦函數、余弦函數和正切函數統稱為三角函數.

3.3 實例剖析，鞏固概念

例1（課本第178頁例1）求5π3的正弦、余弦和正切值，并總結方法步驟.

方法步驟：（1）畫出角5π3的終邊，與單位圓交于點B；（2）過點B向坐標軸作垂線，求出點B的坐標；（3）根據定義寫出角5π3的三角函數值.

教學說明：畫出角的終邊，求出其與單位圓交點的坐標.強化關鍵知識的掌握，落實關鍵能力的訓練，同時在學生展示過程中關注解題過程的規范性.

練習1利用單位圓的三角函數定義，請每組同學負責一個角度的三角函數值計算.（題略）

學生活動：分組完成，答案交流.

教學說明：合理有效且及時的鞏固是學習概念、公式等最為有效的方式，結合例題與相應的練習，可以很好達到目的，同時不斷加以強化.

3.4 探索提升，完善成果

探究活動3：已知角θ的終邊過點P（－4，3），求角θ的三角函數值.

教學說明：對課本例2進行取值處理，引導學生從特殊到一般理解方法，同時掌握與任意點坐標相關的計算公式.

探索成果：如圖5，設α是一個任意角，它的終邊與單位圓交于點P（x，y），點P與原點的距離為r=|OP|=x2+y2，則可得sin α=yr，cos α=xr，tan α=yx.

練習2（課本第180頁練習3）已知角θ的終邊過點P（－12，5），求角θ的三角函數值.

教學說明：從不同思維視角確定求解角的三角函數值的技巧與方法，拓展思維，提升應用.

3.5 課堂小結，梳理體系

教師活動：（1）三角函數是刻畫現實世界中具有周期性變化現象的數學模型，例如筒車的盛水筒隨筒車轉動源源不斷運水灌溉這一運動規律.

（2）本節課借助單位圓建立一般三角函數的概念，具體計算步驟為：畫出角θ的終邊，其與單位圓交于點P0；過點P0向坐標軸作垂線，求出點P0的坐標；根據定義寫出角θ的三角函數值.

4 教學反思

4.1 優點剖析，繼承發揚

整個教學案設計清晰規范，各環節設計合理，注重數學知識的生成過程，注重情境引入，課內教學形式多樣，充分發揮了學生自助、互助以及教師幫助的作用，充分調動了學生的學習積極性，學生思維活躍，課內注重必備知識的落實、關鍵能力的培養和核心素養的發展.

4.2 缺點建議，優化提升

在具體設計中，要有機構建初中的銳角三角函數定義與高中的任意角三角函數定義這兩個概念之間的關系，形成一個連續的思維過程與升華過程.同時，在具體教學中，教師要注意指出學生展示中的規范性問題，從細節入手，細致到位.