一節探究拋物線性質“y1y2=-p2”的專題討論課

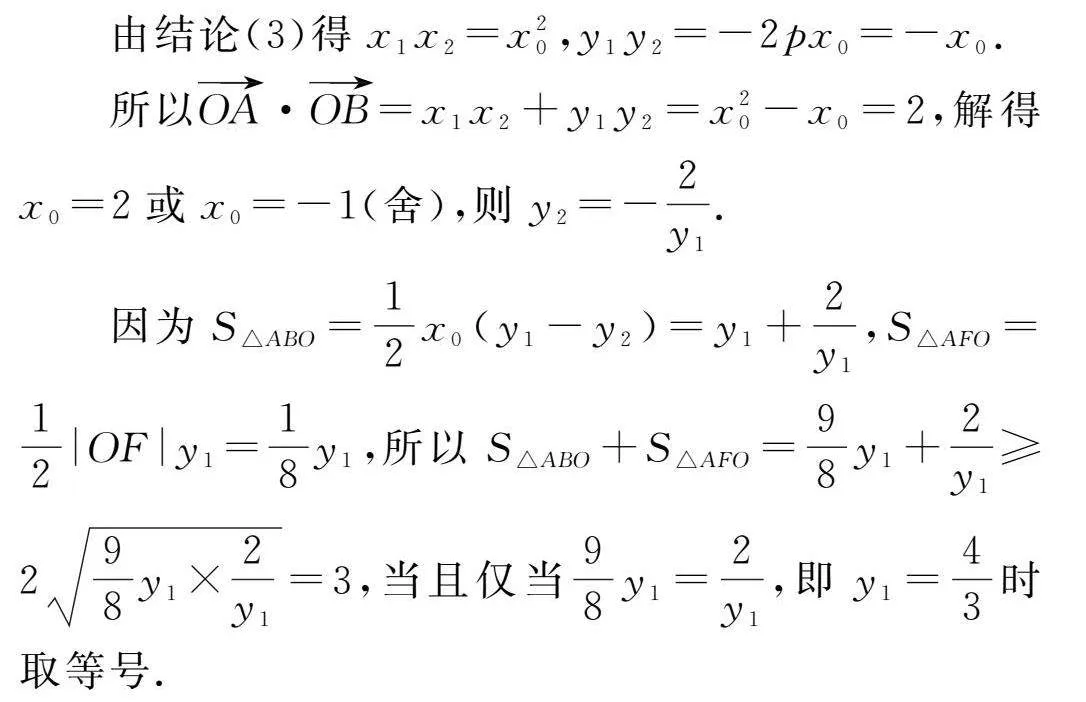
專題討論課是師生在學習過程中以某個教學內容為中心，在教師的指導下，學生先自學，再進行課堂討論的教學模式.高中數學在某些章節內容上完后，可以適當地開展專題討論課.通過這種方式，既可以加深對所學內容的理解，又可以促使學生產生新的想法，開闊眼界和思路，培養他們獨立思考的能力.

1 專題討論課的步驟

專題討論課的開展一般包含以下四步：

（1）教師事先根據學生遇到的問題或難點，和學生共同商定研究主題，并在組長的帶領下提前進行自學和小組研究；

（2）小組確定組員在課堂上分享各小組研究成果，其他學生有不同意見可以進行補充；

（3）教師作為課堂的引導者，必要時解答學生的疑問，并給予細致講解和歸納；

（4）課程結束時，教師要引導學生對問題進行總結提升，并適當給予評價和褒獎.

2 專題討論課案例

在學拋物線性質的過程中，學生對拋物線的性質“y1y2=-p2”產生了濃厚的興趣，要求老師組織一節課開展專題學習，于是筆者和學生一起開展了一次專題討論活動.

2.1 問題的提出

課前，針對這個性質，給學生提出了以下問題：過拋物線y2=2px（p＞0）焦點的一條直線和這條拋物線相交，兩個交點的縱坐標為y1，y2.

（1）要證明y1y2=-p2可以從哪些角度入手，分別怎樣證明？

（2）此性質還可以做哪些引申推廣？能否根據這一性質得到一些新的結論？

（3）由此性質推廣出的結論可解決哪些題型？

2.2 性質證明的探討

針對上述問題（1），大家共同探討，得到證明思路如下：

三組A同學：“由“y1y2=-p2”，聯想到韋達定理中的兩根之積，從而形成解題方向一.

四組B同學：“對于拋物線的焦點弦，常規解決方法是利用拋物線定義進行轉化，形成解題方向二”.

見學生沉默下來，筆者決定適當引導一下：“同學們，直線過焦點，事實上就是直線和拋物線的兩個交點與焦點三點共線，從三點共線的角度又可以形成怎樣的證明方向呢？”

一組C同學積極發表了意見：“老師，可以利用直線方程和直線斜率公式解決.”筆者及時給予肯定：“C同學思維很活躍，還有同學有其他的想法嗎？”

學生想了一會兒，六組D同學補充發言說：“老師，我覺得還可以利用共線向量解決以及定比分點公式解決.”

學生的證明思路越來越廣，于是筆者留了十分鐘讓小組進行討論，并讓幾位學生將他們的證明過程投屏.

證法1：利用韋達定理.

當過焦點的直線斜率不存在時，直線方程為x=p2，代入y2=2px得y=±p，故y1y2=-p2成立.

當直線斜率存在時，設其方程為y=kx-p2（k≠0），則x=yk+p2，代入拋物線方程y2=2px并整理得y2-2pyk-p2=0，由韋達定理知y1y2=-p2.得證.

證法2：利用拋物線定義.

記過焦點F的直線與拋物線交于兩點P1，P2，并設P1y212p，y1，P2y222p，y2.過點P1，P2分別作準線的垂線P1P′1，P2P′2，P′1，P′2

為垂足.由拋物線定義知|P1P2|=|FP1|+|FP2|=|P1P′1|+|P2P′2|，即

y212p-y222p2+（y1-y2）2=y21+y222p+p，

兩邊平方整理得（y1y2+p2）2=0，所以y1y2=-p2.

證法3：利用斜率公式.

記過焦點F的直線與拋物線交于兩點P1，P2，并設P1y212p，y1，P2y222p，y2.

當過焦點的直線斜率不存在時，直線方程為x=p2，代入y2=2px得y=±p，故y1y2=-p2成立.

當直線斜率存在時，

k=y1-y2y212p-y222p=y1y212p-p2，

整理得y1y2=-p2.

證法4：利用三點共線.

由兩點式可得焦點弦P1P2所在的直線方程為

y212p-y222p（y-y1）=（y1-y2）x-y212p，

而焦點Fp2，0在直線上，則有

y212p-y222p（0-y1）=（y1-y2）p2-y212p.

整理，得y1y2=-p2.

證法5：利用共線向量（略）.

證法6：利用定比分點（略）.

筆者不斷引導學生，讓他們從多角度思考問題，并鼓勵學生積極參與探索、思考、創造，由此激發學生的創新意識，培養創新能力.

2.3 性質結論的引申

學生發現一個小小的性質可以有如此多的證明方法特別激動，但不能讓學生因為暫時的收獲興奮不已而阻擋思維的腳步，教師作為引領者要進一步引導學生去探索和發現：“同學們，拋物線的這一性質是否可以推廣和引申呢？”就像剛爬上山頂又遇到一座更美麗、更高的山峰，學生的斗志又被激發出來了.師生共同研究，學生總結了如下新的結論：

結論1若一條直線過拋物線y2=2px（p＞0）

的焦點且與其交于不同的兩點（x1，y1），（x2，y2），則x1x2=p24，y1y2=-p2.

結論2若一條直線與拋物線y2=2px（p＞0）的兩交點坐標為（x1，y2），（x2，y2），且x1x2=p24（或y1y2=-p2），則該直線必過拋物線的焦點.

結論3若拋物線y2=2px（p＞0）上有兩個點分別為A（x1，y1），B（x2，y2），且直線AB與x軸交于M（x0，0），則y1y2=－2px0，x1x2=x20.

結論4若一條直線與拋物線y2=2px（p＞0）交于A（x1，y1），B（x2，y2）兩點，且y1y2=－2px0（或x1x2=x20），則該直線必過點（x0，0）.

2.4 性質結論的應用

在學生得出結論的基礎上，筆者進一步加以引導：“同學們，在遇到問題時大家開動腦筋積極思考探究，這種研究精神太可貴了！給你們點贊！我們進一步探究一下，用你們總結的結論可以解決哪些問題呢？”學生一聽，興致更高了，有的翻書，有的查資料，有的討論，熱火朝天！

過了大概七八分鐘，六組的E同學勇敢地走上了講臺，展示了她設置的題目和她的解答過程.

應用1過拋物線y2=2px（p＞0）焦點F的一條直線與拋物線交于P，Q兩點，設直線OP交準線于點M.

求證：直線MQ平行于拋物線的對稱軸.

證明：設P，Q的坐標分別為y212p，y1，y222p，y2，則

OP所在直線方程為y=2py1x.

令x=-p2，得yM=-p2y1.

又y1y2=-p2，則y2=-p2y1，所以

y2=yM.

故直線MQ平行于x軸，即直線MQ平行于拋物線的對稱軸.

筆者忍不住感嘆：“哇，E同學真是一個細致又樂于思考的好同學，不僅對課本的例題了如指掌，而且可以另辟蹊徑找到不同的解法，分析得非常到位！”筆者這一頓夸獎，使得學生一個個像打了雞血一樣，爭先恐后地要上臺展示.

五組的范同學沖上講臺，展示了他的聰明才智.

應用2已知點A（－1，0），B（1，－1），拋物線C：y2=4x，過點A的動直線l交拋物線C于M，P兩點，求OM·OP的值.

解：設M（x1，y1），P（x2，y2），因為M，P，A三點共線，所以

由結論（3）得x1x2=x2A=1，

y1y2=－2pxA=－2×2×（－1）=4.

所以OM·OP=x1x2+y1y2=5.

這位范同學有點小聰明但是學習持久力不強，剛好借此機會把他狠狠夸了一頓.筆者帶頭鼓起了掌：“小范老師設置的題目太好了，用了推導的新結論，長此以往，怕是要坐上為師的寶座了！”同學們哄堂大笑，使勁兒鼓起了掌！范同學雖然臉紅了，但是腰挺得更直了！

眼看快下課了，筆者說：“還有最后一個機會給你們！”說時遲那時快，沈同學已經把她的勞動成果投屏到黑板上.

應用3已知F為拋物線y2=x的焦點，點A，B在該拋物線上且位于x軸的兩側，若OA·OB=2，求△ABO和△AFO面積之和的最小值.

解：設直線AB與x軸的交點為（x0，0）（x0>0），A（x1，y1），B（x2，y2），y2<0<y1.

由結論（3）得x1x2=x20，y1y2=－2px0=－x0.

所以OA·OB=x1x2+y1y2=x20－x0=2，解得

x0=2或x0=－1（舍），

則y2=－2y1.

因為S△ABO=12x0（y1－y2）=y1+2y1，

S△AFO=12|OF|y1=18y1，所以

S△ABO+S△AFO=98y1+2y1≥298y1×2y1=3，

當且僅當98y1=2y1，即y1=43時取等號.

所以△ABO和△AFO面積之和的最小值為3.

筆者忍不住夸獎：“在如此短的時間內，沈同學設置了如此典型的例題，不僅用到我們得到的結論，還利用了重要不等式求最值！”學生都向她投去了佩服的目光，這是前進過程中最大的動力.此時已快下課，筆者帶領學生簡明扼要地總結了本次活動課，并鼓勵和肯定學生的積極表現.

3 課后思考

通過本次專題討論課，學生掌握了新知識，解決了新問題，深刻體會到創造的喜悅，富有新意，也是創新意識的表現.在教學過程中，教師要對學生的性格了如指掌，對學生的表現及時給予恰當的肯定和鼓勵，哪怕是有些夸張的贊美，也能增強勇于表現的學生的自信心，其他學生看到臺上學生的優異表現，表現欲望也更強烈，從而形成良性循環.

作為一名戰斗在一線的教育工作者，幫助學生打下扎實的知識基礎，形成良好的學習習慣以及探索鉆研的精神，讓他們對數學學習保持極大的持續的熱情，是我們的首要責任.所以，在以后的教學中，還要不斷地探索和思考，為學生的創新精神和實踐能力打下堅實的基礎.