基于波利亞解題理論的實例分析

【摘要】二次函數是初中數學的重要知識點之一,考查了學生的函數思想和抽象思維能力.在二次函數的教學過程中,提高學生關于二次函數問題的解題能力,可以促進他們抽象思維的發展和數學素養的培養.本文將波利亞的解題理念與二次函數教學相結合,將其運用到二次函數問題的解答之中,并列舉實例進行講解,以期提高學生解決二次函數問題的能力.
【關鍵詞】初中數學;波利亞理論;二次函數
1 精細分析條件,擬定合適計劃
在進行二次函數教學時,教師扮演著引導學生、激發解題靈感的角色,幫助學生在題干的已知條件和待求的未知量之間建立聯系.當然,促使學生靈感激發并不是一朝一夕之事,需要學生有豐富的解題經驗和深厚的理論知識.因此,教師在教學過程中,應該不厭其煩地為學生鞏固知識點,并傳授分析問題、解決問題的技巧,引導他們找到明確的解題思路,形成經驗總結.以下題為例.
例1 已知拋物線的解析式為y=x2+bx+c,將其圖象先向上平移2個單位,再向左平移5個單位,最終得到的圖象的解析式為y=x2+4x-5,請問b和c的值是多少?
教師 請認真思考,對于這個問題,大家在解題上有沒有想法分享?
學生1 這個問題考查的是二次函數圖象的平移規律,已知平移后圖象的解析式,以及平移過程,我們可以從“左加右減,上加下減”的角度入手,順向推理,求出原函數平移后的解析式,然后根據系數相等的原則求出b和c的值.
學生2 我同意這個解法,在之前碰到的題目中,題干中都給出了二次函數的具體表達式,以及平移過程,然后要求我們求出平移后的表達式.這個題目雖然原式解析式未知,但是一樣可以用這個方法,我們可以先把原函數看作已知,按照平移規則得到平移后的解析式,然后將系數作等號,求得b和c的值.
教師 非常棒!同學們不僅對這道題的分析非常正確,而且還能聯系到之前遇到過的題目.那么按照剛剛的思路,同學們動手試試看能否解出答案!
……
教師 好,同學們都解完了吧,我們待會兒再核對答案.現在我們再思考一下,這個問題能不能采用逆向思維進行解答.注意,平移后的函數是沒有未知數的.
學生3 可以,題干已給出平移后的函數解析式,將平移過程逆向,可以還原回原函數的表達式,從而求出未知數的值.
教師 舉一反三非常棒!大家試著計算一下,看解得的答案是否一致,另外再看看有沒有新發現.
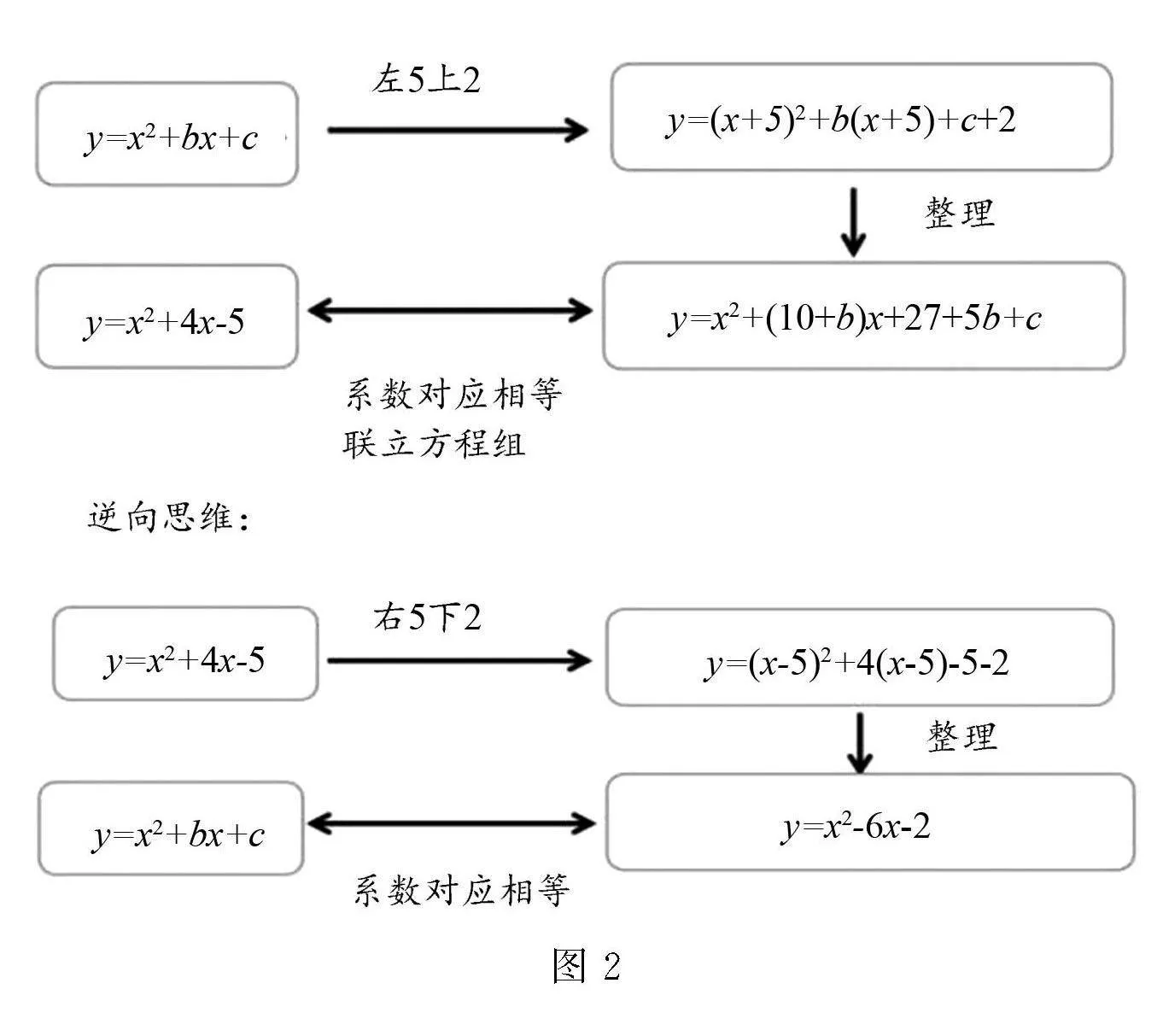
解題分析 解題思路如圖2所示.
圖2
2 鼓勵學生一題多解,發散學生思維
“條條大路通羅馬”,但每條通往羅馬的道路其通暢程度是各有不同的,解答數學問題也是如此.在解答數學問題時,雖然從不同的角度切入或采用不同的方法最終解得的答案是相同的,但運用不同方法涉及的計算量和邏輯推理的難度是不同的.因此,在教學過程中,教師可以多鼓勵、引導學生嘗試用多種解法去解答一個問題,然后分析比較各種方法的優劣之處,找到一個最佳的解題方法.這樣不僅可以讓學生跳出思維定勢,開拓思維,還可以增加該知識點的廣度和深度.以下題為例.
例2 已知點A3,y1,B-1,y2,C2,y3為二次函數y=3x-22+k圖象上的三個點,請判斷y1、y2、y3的大小關系.
解題分析
解法1 代入法
比較3個未知數的大小,最直接的方法是求出它們的具體值,然后進行比較.這里直接使用代入法將A,B,C三點的橫坐標代入解析式中,可得y1=3+k,y2=27+k,y3=k,雖然求出的值中含有參數,但并不影響大小的比較,可直接得到y2>y1>y3.
解法2 對稱軸法
根據題干給出的表達式可知,該函數圖象的開口向上,且對稱軸為x=2,因為C點恰好是圖象的頂點,所以C點的縱坐標最小,即y3最小;又因為A,B兩點位于對稱軸的兩側,我們可以先畫出二次函數的圖象草圖,如圖3所示,從圖象中可以看出,當一個點離對稱軸水平距離越遠時,其縱坐標的值就越大.根據xA=3-2=1,xB=-1-2=3可知,B點距離對稱軸的水平距離更遠,故B點的縱坐標值最大,即y2>y1>y3.
綜上兩種解題方法,可能對于一些基礎較差的學生而言,首先想到的是第一種解法,即代入A,B,C三點的橫坐標進行求值比較.然而,當問題中涉及較多、較復雜的參數時,可能無法對求得的縱坐標進行直接比較,這種方法便不太適用.因此,教師在教學過程中應該多激勵學生去嘗試用多種方法解題,比如對二次函數的圖象特征進行分析,引導他們從另一個角度去發現問題的本質,掌握更多的解題方法,以期望不論在教學還是在解題中都達到舉一反三的效果.
圖3
3 結語
本文對波利亞解題理念在初中數學二次函數問題中的應用進行探究,旨在提高學生解決二次函數相關問題的能力,并為教師提供一個二次函數教學參考.在教學過程中,教師應當作為引導者,引導學生積極思考,想盡辦法讓學生參與到自己的教學過程中,為問題的提出和解決做出自己的貢獻.
參考文獻:
[1]王文艷.基于波利亞解題思想的初中二次函數教學策略研究[D].濟南:山東師范大學,2023.
[2]霍云.思維導圖與波利亞解題思想融合的教學實踐研究——以“二次函數”為例[J].中學數學,2023(18):25-26.
[3]張素元.基于G·波利亞解題理論的二次函數綜合題探析[J].中學數學教學參考,2022(29):42-44.

