大概念引領下的初中數學解題策略與教學創新

【摘要】本文旨在探討大概念引領下初中數學解題策略的創新路徑，通過深入探究教材的核心概念而明確了各概念間的內在邏輯聯系，并以此為基礎構建了多層次的問題探究序列，本文以“探索三角形相似的條件”為例，直觀展示了如何通過追溯概念的核心屬性來引導學生逐步深入探索圖形關系，同時還聚焦核心概念考查而消除了概念間的隔閡與界限，使學生能夠更好地理解數學知識.

【關鍵詞】大概念；初中數學；解題策略

隨著教育改革的不斷深化，初中數學教育正面臨著前所未有的挑戰與機遇，傳統的解題方法、教學模式雖然在過去發揮了巨大的作用，但在新的時代背景下已顯得“力不從心”，因此就需要從“大概念”的角度出發，來重新審視初中數學解題策略與教學創新，以更好地適應時代的需求，以培養出更具創新精神與實踐能力的學生.“大概念”為外來詞語的翻譯，英語表達為“big idea”.從字面解釋上看，“大”區別于“小”，指向學科最本質的部分，也可解釋為上位與高位；“概念”則基于概念本體，即對具體事物本質的抽象［1］.“大概念”引領下的初中數學解題策略是指將數學知識點與實際問題相結合，通過抽象、歸納及演繹等方法找出問題的本質規律，形成具有普遍意義的解題思路，這種策略不僅有助于提高學生的解題能力，更能培養學生的邏輯思維與創新能力.

1 大概念引領下初中數學解題策略創新路徑探析

1.1 深入探究教材核心概念，明確各概念間的內在邏輯聯系

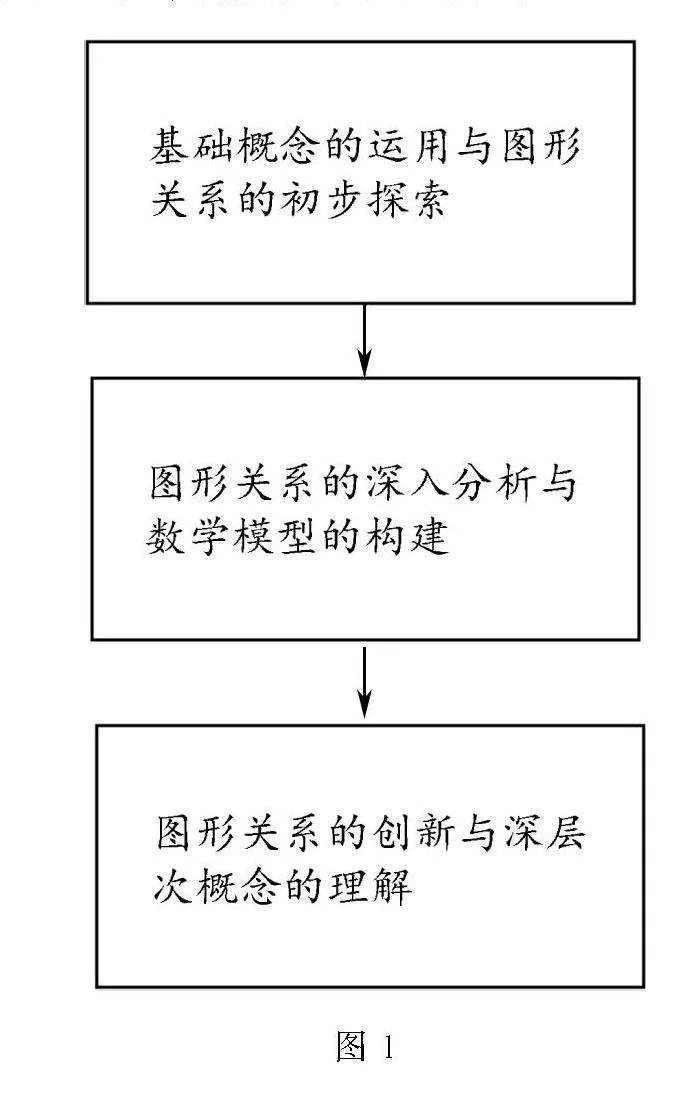
從“探索三角形相似的條件”這一基礎概念出發，我們開始了對圖形關系的初步探索，雖然它并不構成數學學科中的“大概念”，但其揭示了圖形形狀之間的一種本質關系，在九年級下冊的圖形關系學習中，圖形相似作為研究的最后一章，其要求學生能夠清晰地理解與區分多個相關概念之間的邏輯關系.在此之前學生已經學習了三角形、四邊形及圓等基本圖形，并基于此積累了豐富的幾何知識，然而與這些圖形相關的綜合問題也隨著學習的深入而日益增多，這對他們解決綜合問題的能力提出了更高的要求，為了幫助學生更好地理解并應用這些概念，筆者設計了一個“大概念”圖（見圖1）.

圖1

1.2 追溯概念的核心屬性，構建多層次的問題探究序列

問題1 如圖2所示，在矩形ABCD中，AB=2BC，E是AD的中點，F是BC的中點，基于此判斷△ABE與△EBF是否相似并說明理由.

參考答案 首先由于ABCD是矩形，即有∠A=∠B=90°，接著由于E與F分別是AD與BC的中點，而可以得到AE=ED=BF=FC，因此AEBF=EDFC=11，又由∠A=∠B=90°得出∠AEB=∠BFE，再根據“兩邊成比例且夾角相等的兩個三角形相似”而得出△ABE∽△EBF.

追問 在圖2中除了△ABE與△EBF，是否還存在其他的相似三角形？如果存在請表示出來并說明理由.

參考答案 除了△ABE與△EBF相似，還存在△ABE與△EDF相似，因為AB=2BC而E是AD的中點，由此可知AE=ED=BF=FC，因此AEED=BFFC=11，又因為∠A=∠D=90°而得出∠AEB=∠DFE，根據“兩邊成比例且夾角相等的兩個三角形相似”可知△ABE∽△EDF.

圖2

問題2 如圖3所示，在矩形ABCD中，AB=3BC，點E在AD上且AE=2ED，點F在BC上且BF=2FC.

（1）判斷△ABE與△EBF是否相似并說明理由.

（2）若AB=6，求△EBF的面積.

參考答案 （1）由于ABCD是矩形，可知∠A=∠B=90°，又因為AE=2ED且BF=2FC而得出AEBF=EDFC=22=11，據此根據“兩邊成比例且夾角相等的兩個三角形相似”可以得出△ABE∽△EBF.

（2）由于△ABE∽△EBF，根據相似三角形的性質可知EFAB=BFAE，代入已知條件EF6=22解得EF=6，因此△EBF的面積=12×EF×BF=12×6×3=9.

圖3

1.3 概念追問與圖形關系探索

在幾何教學中，通過有層次的概念追問可以幫助學生更深入地理解圖形的內在關系，以下是通過三個不同層次的追問，來引導學生從基礎概念出發并逐步深入探索圖形關系的過程.

追問1 基礎概念的運用與圖形關系的初步探索

在問題1的基礎上通過新增線段豐富了圖形的關系，進一步為學生提供了更廣闊的探索空間，特殊角90°的出現提醒學生要利用直角來證明新的相似三角形，這一追問旨在引導學生關注圖形的位置關系與大小關系，同時注意嘗試運用“兩邊成比例且夾角相等的兩個三角形相似”或“三邊成比例的兩個三角形相似”等基礎知識來解決問題［3］.

追問2 圖形關系的深入分析與數學模型的構建

在追問1的基礎上進一步破壞了正方形邊長相等的關系，但保留了線段的垂直特征，這一變化旨在引導學生思考如何在沒有邊長相等條件的情況下，仍然能夠利用相似的性質得出線段的比例關系，通過這一追問學生可以更加深入地理解相似三角形的性質并學會運用方程來解決實際問題.

1.4 聚焦核心概念考查，消除概念間的隔閡與界限

問題3 如圖4所示，在邊長為6的正方形ABCD中，E是BC的中點，F是AB上的一點且BF=2FA，接著以EF為直徑作⊙O交AD于點G.

（1）求證：△EFG是等腰三角形；

（2）求⊙O的半徑.

參考答案 （1）連接GE，由于E是BC的中點且正方形對角線互相垂直且相等，則可以證明△EBF≌△EAG（ASA）且EF=EG，從而可以證明△EFG是等腰三角形.

（2）由于△EBF≌△EAG，則可知BE=AG=3，在直角△EBF中利用勾股定理可以求出EF=BE2+BF2=9+16=5，得出⊙O的半徑為EF的一半即2.5.

追問1 若F是AB的中點且其他條件不變，求⊙O的半徑.

參考答案 當F是AB的中點時BF=FA=3，在直角△EBF中通過利用勾股定理可以求出EF=BE2+BF2=9+9=32，因此⊙O的半徑為EF的一半即322.

追問2 若E是BC上的一點且BE=2EC，在F是AB的中點且其他條件不變時，求⊙O的半徑.

參考答案 當BE=2EC時E是BC的三等分點，由于F是AB的中點即BF=FA=3，在直角△EBF中利用勾股定理就可以求出EF=BE2+BF2=12+9=21，因此，⊙O的半徑為EF的一半即212.

設計意圖 通過改變點E與F的位置，讓學生體驗在不同情況下如何應用相似與勾股定理來求解圓的半徑，通過追問進一步引導學生深入理解正方形與圓的性質，以此來培養他們的空間想象能力與解決問題的實際能力.

圖4

2 大概念引領下的初中數學解題策略與教學創新梳理

在初中數學教學中首先應立足于教材的原始概念，深入理解并把握各個概念之間的邏輯關系，其中會涉及概念的定義、性質、判定與應用等多個方面，通過厘清這些關系就能夠幫助學生建立起完整的知識體系，進一步為后續的解題與教學創新奠定堅實的基礎.在解題過程中還需注意通過設計多個層次的概念追問，來不斷引導學生逐步深入探索圖形關系，這種追問方式不僅能夠幫助學生鞏固基礎知識，還能夠培養他們的邏輯思維與創新能力，同時通過對圖形的深入分析，學生們也能夠更好地理解概念的本質特征，進一步提高解題的準確性與效率［4］.在解題過程中應始終關注概念的本質特征，避免陷入形式主義的泥潭，通過回歸概念的本質幫助學生更加靈活地運用相關知識來解決問題，還應鼓勵學生構建數學模型，將實際問題抽象為數學問題，來培養他們的數學建模能力與問題解決能力.

3 結語

大概念引領下的初中數學解題策略與教學創新是一個長期而持續的過程，通過立足教材原始概念、設計多層次概念追問、回歸概念本質特征與構建模型以及打通概念壁壘與綜合應用等策略，就可以不斷提高學生的數學素養與創新能力，未來隨著教育改革的不斷深入與新課程標準的實施，我們應繼續探索更為有效的解題策略與教學創新方法，以期能夠為學生的全面發展做出更大的貢獻.

參考文獻：

［1］陳圣文.大概念視角下初中數學微專題教學研究——以函數中幾何圖象變換問題為例［J］.福建教育學院學報，2024，25（02）：49-51.

［2］楊樹峰.初中數學大單元教學的意義、特點和策略［J］.教師教育論壇，2023，36（12）：42-44.

［3］吳超燕.基于大概念的初中美術主題式單元化教學探究［J］.美術教育研究，2023，（16）：176-178.

［4］劉榮玉，王洪凱.大概念視角下初中數學大單元教學設計與策略——以“函數的圖象”為例［J］.現代教育，2023，（07）：19-24.