整合破解策略,思路引導教學


【摘要】與圓有關的陰影部分面積探究教學中,需要解讀中考考查核心,引導學生探索破解策略.整個探究過程建議分為三個階段:階段1,方法講解,模型構建;階段2,實例講解,強化應用;階段3,過程反思,經驗總結.本文針對專題重點進行深入探究,并提出相應的教學建議.
【關鍵詞】圓;面積;構造和差;等積轉化
1 探究綜述
求陰影部分的面積在中考中十分常見,該類問題涉及扇形、弧長、三角形等知識內容,可全面考查學生對圖形的理解,以及數形結合、化歸轉化、模型構建的綜合能力.問題難度適中,解析關鍵是將問題抽象或轉化為規則圖形的面積.
1.1 分步構建
教學中需要指導學生掌握該類問題的破解技巧,生成分步策略,建議分如下四步來構建:
第1步,找圓心,確定弧所對的圓心;
第2步,連半徑,連接圓心與弧上的點;
第3步,確定圓心角的度數,一般沒有提示則為特殊角,可以大膽猜想,嚴謹論證;
第4步,將不規則圖形的面積轉化為規則圖形的面積,構建面積模型,利用對應公式求解.
1.2 轉化方法
上述分步構建過程的第4步為解析關鍵,需要將不規則圖形轉化為規則圖形,教學中需要指導學生掌握相應的轉化方法,常見方法有如下三種:
方法1:構造和差法,將不規則圖形面積轉化為規則圖形面積的和或差;
方法2:等積轉化法,通過圖形變換,實現等面積轉換的方法策略,常與圖形運動相結合;
方法3:利用容斥原理,構建圖形面積的組合.
教學探究
對于與圓有關的陰影部分面積問題的專題探究,需要引導學生掌握分步構建策略,靈活使用轉化方法來簡化問題.上述總結了三種特殊的轉化方法,教學中需要深入解讀方法,并結合實例引導學生應用構建.
2 構造和差探究
構造和差法,表層含義為構造面積的和差,教學中需要挖掘其中的方法本質,即從整體上審視不規則圖形,將其視為規則圖形的一部分,則可以通過規則圖形的面積和差來構建,其中隱含了割補思想.
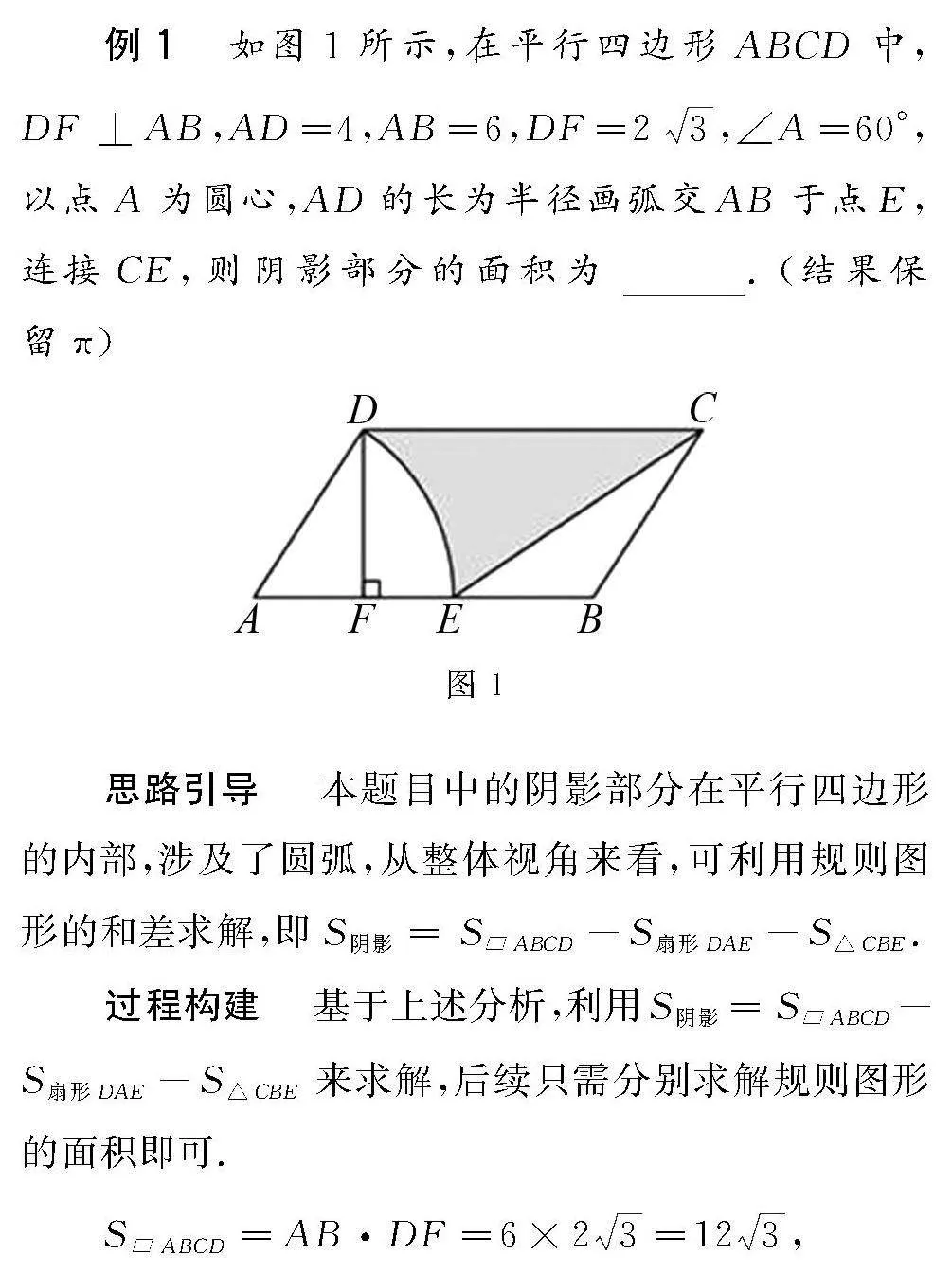
例1 如圖1所示,在平行四邊形ABCD中,DF⊥AB,AD=4,AB=6,DF=2 3,∠A=60°,以點A為圓心,AD的長為半徑畫弧交AB于點E,連接CE,則陰影部分的面積為 .(結果保留π)
圖1
思路引導 本題目中的陰影部分在平行四邊形的內部,涉及了圓弧,從整體視角來看,可利用規則圖形的和差求解,即S陰影=SABCD-S扇形DAE-S△CBE.
過程構建 基于上述分析,利用S陰影=SABCD-S扇形DAE-S△CBE來求解,后續只需分別求解規則圖形的面積即可.
SABCD= AB·DF=6×23=123,
S扇形DAE=60π·AD2360=83π,
S△CBE=12BE·DF=23,
綜合可得S陰影=SABCD-S扇形DAE-S△CBE=103-83π.
解后評析 上述題目利用的是構造和差求陰影部分的面積,從整體上審視圖形面積,從平行四邊形中剔除扇形、三角形的面積.教學指導的關鍵是理清圖中復合圖形的關系,從中提取規則圖形,再從整體視角構建.
3 等積轉化探究
等積轉化法,即進行等面積轉化的方法策略,教學探究的關鍵是等積轉化實現的途徑.總體上有兩種思路:一是根據面積公式構建等積轉化模型,二是結合圖形運動來轉化.
其中圖形運動轉化有平移轉化、對稱轉化和旋轉轉化三種,均是利用圖形三大運動的“不變”特性.教學中需要引導學生明晰轉化目的再探索轉化方案,即通過圖形運動實現“不規則”向“規則”的過渡.
例2 如圖2所示,在△ABC中,AB=AC,以AC為直徑的⊙O與AB,BC分別交于點D,E,連接AE,DE,若∠BED=45°,AB=2,則陰影部分的面積為 .(結果保留π)
圖2
思路引導 圖2中陰影部分可視為是兩部分,即線段AD將其分割為△ADE和圓弧圖形.
教學的關鍵是進行等積轉化構建,引導學生關注其中的△ADE,結合三角形面積公式分析△AOD和△ADE的面積關系,顯然兩者同底等高,則可以將陰影部分的面積轉化為扇形AOD的面積.
過程構建 連接OE,OD,如圖2的虛線所示.因為AC為⊙O的直徑,則∠AEC=90°.又知AB=AC,則BE=CE,即點E是BC的中點.因為點O是AC的中點,則OE是△ABC的中位線,可推知OE∥AB,從而可知S△AOD=S△ADE,所以S陰影=S扇形OAD.
通過角度分析,可知∠AOD=90°,則扇形的面積為S扇形OAD=90π·OA2360=π4,即陰影部分的面積為π4.
解后評析 上述題目利用等積轉化求陰影部分的面積,具體為局部等積轉化的策略,分為三步構建模型:第1步,將陰影部分圖形分割;第2步,結合面積公式對分割的三角形進行等積轉化;第3步,重組圖形,轉化為規則圖形.教學中需要指導學生掌握上述的等積轉化策略,即“分割→等積轉化→重組建模”.
4 容斥原理探究
利用容斥原理同樣可以求解陰影部分的面積,該方法適用于涉及基本圖形重疊的不規則面積求解,模型構建為:兩個基本圖形的面積-被重疊圖形的面積=組合圖形的面積.
教學中需要指導學生關注圖形特點,提取其中的重疊部分,再利用容斥原理來構建.
例3 如圖3所示,在Rt△ABC中,∠ACB=90°,∠B=30°,AB=2,以點A為圓心,AC的長為半徑畫弧,以點B為圓心,BC的長為半徑畫弧,兩弧分別交AB于點D、E,則圖中陰影部分的面積是 .(結果保留π)
圖3
思路引導 圖3中的陰影部分有兩段圓弧,直接進行面積和差組合不現實.教學中需要引導學生利用容斥原理來分析,關注其中的重疊部分,則陰影部分面積為扇形BCE與扇形ACD的面積之和與Rt△ABC的面積之差.
過程構建 在Rt△ABC,∠C=90°,∠B=30°,AB=2,則可求得∠A=60°,AC=12AB=1,BC=32AB=3.
而陰影部分的面積為S=S扇形BCE+S扇形ACD-S△ACB=30π·BC2360+60π·AC2360-12AC·BC=5π12-32.
解后評析 上述題目中利用容斥原理來求解陰影部分的面積,教學中需要引導學生關注扇形BCE與扇形ACD的面積的重疊情況,根據重疊部分與三角形的關系來構建模型.容斥模型在理解時存在一定的難度,教學中可以合理作輔助線,利用直觀圖形引導學生思考.
5 教學建議
上述綜合探究了陰影部分面積的破解策略,構建了分步構建方案,以及三種轉化方法.下面結合教學實踐開展教學反思,提出相應的教學建議.
5.1 梳理問題,分步構建
與圓有關的陰影部分面積問題,其特點為綜合了圓、三角形、四邊形等幾何圖形,幾何綜合性較強.教學中需要對常見情形進行梳理,指導學生明晰問題特點,再從題設條件入手來分析處理流程.上述總結了三步構建策略,教學說明中要注意三點:一是關注扇形、圓弧的處理技巧講解;二是關注線段、角度的推導分析;三是圖形拆解的處理方法.教學可以結合具體問題,引導學生按照“條件解讀→分析處理→模型構建→推導計算”的流程來處理問題.
5.2 方法探究,模型構建
上述總結了三大轉化方法,是不規則圖形面積的處理核心策略,教學中建議圍繞三大轉化方法深入探究.需要引導學生關注三點:一是方法的具體含義;二是結合解法構建模型;三是挖掘方法背后的深層內涵,包括方法本質和數學思想.教學時可以結合具體模型,利用模型來直觀講解,如構造和差轉化時,引導學生作輔助線來拆解不規則圖形,從整體視角來思考面積組合關系,進而構建面積模型.
5.3 實例精講,引導思路
“實例講解”是解法教學的關鍵環節,合理引導可以幫助學生強化理解方法.具體教學中不應注重講解的“量”,而忽視“質”,即注意實例精講,引導思路構建.以上述解法探究的實例講解為例,按照“思路引導→過程構建→解后評析”流程來開展,精選問題,首先引導學生分析問題,明確不規則圖形面積的轉化策略,再構建解題過程,解題后進一步引導學生反思,對解題過程與方法進行評析,完成解題的閉環.
5.4 探究拓展,素質提升
解法探究專題教學中,建議教師合理開展變式拓展,指導學生進行思維與能力的強化提升.該環節可以從以下兩個角度進行拓展:一是解法組合拓展,重新整合方法,如面積和差法的組合方式,針對同一問題,探索多種組合求解;二是綜合探究變式,如與三角函數、拋物線、網格等知識相結合.變式探究過程中,需注意思維引導,啟發學生思考,可以合理設置問題,分階段引導,充分鍛煉學生的思維.
6 結語
與圓有關的陰影部分面積問題的教學探究,要關注解題策略的構建,雖然問題相對較為簡單,但具體教學中,應注重方法的解讀與歸納.以學生為課堂探究的主體,引導學生充分思考,以“小問題”的講解,“窺探”類型題的本質,從而透視面積問題的解法.
參考文獻:
[1]李曉園.分步關聯突破,核心解法探究——以2022年宿遷市中考二次函數壓軸題為例[J].數學教學通訊,2023(35):82-84
[2]殷曼曼.重在課堂引導 構建數學思維——以“弧長及扇形的面積”課堂教學為例[J].中學數學,2023(24):47-48
[3]黎康麗.深度學習下支架式教學的探究——以“五步五環”法求陰影部分面積為例[J].中學數學教學參考,2023(20):14-16.

