初中數學結構化教學在初小銜接中的應用研究
在“雙減”背景下,新課標基于核心素養發展要求,對初中數學教學提出了新的要求。在課程內容結構方面,要求優化內容組織形式,加強學科間的相互關聯。結構化教學,是在“雙減”背景下,把握核心概念和關聯點,突出數學知識與思想方法的聯系,為推進深度學習而提出的一種教學方法。教師可借助結構化教學理念,聚焦知識結構的單元化呈現,將初中和小學的知識通過結構合理地銜接起來,打破初小銜接教學桎梏,以解決教學中的初小銜接難點問題,實現學生素養培育的螺旋式提升。
教育實踐表明,我國有相當比例的學生在小升初銜接時期存在不同程度的學習適應性問題。尤其是數學學科,隨著知識難度、深度的增加,對學生學習內容、學習能力、學習時間等方面的要求都有了較大的提升。如何引導學生盡快平穩、順利地適應初中數學學習,是亟待解決的問題。“雙減”政策是為了落實立德樹人的根本任務,要求以學生為本,堅持全面發展規律,優化學生學習結構,構建良好的教育生態。
一、概念界定:結構化教學與初小銜接
《義務教育數學課程標準(2022 年版)》指出:課程內容組織的重點是對內容進行結構化整合,探索發展學生核心素養的路徑。發展學生的數學核心素養,應著眼于知識結構的教學,開展促進核心素養發展的大單元結構教學。
美國教育專家、心理學家布魯納提出學習者要善于建構知識框架,并且學習的最終目的是形成一種良好的認知結構。2021 年,成宏喬、朱宸材在文章《結構化教學理念下的初中數學教學設計與思考———以“一次函數”章節復習課為例》中指出,以章節復習課為例,討論通過問題驅動式教學,按照知識結構、學習結構和教法結構的理念開展教學活動,以實現學生學習能力的提高。
結構化教學,是對相關教學內容進行統籌重組和優化,將優化后的教學內容視為一個相對獨立的結構形態進行呈現,以突出數學教學的整體性、結構性和關聯性的一種教學活動。在發展學生核心素養的理念下,結構化教學依據單元整體設計進行,以學生自我認知為前提,聚焦知識結構的單元化教學,在追求學生學科思維發展和學科能力提升的基礎上,建立適合學生學習和發展的結構化體系,幫助學生更輕松、有效地進行數學學習,以落實“雙減”減負增效的目標。
初小銜接,既要考慮課程知識之間的銜接,又要關注學生能力和素養的銜接。在銜接關鍵時期,教師不但要讓學生掌握數學基礎知識和技能,而且要引導學生理解舊知識與新知識的結構關聯性,以實現認知結構和思維結構的銜接,提升學生解決問題的能力。當前,中小學數學教材采用了“螺旋式上升”的方式,將數學知識合理地分散在不同的學段,教師如果對中小學的教材研讀不到位,就無法準確地把握數學知識的關聯性。教師應借助結構化教學理念,把握核心概念和關聯點,構建數學知識體系,幫助學生對數學知識與思想方法形成由點及面、由淺及深的結構化認知,并突破初小銜接教學桎梏,推進深度學習理念,以解決教學中的初小銜接難點問題。
二、目標定位:知識教學與素養提升雙線并進
目前,我國基礎教育學制大都是“六三三”制,教育教學工作在各學段分別進行,造成了當前研究多注重學生教育的階段性而忽視連續性,多注重層次性而較少關注整體性的現狀。教師在教學中,通過應用結構化教學模式,在發展學生核心素養的驅動下,以學生自我認知為前提,聚焦知識結構化呈現,建立適合學生學習和發展的結構化體系,幫助學生更輕松、有效地適應中學數學的學習。
義務教育階段,數學教材本身的知識結構是基本不變的,新課標基于核心素養發展要求,對初中數學教學提出了新的要求。在課程內容結構方面,要求加大學習內容與育人目標的聯系,優化內容組織形式。“雙減”政策要求教師在教學時要堅持以發展學生和培養學生為目標,幫助學生養成學科核心素養。
結構化教學是在新的教育背景下,為了提升學生的學習效果,促進學生深度學習而提出的一種教學方法。其強調將數學知識放在知識結構中,讓學生進行學習。教師通過結構化教學設計,可以凸顯知識的整體性、關聯性和邏輯性,幫助學生找到最近發展區,從知識結構的角度解決初小銜接問題,完善知識結構體系,以盡快適應初中數學生活,提高數學成績,促進數學素養的發展。
三、內容編制:小學知識和初中內容結構的整合
小學和初中是兩個不同的學段,對學生數學核心素養的培養,必須依靠各學段教育的相互銜接來完成。
(一)學段內容縱向結構對比
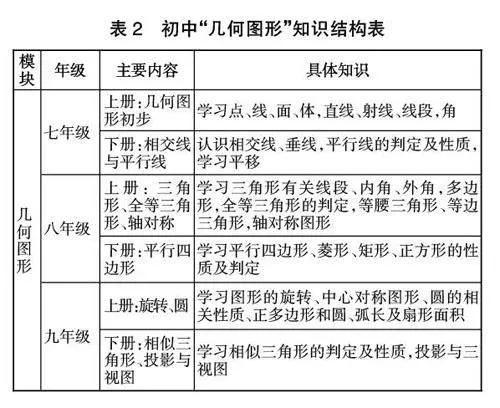
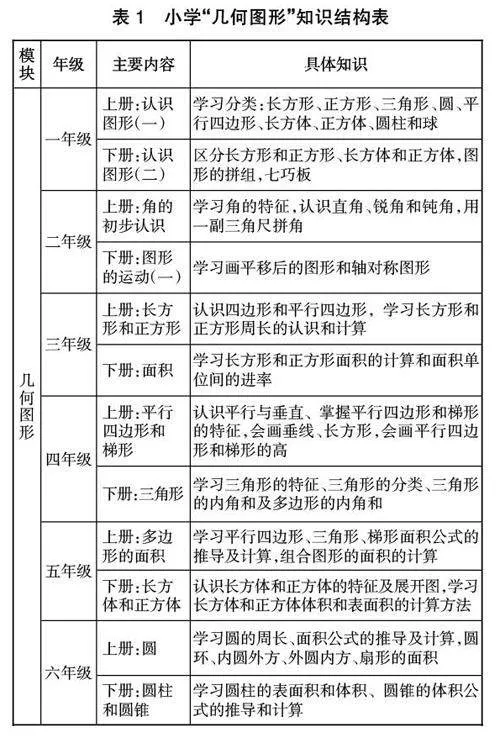
數學知識是有邏輯的結構體系,從縱向看,每一個知識點的呈現都是從易到難,螺旋上升的,貫穿整個小學、初中階段,學生對同一體系數學概念的理解呈遞進式的逐層深化趨勢。例如,在幾何內容學習中,從縱向看,對幾何圖形的認知發展貫穿整個小學階段(見表1)和初中階段(見表2)。
(二)知識內容橫向結構整合
從橫向看,每一個數學概念都不是孤立存在的,不同數學概念之間有機融合、互相影響,學生對相關聯的不同數學概念的理解在主題學習中形成結構化的認知。不同學段的教師要堅持以問題為導向,回歸教育規律,了解各學段內容的縱向結構,在日常教學中增強一體化意識,促進學段之間的銜接,提升學生數學學習的科學性。數學教師要積極探索和優化教學方式,以結構化數學知識為載體,在形成與發展“四基”“四能”的過程中,努力培養學生的核心素養。
通過師生問卷調查,了解“雙減”背景下小學、初中數學教師教學銜接的現狀,以及在教學銜接過程中存在的問題。通過對調查問卷數據進行分析,可以看出剛入初中的學生對數學的適應情況普遍一般,近半數教師認為學生基本適應,但也有相當一部分學生表示不太適應或很不適應。究其原因,教師認為主要有學習內容的增多和難度的加大、小學與初中教學方法的差異、學習方法的不適應等。為了幫助七年級新生更快地適應初中數學,建議中小學數學教師熟知兩個學段的知識體系,前期適當放慢教學節奏,指導學生使用正確的學習方法,喚起學生學習數學的興趣。
四、案例研究:教學實踐與循證研究螺旋遞進
在“雙減”政策下,結合調查數據發現,根據中學生的身心發展特點,開發結構化教學樣板單元課程,開展結構化教學模式案例研究,應用“整體—結構”教學模式進行案例教學設計,探索“雙減”背景下初小銜接中運用結構化教學模式是有效的。在案例研究實施中,教學目標的設定體現整體性和階段性,基于課程設計整體把握教學內容,注重知識點的結構化整合。
(一)單元統整,串聯要素
教師在教學的過程中要基于初中數學知識的整體性開展教學活動,例如,學習八年級第十一章到第十三章的內容時,需要循序漸進學習“三角形”“全等三角形”及“軸對稱”三個章節。基于結構化教學理念,教師要引導學生從三角形的特征、與三角形相關的線段、相似三角形的判定及等腰三角形等要素進行相關性學習,以結構化的方式為學生講授,提升學生對三角形知識的學習與應用能力,提高學生對數學知識的理解水平和遷移能力。
(二)聯系舊知識,進行關聯融合
在初中數學教學中,引導學生聯系之前的舊知識,關聯融合新知識點,提升學生的學習效果。例如,古代數學“雞兔同籠”問題,是小學數學的一個經典題型,是一個包含隱藏數字的問題,而解題的關鍵就是找到題目中隱含的數字。在教學“二元一次方程組”時,教師可重拾“雞兔同籠”問題,聯想小學解題時運用的邏輯推理方法進行探究,通過分析數量關系,把算術思維轉變成代數思維,利用二元一次方程組輕松解決小學時期的難題。同課異構的設計,可以幫助學生更深入地理解和掌握二元一次方程,從而達到關聯學習、融合發展的目的。
(三)鏈接建構,拓展遷移
為了培養學生的數學核心素養,初中數學教師在結構化的教學模式中,要將一些新的關聯性教學內容融入課程教學中,幫助學生養成數學遷移能力。例如,在教學“二元一次方程組”時,為了培養學生的數學遷移能力,教師可以根據學生學7FcxzKOTVKEimhXo3Ld9ZQ==情,嘗試選學“三元一次方程組”的解法,讓學生在內容拓展的過程中鞏固和強化“二元一次方程組”的解法和步驟。
五、評價管理:學習過程與評價呈現一體融入
(一)依托教材體系,把握學習起點
運用“整體—結構”教學模式時,教師可以借鑒格蘭特·威金斯和杰伊·麥克泰格兩人提出的逆向教學設計理論,設計相應的課堂實踐程序,實現“教—學—評”一體化。以學習目標為起點,確定評價標準和評價任務,再根據學習目標設計學習活動。教師在活動組織中認真收集評價信息,利用工具分析評價結果,依據評價結果審視目標達成情況,再根據反饋的學習信息,調整學習目標,形成新評價、新活動。通過實施“編制—實施—評價—更新”的教學規劃,實現“教—學—評”三位一體,循環反復,不斷改善教與學的水平,讓學習真實發生。
(二)歸類統整設計,促進方法遷移
結構化整合是基于學生立場、單元視角進行有機整合、適度拓展,要求基于數學本質,豐富其知識內涵。例如,在教學“圓的有關性質”時,由于學生在學習之前已對圓有豐富的認知,本單元的統整目的在于通過系列化的自主學習、教師引導學習,促進學生自主地運用圓的相關知識解決問題,達到內化、遷移的目的。教師通過以核心任務為統整的單元項目探究任務單及其分解任務,促使學生自主、積極、深入地在操作、思考中感悟、認知圓的核心概念,促進單元結構化學習。
(三)優化活動設計,落實評價任務
指向結構化核心目標,關聯現實世界需求,設計構建單元結構化項目實踐課,讓學生在玩中學,學中用。例如,在教學相似三角形相關知識后,在實踐中利用相似三角形單元的整體知識做遷移、拓展,有利于學生進行深入的思考,提升學生的數學思維、空間意識和應用意識。根據評價任務,形成系列學評活動,將其嵌入教學過程,利用統整分析促進教學方案的改進。
六、結語
結構化教學是在“雙減”背景下,把握核心概念和關聯點,突出數學知識與思想方法的聯系,為推進深度學習而提出的一種教學方法,它強調將學科知識放在結構整合中讓學生進行學習。教師通過實施結構化教學,可以帶動數學教學的高質量實施,實現從“知識本位”走向“素養追求”的課程改革,提高育人效能,實現素養培育的循序漸進和螺旋上升,讓學生在初中數學課堂中能夠得心應手地學習。

