例談空間幾何體的“降維”方法

【摘要】空間幾何體是高中數學立體幾何板塊的重要研究對象，是空間中點、線、面位置關系的主要載體．空間幾何體的“降維”分析，即將空間立體幾何問題轉化為平面幾何問題，是研究立體幾何的一般方法，亦可培養學生的化歸轉化能力和直觀想象素養．

【關鍵詞】空間幾何體;“降維”分析;化歸轉化;直觀想象

高中數學的立體幾何問題，尤其是與幾何體有關的問題，常常需要轉化為平面圖形進行分析，本文稱之為“降維”．幾何體中常見的夾角問題、截面形狀問題、距離問題、位置關系問題以及動點的軌跡問題，大都可以通過適當轉化得以簡化．本文主要提出三種“降維”分析的角度，以供讀者參考、討論、補充．

1“降維”方式1：展開

例1長方體ABCD-A1B1C1D1中，AB=2，BC=3，AA1=5，一只小蟲從A點沿長方體的表面爬到C1點，求小蟲經過的最短距離．

分析求最短路徑問題，一般方法是將幾何體的表面展開，進而分析平面上兩點的最近距離，然后再還原為幾何體．本題中，將長方體兩頂點A和C1置于同一平面的展開方式有如上三種．如圖1-1、圖1-2和圖1-3：

在上面三個展開圖中，連結AC1即為最短路徑，分別計算得到：

圖1-1中，AC1=（2+3）2+52=50=52；

圖1-2中，AC1=（2+5）2+32=58；

圖1-3中，AC1=（5+3）2+22=68；因此，本題小蟲經過的最短距離為52．

例2在長方體ABCD-A1B1C1D1中，AB=2，BC=AA1=1，點M為AB1的中點，點P為對角線AC1上的動點，點Q為底面ABCD上的動點（點P，Q可以重合），求MP+PQ的最小值.

圖2分析本題所求為空間中兩條折線段的長度之和，也是一種距離問題，考慮將兩條直線所在的平面展平為同一平面從而實現“降維”．圖2中，由于點Q為底面ABCD上的動點，因此指定一點P，則PQ最小時點Q應為P在底面ABCD上的投影，即有PQ⊥平面ABCD，故點Q在截面ACC1A1上，即Q在AC上．考慮將平面AB1C1和平面ACC1展為同一平面，如圖2-1，在這一平面上求兩條折線段距離，易得最小位置應為圖2-2所示，即點M，P，Q共線且有MP⊥AC．結合題目已知條件，△AB1C1≌△ACC1且易得∠C1AC=∠B1AC1=30°，且有AM=12AB1=32，故所求最小值為MQ=AM·sin 60°=34．

展開圖是將空間幾何問題平面化最為直接的方法之一，通過這樣的方式，我們可以將立體幾何問題轉化為平面幾何問題，借助平面幾何有關定理即可得解．

2“降維”方式2：截面

圖3例3如圖3，正方體ABCD-A1B1C1D1的棱長為23，動點P在對角線BD1上，過點P作垂直于BD1的平面α，記這樣得到的截面多邊形（含三角形）的周長為y，設BP=x，則當x∈［1，5］時，求函數y=f（x）的值域．

分析本題涉及到正方體中垂直體對角線的截面問題．圖3中所示三角形應為平行于平面AB1C的等邊三角形，因此隨著x增大，三角形周長也在不斷增大，直至△AB1C處．x繼續增大，截面開始出現六邊形，如圖3-1，此時六邊形的六條邊可以看成三對，每一對即為圖中的MN和NQ.實際上，MN+NQ的值始終等于AB1，可參考圖3-2理解，也就是說，截面雖然變為六邊形，其周長并沒有改變，直至截面再次轉為△A1DC1，而后周長逐漸變小．因此不難得出，當x∈［1，5］時，函數y=f（x）的值域為［36，66］．

例4正方體ABCD-A1B1C1D1的棱長為1，點P，Q，R分別是棱A1A，A1B1，A1D1的中點，以△PQR為底面作正三棱柱，若此三棱柱另一底面三個頂點也都在該正方體的表面上，求這個正三棱柱的高.

圖4分析例題3的設問直接指向了幾何體的截面問題，我們只需要對截面的特征熟練掌握即可，而本題的問題需要我們轉化為截面問題．如圖4，根據前面的分析，我們很容易判斷出平面PQR平行于平面AB1D1，因此三棱柱另一底面必然也與平面AB1D1平行．此外，在正方體中，還有A1C⊥平面AB1D1，因此正三棱柱的三條側棱都與A1C平行，取其中一條研究，不難將問題轉化為：過圖4中的P點，求作直線A1C的平行線，故問題只需要在點P和直線A1C所在的平面上研究.進一步地，在△A1AC中，取AC中點T，則必有PT∥A1C，因此正三棱柱的高即為PT=12A1C=32．

在例題3和例題4中，分別用到了幾何體的截面圖，相對于展開圖，截面圖更多的用于定性分析之后的“降維”操作，也就是說，我們已經對題中的線線關系或線面關系有了具體的認識，而后根據其所在的截面進行進一步分析．

實際上，幾何體的截面問題是非常好的空間想象能力訓練的素材，以正方體為例，其特殊截面如圖4-1所示，可以根據具體問題再行補充．

3“降維”方式3：投影

新教材[1]中弱化了對幾何體三視圖的要求，但在很多情境中，將幾何體或某條直線投影到特定平面之后分析仍然會對計算有所簡化．

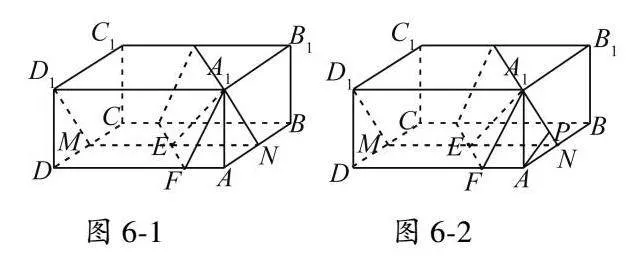
例5如圖5，在棱長為2的正方體ABCD-A1B1C1D1中，E為BC的中點，點P在線段D1E上，求點P到直線CC1的距離的最小值．

分析本題涉及異面直線間的距離，一般來說應通過空間向量解題，但此法運算起來較為復雜，因此可以考慮將問題進行“降維”分析，點P到直線CC1的距離，可以考慮將點P沿CC1的方向投影到底面A1B1C1D1上，即圖5-1中，取B1C1中點E1，連結EE1，P在D1E1上的投影為P1，因此本題轉化為求P1到直線CC1的距離最小值，即P1C1的最小值，很明顯，過C1做D1E1的垂線，垂足即為所求位置，答案為255．

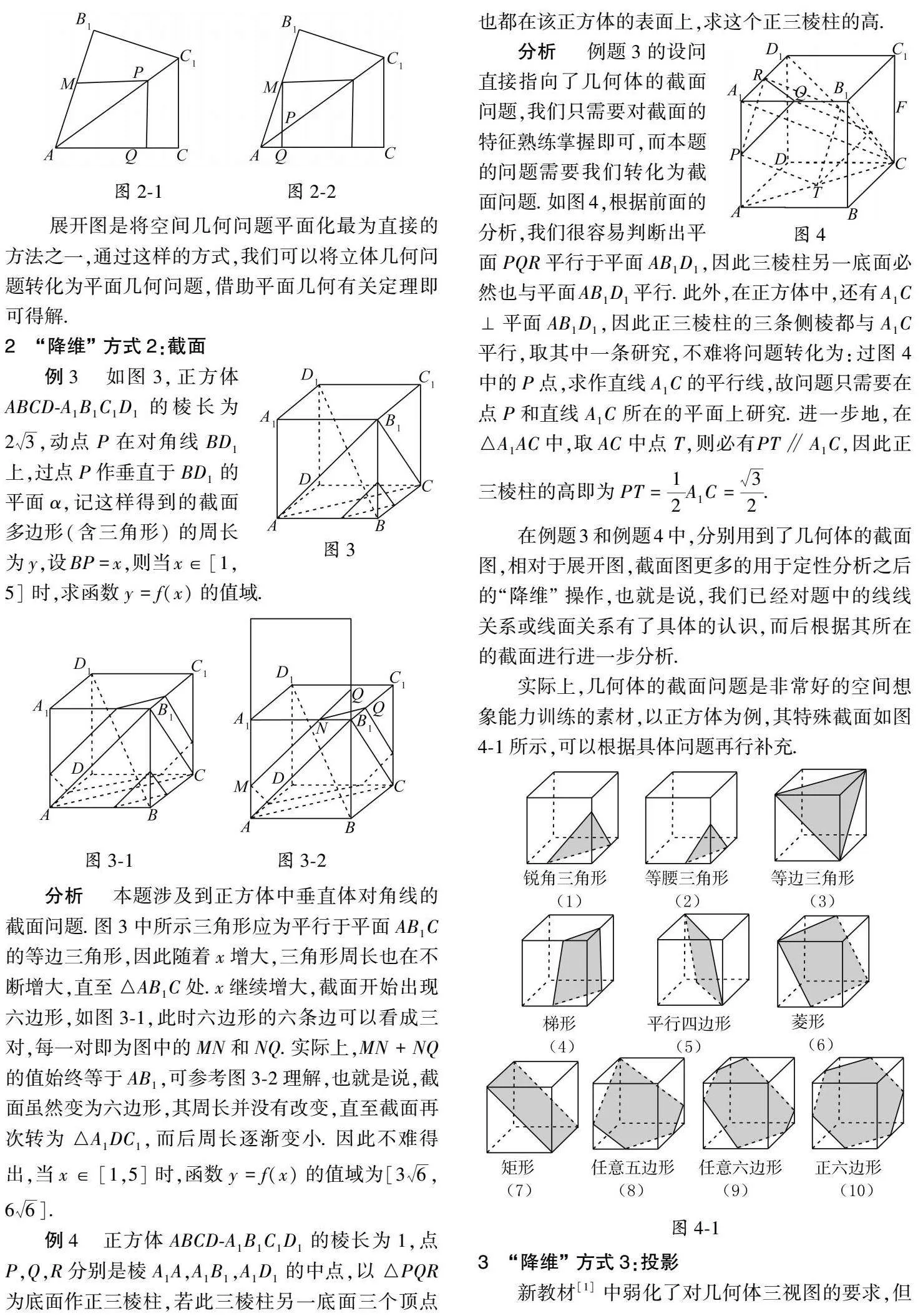
例6如圖6所示的一塊長方體木料中圖6，已知AB=BC=4，AA1=1，設E為底面ABCD的中心，且AF=λAD，（0≤λ≤12），求該長方體中經過點A1，E，F的截面面積的最小值．

分析由題意，點F在線段AD上運動，將經過點A1，E，F的截面補全如圖6-1所示，其面積即為△A1EF面積的四倍，因此問題轉化為求△A1EF的面積．易得A1E=3，故只需計算點F到A1E的距離的最小值，因此需要構造一個過直線A1E的平面，使之與直線AD平行，即圖6-1中的平面A1D1MN．求點F到平面A1D1MN投影的距離，即求點A到平面A1D1MN的距離，即點A到A1N的距離，如圖6-2中，過點A做A1N的垂線，交A1N于P，線段AP=255即為F到平面A1D1MN的距離，也是F到A1E的距離的最小值，因此所求截面面積的最小值為1255．

這里所提到的投影，實際上是通過對題意的轉化，將題中所求的距離問題轉化為其他特殊點到投影面的距離，進而轉化為點到直線的距離．在涉及其他空間位置關系時，也可以通過將幾何體投影到指定平面進行分析，例如研究異面直線夾角問題，運用三垂線定理解決線面關系等等，這些問題都比較熟悉，此處不再展開．

以上的三種“降維”方法是分析空間幾何體中位置關系和數量關系的常用方法，“立體問題平面化”是我們分析復雜幾何體問題的首要思考方向，通過展開圖、截面圖和適當的投影可以將問題進行轉化或簡化；“平面問題三角化”實際上是轉化后的繼續分析，例如平面幾何中的正、余弦定理，平面向量甚至是解析幾何，都可以恰當的融入其中，這在本文中的幾道例題中均有充分的體現．

當然，解決立體幾何問題的方法還有很多，例如平移、延展、截割、補形、構造輔助幾何體以及運用空間向量等等，無論是哪種方法，其根本抓手都是空間幾何體的基本性質以及空間點線面的基本結論，只有熟知這些基本內容，掌握研究立體幾何的基本方法，才能不斷生發出新的解決問題思路，從而恰當的運用化歸轉化思想使問題得以簡化，進而不斷運用平面幾何中的素材強化空間幾何問題的直觀想象素養[2]．

參考文獻

[1]人民教育出版社，課程教材研究所，中學數學課程教材研究開發中心. 普通高中課程標準實驗教科書·數學：B版[M]. 北京： 人民教育出版社，2020.

[2]章建躍. 樹立課程意識，落實核心素養[J]. 數學通報，2016，55（05）：1-4.

作者簡介

崔鵬（1984—），男，北京人，中學高級教師、年級組長、北京數學會會員、北京市骨干教師、海淀區學科帶頭人；研究方向為數學課堂教學、教材教法分析以及數學學科德育理論研究與課堂實踐.

基金項目

北京市海淀區教育科學“十四五”規劃課題“深度學習視域下的數學教學情境建構與應用”（HDGH20230373）.