一次函數背景下“一線三等角”模型的應用探究

【摘要】“一線三等角”模型是初中數學非常重要的一個模型，一次函數也是初中數學非常重要的內容，本文旨在一次函數背景下，通過“一線三等角”模型分析并解決問題，從而更好地滲透數形結合、分類討論等數學思想方法，為培養學生的幾何直觀、邏輯推理等核心素養奠定基礎.

【關鍵詞】一線三等角；一次函數；初中數學

1 引言

代數與幾何是中學里非常重要的知識，初中數學更是以二者為主，多地中考數學考試常出現以“一線三等角”模型解決問題的題目，這類題目既考查學生對基礎知識和基本技能，又考查學生數形結合、分類討論等數學思想方法的運用，還檢驗學生的幾何直觀、邏輯推理等核心素養[1].

2 真題呈現

例1 （2022年安徽省中考試題填空題最后一題[2]）如圖1，四邊形ABCD是正方形，點E在邊AD上，△BEF是以E為直角頂點的等腰直角三角形，EF，BF分別交CD于點M，N，過點F作AD的垂線交AD的延長線于點G，連接DF，請完成下列問題：

（1）∠FDG=°；

（2）若DE=1，DF=22，則MN=.

上述真題是“一線三等角”模型在初中數學問題中一次精彩的應用，教學中，及時歸納如“一線三等角”等數學模型，注重培養學生的模型觀念，有利于增強學生的數學能力，提升學生的數學核心素養[3].

3 模型提取

類型1 同側一線三等角

點P在線段AB上，∠1=∠2=∠3，圖2中的三等角為銳角，圖3中的三等角為直角，圖4中的三等角為鈍角.

類型2 異側一線三等角

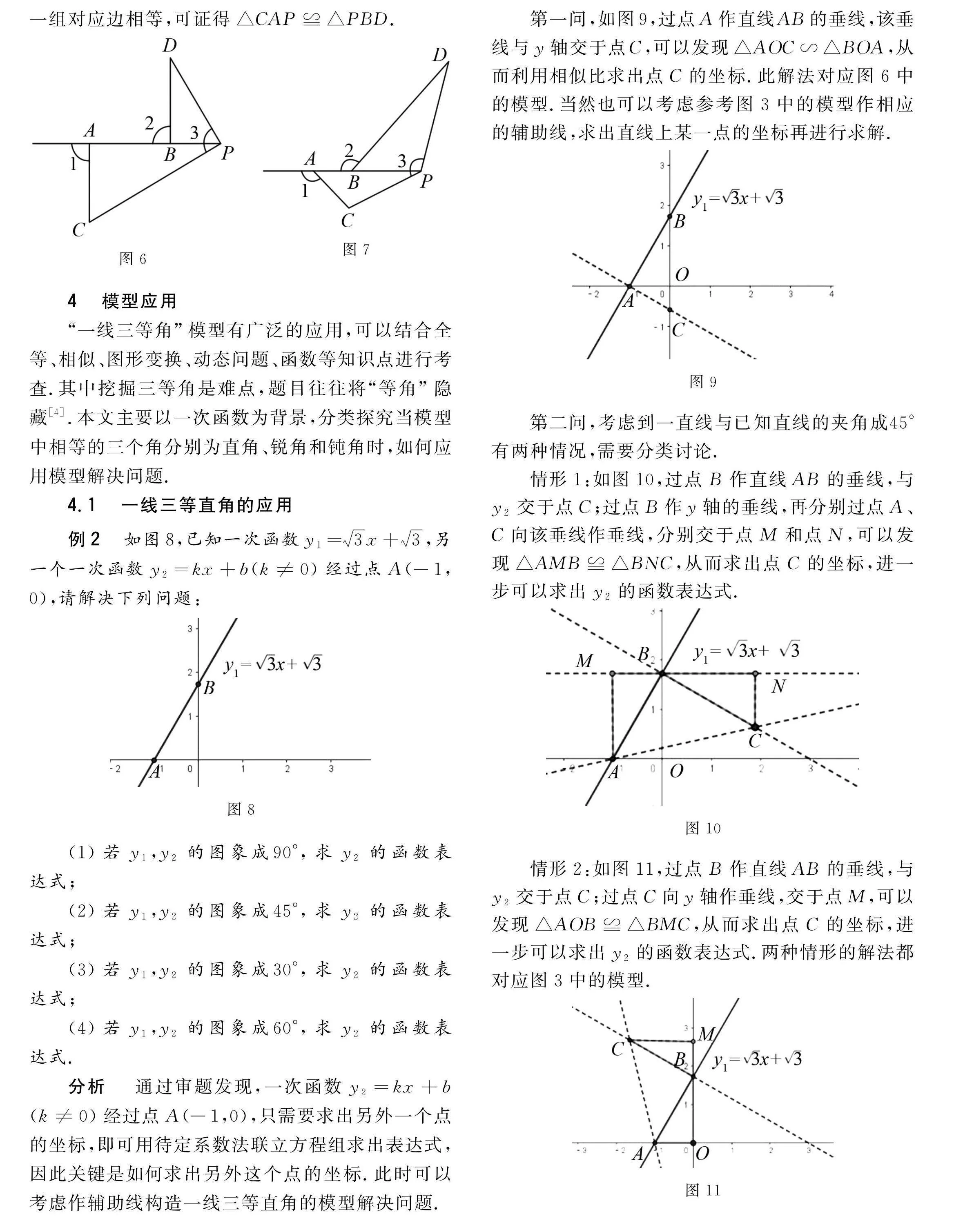
點P在線段AB的延長線上，∠1=∠2=∠3，其中∠1，∠2居于直線AB的兩邊，∠3為∠CPD，圖5中的三等角為銳角，圖6中的三等角為直角，圖7中的三等角為鈍角.

上述每一個圖形中都可以證得△CAP∽△PBD.若由一般到特殊，在已知條件中添加任意一組對應邊相等，可證得△CAP≌△PBD.

4 模型應用

“一線三等角”模型有廣泛的應用，可以結合全等、相似、圖形變換、動態問題、函數等知識點進行考查.其中挖掘三等角是難點，題目往往將“等角”隱藏[4].本文主要以一次函數為背景，分類探究當模型中相等的三個角分別為直角、銳角和鈍角時，如何應用模型解決問題.

4.1 一線三等直角的應用

例2 如圖8，已知一次函數y1=3x+3，另一個一次函數y2=kx+b（k≠0）經過點A（－1，0），請解決下列問題：

（1）若y1，y2的圖象成90°，求y2的函數表達式；

（2）若y1，y2的圖象成45°，求y2的函數表達式；

（3）若y1，y2的圖象成30°，求y2的函數表達式；

（4）若y1，y2的圖象成60°，求y2的函數表達式.

分析 通過審題發現，一次函數y2=kx+b（k≠0）經過點A（－1，0），只需要求出另外一個點的坐標，即可用待定系數法聯立方程組求出表達式，因此關鍵是如何求出另外這個點的坐標.此時可以考慮作輔助線構造一線三等直角的模型解決問題.

第一問，如圖9，過點A作直線AB的垂線，該垂線與y軸交于點C，可以發現△AOC∽△BOA，從而利用相似比求出點C的坐標.此解法對應圖6中的模型.當然也可以考慮參考圖3中的模型作相應的輔助線，求出直線上某一點的坐標再進行求解.

第二問，考慮到一直線與已知直線的夾角成45°有兩種情況，需要分類討論.

情形1：如圖10，過點B作直線AB的垂線，與y2交于點C；過點B作y軸的垂線，再分別過點A、C向該垂線作垂線，分別交于點M和點N，可以發現△AMB≌△BNC，從而求出點C的坐標，進一步可以求出y2的函數表達式.

情形2：如圖11，過點B作直線AB的垂線，與y2交于點C；過點C向y軸作垂線，交于點M，可以發現△AOB≌△BMC，從而求出點C的坐標，進一步可以求出y2的函數表達式.兩種情形的解法都對應圖3中的模型.

第三問、第四問類比第二問，依然需要分類討論，但各需排除一種與坐標軸垂直的情況，利用三角形的相似性來求出點C的坐標，進一步可以求出y2的函數表達式.

上述例題中，要求的一次函數是經過已知的一次函數上的某一點，如果考慮要求的一次函數，經過的不是已知一次函數上的某一點，該怎么解決呢？

例3 已知一次函數y1=3x+3，另一個一次函數y2=kx+b（k≠0）經過點C（m，n），點C不在y1上，考慮例1中的四種情況，分別求出相應的一次函數y2的函數表達式.

分析 雖然未知的一次函數經過的是已知直線外的一點，但是仍然可以先考慮經過點A的情形（當然也可以是已知直線上任意一點），再根據已知的點C的坐標，進一步求出b的值.這種轉化與化歸的數學思想方法經常在初中數學學習中用到.

4.2 一線三等銳角的應用

例4 如圖12，已知△AOB為等邊三角形，點C和點D分別在線段OA和線段AB上， 將△ACD沿直線CD翻折，使點A落在線段OB上于點E，△OCE和△BDE的面積分別是S1和S2，若S1∶S2=4∶9，OB=6，求直線CD的函數表達式.

分析 由題意可知解題的關鍵是求出點C和點D的坐標.通過審題判斷含有如圖2中的一線三等角模型，可知△OCE∽△BED，由S1∶S2=4∶9可知相似比為2∶3，從而可以設未知數求解.不妨設BE的長為3x，由相似比以及△AOB為等邊三角形可以分別表示出OE、OC、CA、CE、BD、DA、DE，從而求出線段OC和線段BD的長，再利用△AOB為等邊三角形，∠B=∠AOB=60°，分別過點C和點D向x軸作垂線可以構造兩個含有60°內角的直角三角形，進而可以求出點C和點D的坐標，從而可求出直線CD的函數表達式.

4.3 一線三等鈍角的應用

例5 如圖13，已知四邊形ABCD為等腰梯形，∠D=60°，點O和點E分別在線段BC和線段DC上，∠AOE=120°，OB∶OC=2∶1，BC=BA=6，求線段OE所在直線的函數表達式.

分析 由題意可知解題的關鍵是求出點E的坐標，通過審題判斷含有如圖4中一線三等角模型，可知△ABO∽△OCE，利用相似比可以求出CE的長，再利用∠D=60°，可知過點E向x軸作垂線可以構造一個含有60°內角的直角三角形，進而求出點E的坐標，從而求出直線OE的函數表達式.

5 結語

通過上述問題的探究，我們可以感受到一線三等角模型在一次函數背景下應用的廣泛性.用該模型考驗學生可以很好地滲透幾何直觀、邏輯推理等核心素養.本文只是以一次函數為背景，對一線三等角模型的應用進行了探究，各位讀者也可以從其他角度進一步進行思考.

【基金項目：泰州學院課程思政示范課程建設項目“運籌與優化”（20KCSZ09）】

參考文獻：

［1］中華人民共和國教育部．義務教育數學課程標準（2022年版）[M]．北京：北京師范大學出版社，2022．

[2]劉敏.巧用“一線三等角”模型 突破幾何壓軸難題[J]．中學數學，2022（22）：60-61+64．

[3]曹喜榮．“一線三等角”問題的探究和拓展——以2022年中考數學安徽卷第14題為例[J]．中學數學教學，2023（03）：55-56．

[4]劉玲．正方形背景下“一線三等角”模型的探究[J]．中學數學教學參考，2023（12）：34-36．