初三數學專題復習課的教學設計探析

【摘要】初三數學總復習是將整個初中階段數學知識點系統化、深化并運用數學基本思想與數學方法解決有關問題，為學生應對中考做充足準備.本文以一節初三專題復習課公開課為例，闡述初三數學專題復習課的教學策略.

【關鍵詞】垂直問題；初中數學；解題教學

1 專題復習課的概述及必要性

復習課大致可分為章節復習課、期中期末復習課和專題復習課.在結束初三新課后，將知識點系統復習尤為關鍵.而初三畢業班總復習可分為一輪復習和二輪復習，二輪復習一般以專題復習課為主.初三數學專題復習課指根據考試大綱的要求，將主要考點分成若干個專題，每個專題結合所學的相關知識點，以問題為主要線索，課上對學生進行專題訓練，并提煉出不同題型的解題技巧及方法.這些專題可以將零散的相關知識點進行系統整合，進一步加深學生對數學內在知識體系的建構和對同類數學問題的方法提煉，保證學生在有限的時間內綜合、全面地鞏固、掌握數學知識，這樣使得學生更從容備戰中考.

2 教學實踐重現

本節公開課是去其他學校借班上課，在對學校和學生都不熟悉的情況下，筆者在正式上課前讓學生抽時間完成學歷案的第1題并進行批改.一方面可以，提前熟悉學生名字并了解該班學生數學學習水平；另一方面課上有一道挑戰題，需要給學生充足思考時間，這樣整節課的節奏容易把握，不至于很倉促.筆者將本節公開課的課題取名為“Once More”，面對素未謀面的學生，先請英語課代表解釋課題的中文意義，起點低，拉近與學生之間的距離.

2.1 情境再現：用垂直

師 今天的課題可以理解為垂直再現或再次學習探究垂直.為什么說是再次探究垂直呢？大家回顧下，在八年級的學習內容中，關于垂直可以聯想到直角三角形.那么關于直角三角形我們學習了哪些內容呢？

生 勾股定理及其逆定理.

師 今天我們站在整個初中數學角度上，重新認識垂直.

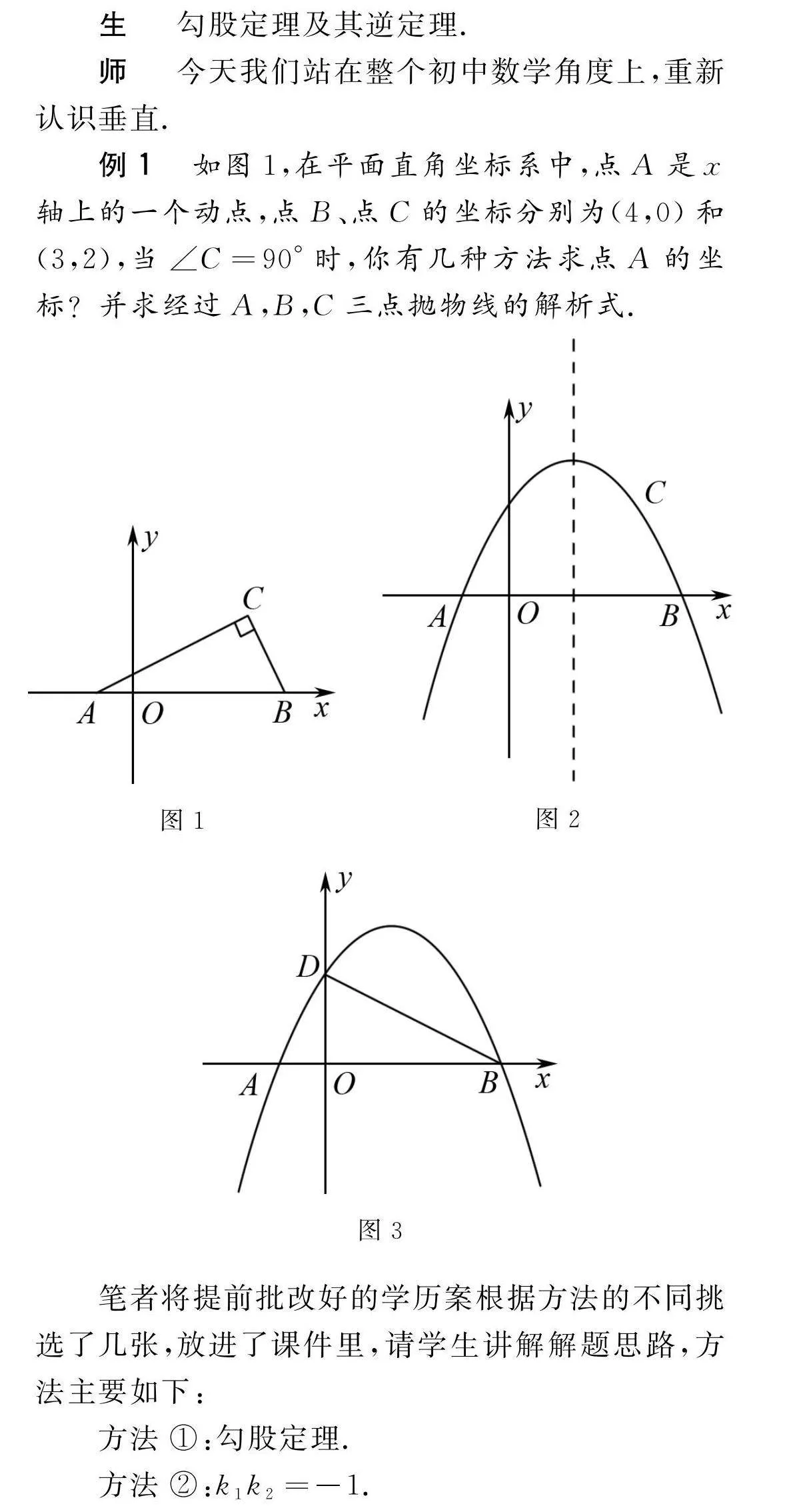
例1 如圖1，在平面直角坐標系中，點A是x軸上的一個動點，點B、點C的坐標分別為（4，0）和（3，2），當∠C=90°時，你有幾種方法求點A的坐標？并求經過A，B，C三點拋物線的解析式.

筆者將提前批改好的學歷案根據方法的不同挑選了幾張，放進了課件里，請學生講解解題思路，方法主要如下：

方法①：勾股定理.

方法②：k1k2=-1.

方法③：三角函數.

方法④：相似（k型相似、射影定理）.

小結

師 上述幾種方法都是“用垂直”進行解題，方法①②是直接利用垂直條件解題，方法③④是通過輔助線構造新的直角三角形.

師 追問方法③④添加完輔助線，新直角三角形的直角邊和原直角三角形的直角邊與坐標軸在位置上有什么區別？

生 原來直角三角形的直角邊是傾斜的，新的直角三角形直角邊與坐標軸平行或重合.

師 給出方法③④的解題技巧是“改斜歸正”.我們經常把斜垂直問題轉化為正垂直.在求出點A坐標的基礎上，再求經過A，B，C三點拋物線的解析式就顯得比較容易，根據交點式求解即可.

2.2 鞏固提升：辨垂直

例2 如圖2在例1的基礎上，若點P是對稱軸上的一個動點，判斷是否存在點P，使得△PBC是以BC為斜邊的直角三角形，并說明理由.

此環節需要學生完成在學習單第2題，先獨立思考，再同桌之間交流討論.教師巡視，先挑選“用垂直”的1～2種方法，請學生講解大致思路.

師 其實方法①是先假設點P存在，再“用垂直”求解.

生1（信心滿滿地） 題目中“以BC為斜邊的直角三角形”說明BC邊對的角是直角，說明點P的運動軌跡是一個以BC為直徑的圓，根據定弦對定角，直徑所對的圓周角是直角.點P已經在圓上，至于點P是否在對稱軸上，只需判斷對稱軸和圓有沒有交點就可以了.這樣就轉化為直線與圓的位置關系，只需判斷圓心與對稱軸的距離d與半徑r的大小關系.如果d ≤ r，有交點，說明點P存在；如果d大于r，沒有交點，說明點P不存在.

生2 補充：計算出d等于2，半徑r等于52，可以得出d＞r，圓和對稱軸沒有交點，說明點P是不存在的.

師小結 大家分析得十分到位.遇到辨“垂直”是否存在的問題，除了“設存在+驗證根”這一方法，還可以用“尋軌跡+辨交點”的方法快速求解.這里用到了什么數學思想方法呢？

眾生（異口同聲地） 數形結合.

2.3 挑戰提升：覓垂直

例3 如圖3點D是拋物線與y軸的交點，點Q是拋物線上的一個動點，若以Q，D，B三點圍成的三角形是直角三角形，求出點Q的坐標.

此環節需要學生完成學習單的第3題，獨立完成后，四人小組內進行討論.教師巡視，并給予一定指導.難點在于∠Q=90°時，學生不會解一元三次等式，引導學生因式分解后求解.

生3（上臺講解） 要分3種情況，點Q，D，B都有可能是直角頂點.當點D是直角頂點時（或∠QDB=90°），點Q恰好在點A上，可以根據勾股定理或k1k2=-1或相似等證明此時三角形QDB是直角三角形；當點B是直角頂點時（或∠QBD=90°），可以用垂直（構造K型相似等）得到一元二次方程，從而解出點Q的坐標；第三種情況，當點Q是直角頂點時（或∠BQD=90°），用軌跡法可以確定點Q的大致位置，再“用垂直”的方法得到一元三次方程，這個方程不太好解，可以先因式分解，約去x- 4，得到一元二次方程，得到Q的橫坐標是1，從而得到點Q的坐標（1，3）.

師小結 像遇到第3題這樣求點的坐標的，我們一起來總結下步驟吧.

①先分類；②通過“辨垂直”確定點的位置；③“用垂直”求點.

3 專題復習課的教學設計的思考

3.1 專題復習課的特點

上海市徐匯區教研員、中考命題組專家張斌輝老師曾說過：“專題復習課的特點應該是‘小’‘專’‘低’.”“小”指的是切入點小，如本節課以平面直角坐標系中直角三角形斜放問題作為切入點，這個問題學生平時做題時經常會碰到.“專”指的是專題復習課是專門解決同一類問題，本課解決了平面直角坐標系中斜垂直問題，可以將斜垂直問題轉化為正垂直，出現直角可以聯想到勾股定理、斜率乘積為-1、三角函數、相似、圓軌跡等，從而提煉出針對這一問題的方法技巧，在上課時間允許的情況下適當變式訓練，進一步培養學生舉一反三的能力.“低”指的是起點低，因為不是只涉及部分學習能力強的學生，而要面對全體學生，所以一開始提出的問題難度低，容易被所有學生接受，便于激發學生學習數學的興趣，對活躍課堂教學氛圍起到一定積極的作用.如本課學習單中的例1較簡單，班級里的后進生至少能寫出一種方法.筆者課前批改時發現優等生能想出三四種方法，基于此，在設計學習單過程中對于例1就設計了3個備用圖，培養學生的發散思維.

3.2 專題教學的問題設計

初三復習時間緊張、任務繁重，數學教師既要分出專題，又要精心選擇或自擬典型例題，還要高效開展課堂教學.專題復習課的例題設計是整節課的生命線，例題選取的好壞直接影響專題復習課的成功與否.為了提高復習效率，教師需要根據教材，結合考試大綱，在例題選取時注意以下三點：

一是要有典型性.復習課的落腳點應該回歸教材，專題復習課的問題以教材中的例題為原型，緊扣考點，對問題進行變式拓展，做到一題多解、多題一解.如本課中的例1存在多種解法，幫助學生鞏固勾股定理、斜率之積為-1、三角函數、相似等與直角相關的知識點.在讓學生講解方法的過程中，調動了學習積極性.縱觀本節課，三道例題是同一種類型的題目，屬于平面直角坐標系中的垂直問題，每道例題之間應具有一定的連貫性和邏輯性，從而能夠提煉出平面直角坐標系中的垂直問題的解題方法.

二是要有層次性.不得不承認初三學生的差異比較大，專題復習課設計的問題串應該適應不同層次的學生，難度由淺入深、循序漸進，讓不同層次的學生得到不同的發展.本課的起點較低，對于已結束初三新課的學生而言，想出一兩種方法解決例1并不難，做到人人都能夠參與課堂中.對于緊接著的例2和例3，想出一種方法或一兩種情況也不難，但要考慮到所有方法或情況都有一定難度，對于大部分學生來說是一種挑戰，實踐表明，只有部分優等生能做出.

三是要有開放性和探索性.學生通過開放性問題的探索與鉆研，提高發現問題、分析問題、解決問題的能力.開放性問題可以是一題多解，或需考慮到多種情況，亦或是連條件都可以自己編等，如例1具有一定的開放性，屬于一題多解；例3也具有開放性，需要學生分類討論.開放的問題設計有利于幫助學生發散思維，不受常規題的束縛，培養學生的創造力，強化學生的數學思維，提升課堂價值.

3.3 專題復習教學的關注點

一要關注學生的思維訓練.本節課的思維訓練包括已知直角三角形中兩個頂點坐標求另一個頂點坐標，要求解的頂點可能在坐標軸上，可能在對稱軸上，也可能在拋物線上.

二要關注學生的思路分析.本課例2介紹圓軌跡法的學生在講解時由直角三角形聯想到該點的軌跡是圓，十分巧妙，但在該學生敘述過程時，教師應關注學生思路是否清晰.筆者在磨課時發現有部分學生在闡述該過程時跳躍很快，學生回答結束，筆者會追問，學生說不出所以然，說明可能是對該相關知識點的學習是一知半解的.那么在復習課時教師發現學生薄弱知識點，應該對薄弱知識點加強鞏固.

三要關注滲透數學思想，例如本課中的數形結合、分類討論等.

四要關注課堂的主體.傳統課堂以教師講解、學生聽課為主，課堂中如果能采取不同的討論形式，如個人學習、同桌交流、小組學習、全班學習等，學生自然而然地成了學習的主人、課堂的主體，教師成為組織者和合作者.對于每道例題，教師可以引導學生自己提煉規律方法，縱觀整節課，鼓勵學生對整節課進行課堂小結.如本課中為了尋覓到垂直，先辨垂直判斷是否存在，再用垂直求出點的坐標，這樣就將三道例題串聯起來.

4 結語

專題復習課是教師們一直都在探究的問題，要想上好一節專題復習課雖然需要投入很多心思、時間，但對提高復習教學的成效有非常突出的優勢和作用，有利于學生對數學知識內在的構建和掌握.這就要求教師不斷提高鉆研解題的能力，不斷創新教學模式，教師應讓學生感受更多的數學魅力.

參考文獻：

［1］劉穎.例談初三數學專題復習課的設計——以“二次函數專題（一）”為例[J].上海中學數學，2017（09）：25-26+36.

［2］杜旭輝.探討初三數學復習中激活課堂教學的有效策略[J].讀寫算，2020（04）：166.

［3］于嬌.初三數學復習課專題課設計的研究[J].才智，2014（17）：165.

［4］張玉潔，周杰.優化初三數學復習課教學的實踐與思考[J].中國多媒體與網絡教學學報（下旬刊），2020（07）：212-213.