解讀符號學(xué)視角下的數(shù)學(xué)課堂交流

1 引言

近年來，符號學(xué)的觀點(diǎn)被廣泛應(yīng)用在各門學(xué)科，如電影、戲劇、醫(yī)學(xué)、建筑等，效果可觀. 在數(shù)學(xué)教育中，研究者們將不同的符號學(xué)的理論和視角整合到已有的心理學(xué)、人類學(xué)、語言學(xué)和社會學(xué)的理論中，以便分析和更好地理解數(shù)學(xué)的教與學(xué)的過程. Sáenz-Ludlow等認(rèn)為數(shù)學(xué)和數(shù)學(xué)的教學(xué)在本質(zhì)上都是符號實(shí)踐，其中，符號被發(fā)明、使用或再創(chuàng)造以使認(rèn)知操作或目的變得容易.^[１]

數(shù)學(xué)對象的非物質(zhì)的本性要求通過大量自然的表征（也就是，數(shù)學(xué)符號）來表達(dá)數(shù)學(xué)對象，以便它們能被社會地分享. 因此，學(xué)習(xí)數(shù)學(xué)既需要解釋數(shù)學(xué)符號，也需要通過和他人交流來建構(gòu)數(shù)學(xué)的意義. 這些解釋和意義不是當(dāng)場建構(gòu)的，而是從個(gè)人在不同的數(shù)學(xué)、社會和自然的情景下大量緊密相連的經(jīng)歷中產(chǎn)生并不斷發(fā)展的. 在這些經(jīng)歷中，多種符號系統(tǒng)（如語言、數(shù)學(xué)符號、手勢）結(jié)合起來，為一個(gè)不斷發(fā)展的數(shù)學(xué)意義的解釋打下了基礎(chǔ). Sáenz-Ludlow基于Charles Sanders Peirce的符號學(xué)理論建立了一個(gè)名為“解釋游戲”（interpreting game）的解釋性模型，說明了數(shù)學(xué)課堂中思考和交流的相互依賴性，以及教師和學(xué)生參與的關(guān)于符號的解釋.^[２]

2 從符號學(xué)視角分析數(shù)學(xué)課堂交流

數(shù)學(xué)交流需要自然語言、數(shù)學(xué)符號和其它符號系統(tǒng)中的手勢及肢體語言. 因此，課堂交流展示了一種符號學(xué)的本性，這已經(jīng)被數(shù)學(xué)家、數(shù)學(xué)教育者和心理學(xué)家直接或間接地承認(rèn). 任何個(gè)體的符號學(xué)活動(dòng)呈現(xiàn)了社會互動(dòng)的存在，但是關(guān)于社會互動(dòng)在思維過程中的角色是首位還是第二位的辯論依然存在. 從符號學(xué)的視角看，個(gè)體的認(rèn)知活動(dòng)和社會互動(dòng)都不是第一位的，它們以協(xié)作的方式共存，共同作用，以促進(jìn)符號解釋和產(chǎn)生意義的發(fā)展過程. 思考和交流（作為最廣泛意義上的社會互動(dòng)）是平行的，同時(shí)也是相互聯(lián)系的. Peirce的符號學(xué)理論，提出了獨(dú)特的原理來理解當(dāng)符號被解釋并轉(zhuǎn)換成新的符號時(shí)，思考和交流之間的相互依賴性. 在Peirce看來，思考、符號、交流和產(chǎn)生意義有著內(nèi)在的相互聯(lián)系. 個(gè)體和集體使用符號和解釋符號的過程，來源于社會互動(dòng)，產(chǎn)生的結(jié)果是個(gè)人意義的構(gòu)建. 這些個(gè)人意義將不斷地被修正和改進(jìn)，最終靠向圈內(nèi)人已建立的常規(guī)意義.

Peirce是這樣定義符號的，一方面它由對象決定，另一方面它又決定了人腦中的概念. Peirce稱后者為符號的“解釋項(xiàng)（interpretant）”，解釋項(xiàng)由對象間接決定，因此存在符號、對象及解釋項(xiàng)之間的三角關(guān)系. 符號給出了一個(gè)解釋項(xiàng)來表示對象，有著認(rèn)識論的功能，符號在它的對象和解釋項(xiàng)之間是不可少的.^[3]

此外，Peirce認(rèn)為符號不能稱之為符號，除非它被解釋或轉(zhuǎn)化為另一個(gè)更充分發(fā)展的符號. 在這種轉(zhuǎn)化中，符號被解釋成新的符號，隨之而來的是，更復(fù)雜的解釋項(xiàng)和對象出現(xiàn)在了解釋者的頭腦中，從廣義上來講，解釋項(xiàng)能被理解為一個(gè)符號向新的符號的轉(zhuǎn)化（見圖1）.

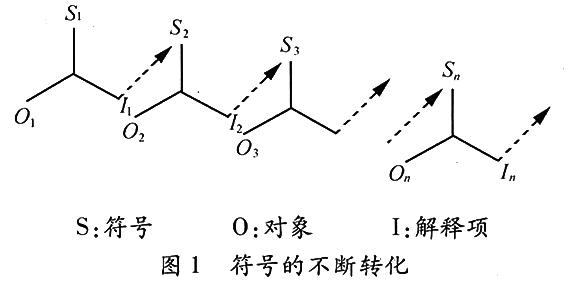
在符號向新的符號的不斷轉(zhuǎn)化中，伴隨的一系列解釋項(xiàng)逐漸形成了意義的產(chǎn)生. 這個(gè)轉(zhuǎn)化的過程本身是解釋的過程，通過這個(gè)過程，在符號施動(dòng)者的頭腦中符號逐漸被轉(zhuǎn)化成較少情景化而更為一般化的符號. Peirce考慮了不同種類、不同功能的解釋項(xiàng). 這里我們考慮的是有意圖的（intentional）、有效的（effectual）、交流的（communicational）和邏輯的（logical）解釋項(xiàng). 有意圖的解釋項(xiàng)是表達(dá)者頭腦中的定義，有效的解釋項(xiàng)是解釋者頭腦中的定義，有意圖的解釋項(xiàng)促使表達(dá)者（也就是意圖者）為發(fā)送信息而選擇符號，當(dāng)意圖者提出一個(gè)有意圖的解釋項(xiàng)，根據(jù)Peirce理論，解釋者進(jìn)行解釋并產(chǎn)生一個(gè)有效的解釋項(xiàng). 最后，交流解釋項(xiàng)是符號的意圖者和解釋者在交流中共同產(chǎn)生和分享的想法（即，達(dá)成的共識）. 其間有些解釋項(xiàng)提出了推斷和行為的計(jì)劃，稱之為邏輯解釋項(xiàng)，它對帶有他們自己的概念網(wǎng)的符號施動(dòng)者來說是有意義的，在隨后的交流計(jì)劃中這些邏輯解釋項(xiàng)進(jìn)一步接受更改和修正.

Rotman曾指出，交流對數(shù)學(xué)家的創(chuàng)造性活動(dòng)是必需的，因此交流對數(shù)學(xué)課堂中教師對學(xué)生的數(shù)學(xué)活動(dòng)也應(yīng)該是必需的.^[4]交流在本質(zhì)上是一個(gè)連續(xù)的符號解釋過程. 在這個(gè)過程中，教師和學(xué)生相互交換著他們作為意圖者和解釋者的角色，不斷構(gòu)建解釋項(xiàng)并轉(zhuǎn)化成新的符號（如，數(shù)學(xué)論據(jù)、圖表、口頭表達(dá)、手勢或任何其它可視符號），以解釋已確定的數(shù)學(xué)概念. 構(gòu)建解釋項(xiàng)意味著通過教師和學(xué)生主觀的解釋行為構(gòu)造數(shù)學(xué)意義，這些解釋行為決不是教師向?qū)W生過分簡單化的信息轉(zhuǎn)移.

師生之間的課堂交流要考慮到學(xué)生有意識并積極參與到解釋過程，Sáenz-Ludlow把這種課堂參與者共同建構(gòu)的解釋過程稱之為“解釋游戲”（以下簡稱IG）. 一開始，數(shù)學(xué)符號對教師來講可能是有意義的，但對學(xué)生來講它們就是簡單的毫無意義的書面記號. 通過IG，在學(xué)生的頭腦中產(chǎn)生了解釋項(xiàng)，給這些書面記號賦予了數(shù)學(xué)意義，即臨時(shí)的個(gè)人意義，接受修正和改進(jìn). 隨著IG的繼續(xù)，臨時(shí)意義越來越缺乏主觀性，書面記號逐漸成為數(shù)學(xué)符號，產(chǎn)生了交流解釋項(xiàng)，它們最終接近于數(shù)學(xué)概念的客觀的標(biāo)準(zhǔn)的意義（見圖2）.

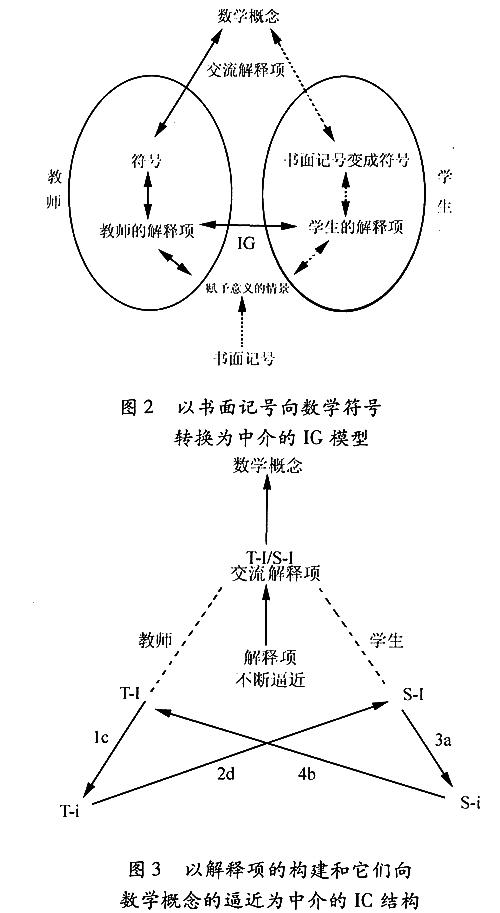
“解釋循環(huán)”（interpreting cycle，以下簡稱IC）是IG的基本分析單元. 每一個(gè)IC都是以某一類型意義的建構(gòu)為中介，為后續(xù)的循環(huán)做好準(zhǔn)備，而在后來的循環(huán)中又會出現(xiàn)新的意義，接受修正和進(jìn)一步的改進(jìn). 圖3表示了解釋循環(huán)的結(jié)構(gòu)，數(shù)字1、2、3、4顯示的箭向順序表示了由教師發(fā)起的一個(gè)循環(huán)的開始方向；字母a、b、c、d顯示的箭向順序則表示由學(xué)生發(fā)起的一個(gè)循環(huán)的開始方向. 每個(gè)IC是通過解釋、意圖、解釋項(xiàng)向新的符號的轉(zhuǎn)化，以及某種達(dá)成共識的數(shù)學(xué)意義或交流解釋項(xiàng)的最終出現(xiàn)組成的. 交流解釋項(xiàng)不斷進(jìn)化，最終接近數(shù)學(xué)概念.

考慮一個(gè)由教師發(fā)起的循環(huán)，在教師對一個(gè)數(shù)學(xué)符號的解釋行為中產(chǎn)生了一個(gè)有效的解釋項(xiàng)（T-I），T-I引發(fā)了一個(gè)有意圖的解釋項(xiàng)（T-i）. 教師表達(dá)了她的有意圖的解釋項(xiàng)（T-i），學(xué)生進(jìn)行解釋以便產(chǎn)生一個(gè)有效的解釋項(xiàng)（S-I）. 依次地，S-I引發(fā)了一個(gè)由學(xué)生表達(dá)的有意圖的解釋項(xiàng)（S-i），然后，教師解釋學(xué)生的S-i進(jìn)而產(chǎn)生了一個(gè)有效的解釋項(xiàng)（T-I），T-I又引發(fā)一個(gè)由教師表達(dá)的T-i. 學(xué)生解釋T-i，產(chǎn)生S-I，進(jìn)而引發(fā)一個(gè)由學(xué)生表達(dá)的S-i. 由于有效解釋項(xiàng)是存在于解釋者頭腦中的，我們只能通過表達(dá)出來的有意圖的解釋項(xiàng)來推斷其有效解釋項(xiàng). 因此，當(dāng)教師和學(xué)生在解釋過程中建構(gòu)和表達(dá)了有效的和有意圖的解釋項(xiàng)時(shí)（這可能產(chǎn)生邏輯解釋項(xiàng)，也可能不產(chǎn)生邏輯解釋項(xiàng)），IC一致繼續(xù)直到某種交流解釋項(xiàng)被表達(dá)出來.

課堂解釋游戲是基于Peirce的符號學(xué)理論建立的解釋模型，它把交流和社會活動(dòng)的社會的與個(gè)人的維度，以及意義產(chǎn)生過程的公共的與私人的維度聯(lián)系了起來，這樣就突出了數(shù)學(xué)意義的合作構(gòu)建過程. 解釋游戲成為了教和學(xué)的工具，同時(shí)也應(yīng)該變成提問的工具. 如何使學(xué)生參與解釋，參與到解釋游戲中，是數(shù)學(xué)教學(xué)面臨的主要挑戰(zhàn)之一. 為此，就有必要建立一種課堂環(huán)境，在這種環(huán)境下，師生之間的交流關(guān)系隨著直接的和間接的智力結(jié)果自然地出現(xiàn). 也就是，教師和學(xué)生應(yīng)該被平等地置于交流關(guān)系的建立中，在這其中，符號使用、符號解釋和提問變成了一個(gè)連續(xù)態(tài).

3 結(jié)束語

新課標(biāo)中強(qiáng)調(diào)，教學(xué)活動(dòng)是師生共同參與、交往互動(dòng)的過程，有效的數(shù)學(xué)教學(xué)活動(dòng)是教師教和學(xué)生學(xué)的統(tǒng)一.^[5]那么教師如何才能組織有效的課堂交流呢？為了把解釋游戲當(dāng)作教與學(xué)的工具，教師應(yīng)該認(rèn)真考慮她的教學(xué)活動(dòng)，這由兩部分組成──備課和實(shí)際的教學(xué)活動(dòng). 備課活動(dòng)應(yīng)該是建立在和學(xué)生不對稱的關(guān)系的基礎(chǔ)之上，教師反省她自己對數(shù)學(xué)概念的理解，準(zhǔn)備教學(xué)任務(wù)和教學(xué)策略以激發(fā)學(xué)生的好奇心. 在實(shí)際的教學(xué)活動(dòng)中. 教師（很大程度上）應(yīng)該維持與學(xué)生對稱的對話，不要忘記她的指引作用，但要將學(xué)生的思維轉(zhuǎn)換到她自己的思維范圍之內(nèi). 因此，教師有必要學(xué)習(xí)區(qū)分她的解釋項(xiàng)和她從學(xué)生的表述中推斷出來的解釋項(xiàng)，以便支撐和維持學(xué)生解釋項(xiàng)到更精確的符號的連續(xù)轉(zhuǎn)換.

成功的解釋游戲可以推動(dòng)符號使用、符號解釋，以及書面記號轉(zhuǎn)換成賦予較少主觀性（即，更為客觀）的數(shù)學(xué)意義的更成熟的符號. 在這些游戲中，教師和學(xué)生把他們自己作為有意識的解釋的主體，教和學(xué)成為互補(bǔ)的活動(dòng)，教師既教又學(xué)，學(xué)生既學(xué)又教，教師和學(xué)生在這個(gè)過程中都被授權(quán)教和學(xué)，形成一個(gè)活潑的互動(dòng).

參考文獻(xiàn)

[1] Sáenz-Ludlow, A & Presmeg , N. Semiotic perspectives on learning mathematics and communicating mathematically[J]. Educational Studies in Mathematics, 2006, 61: 1-10.

[2] Sáenz-Ludlow, A. Classroom interpreting games with an illustration[J]. Educational Studies in Mathematics, 2006, 61: 183-218.

[3] 涂紀(jì)亮編, 皮爾斯文選[M]. 涂紀(jì)亮, 周兆平譯. 北京：社會科學(xué)文獻(xiàn)出版社, 2006. 219-302.

[4] Rotman, B. Towards a semiotics of mathematics[J]. Semiotica, 1988, 72: 1-35.

[5] 中華人民共和國教育部. 全日制義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)[M]. 北京：人民教育出版社,2006.作者簡介 龐雅麗，女，1980年9月出生，山西孝義人，華東師范大學(xué)數(shù)學(xué)系2006級博士研究生，研究方向?yàn)閿?shù)學(xué)教育心理、中學(xué)數(shù)學(xué)教與學(xué)研究.