元認知理論在數學復習課中的運用

王 莉

美國兒童心理學家弗萊維爾指出：“元認知通常被廣泛地定義為任何以認知過程與結果為對象的知識，或是任何調節認知過程的認知活動，它之所以被稱為元認知，是因為其核心意義是對認知的認知。”可以說，元認知就是認知主體對自身心理狀態、能力、任務目標、認知策略等方面的認識。同時，元認知又是認知主體對自身各種認知活動的計劃、監控和調節。在復習課中運用元認知理論，能更有效地提高復習課的效率。

一、教師的“教”

1構建網絡，掌握規律

在復習課教學中，教師必須揭示教材中各部分知識的內在聯系，使學生從不同的角度加深理解，并通過比較以“求其異”、“求其同”，使學生掌握的知識系統化、深刻化，形成知識網絡，同時從不同的方面去激活學生思維的靈活性、獨創性和批判性，發展學生的元認知能力。為此，教師在教學中應采用“整體一部分一整體”的方法，重視學生正遷移能力的培養，防止負遷移的干擾。例如，中考中必考的現實背景的問題，一般是通過列方程或方程組、列不等式或不等式組、找函數關系二三種方法來解決。三種方法覆蓋了初中三年的教學，教師當然要指導學生詳細復習每一種方法，但更重要的是要提高學生在實戰中的判斷能力，使學生熟練地掌握規律，知道在什么情況下該用什么方法。這樣可以幫助學生提高對任務目標、認知策略的認識。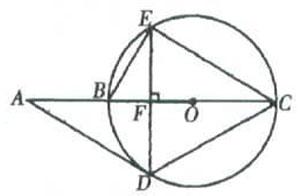

2展示思維，互相交流

講解例題有兩種方式。一是教師展示自己的思維過程，告訴學生解題時自己如何利用已知條件，遇到困難時如何做策略調整等，讓學生借鑒。

例題：如圖，已知AD是⊙O的切線，切點是D，直線AC經過圓心O，交⊙O于B、C兩點，弦DE⊥AC。垂足為F，∠A=30°。(1)求LBED的度數。

(2)ADCE是否是等邊三角形?請說明理由。

讀完題目，教師可以這樣說明自己的思路：“有切線的問題一般要連接圓心和切點，得∠ADO=90°。因為AA=30°，所以∠AOD=60°。要求LBED的度數，在這道有圓的題目中優先考慮圓周角，它等于所夾弧對的圓心角的一半，因此LBED=30°。第2問等邊三角形的判定方法常用的有兩個，我選擇……”即使是錯誤的思路也可展示，重要的是展示教師是如何將思路調整到正確的解題方向上的。

二是教師通過如“你是怎么想的?”“你為什么這樣想?”這些問題來引導學生展示自己的思維過程，讓學生互相交流、啟發，學會對問題解決的進程進行積極的、自覺的監控。

3組織反思，總結經驗

一節復習課不僅要讓學生重溫已學過的知識，還要使學生知道各知識點之間的聯系，一般的問題思考方法，老師、同學的方法是否能借鑒，自己的方法好在哪里，它能不能用于解決其它問題等。

如在上例講解完例題后，教師向學生提問：“解題時我們首先應該關注什么?”學生回答：“題目提到的已知量和未知量。”教師繼續提問：“本題涉及的量是什么?”學生回答：“與圓相關的線和角。”教師追問：“這些線與角是怎樣聯系在一起的?”學生會給出一系列定理，說出它們的關系。教師點出，這就是一般的解題思路。接下來請學生分析第2問兩種證法的優劣，與其他同學共同品評。由于學生問存在差異，因此在做課堂小結時，教師的點撥應循序漸進，兼顧先后，讓不同的學生在數學上有不同的發展。

學生的思維能力就在這樣的不斷探索和回顧反思中得到提高，學生的元認知能力因而也得到培養和開發。

二、學生的“學”

除在課堂上接受老師的引導之外，學生自己本身也應該有意識地掌握一些元認知方法。這里介紹美國數學家波利亞的自我提問法。這個方法以各個認識階段的一系列問題幫助學生進行自我觀察、自我監控、自我評價，不斷促進學生自我反省。

理解問題階段的問題：未知條件是什么?已知條件是什么?用已知條件足以求出未知量嗎?

擬定計劃階段的問題：過去見過這類題嗎?若見過，它是否以稍微不同的方式出現?我能用與未知條件相同或相似的熟悉問題的解法來解決這道題嗎?如果不能，我能從已知條件中找到(推導出)什么有用的東西?我是否用上了所有的條件和數據?

執行計劃階段的問題：能清楚地認定每一步都是對的嗎?能證明它是對的嗎?

回顧階段的問題：我能檢驗結果的正確性嗎?我能檢驗推理過程嗎?我能在其他問題上運用這個結果或方法嗎?

這個方法不妨印發給學生人手一份，讓學生做作業時先看看，配合課堂教學，加深印象。如上例的課后作業可布置兩道與例題相似(有與圓相關的線和角)的作業，再布置一道有特殊四邊形還有圓的題目。學生若遇上困難，可對照以上方法看哪些環節自己沒考慮周全，以加強自我意識，提高知識遷移能力。這樣做，學生綜合運用知識的能力會提高，心理素質也會提高，從而保障了學生在考試中的穩定發揮。

(責編王學軍)