運用數學知識學歷史

閆淑云

教學是一門科學，更是一門藝術，適當引入數學知識，既能使我們的歷史課堂內容豐富多彩，又增添了學生的學習興趣，使學生的知識達到融會貫通。

一、運用曲線圖進行直觀教學

例一：復習中國古代人口變化情況，如下圖。

有些歷史知識如人口變化、經濟發展情況等，分布在課本的各個章節，學生掌握起來比較困難。運用曲線圖教學，這些問題便會迎刃而解。

上課時先用多媒體投影出以下資料：縱觀數千年來中國人口的發展，我們不難發現，人口總量的增長是中國人口發展中最明顯的特征。

1.第一個坡，從夏朝至西漢末年（公元前21世紀到公元初），2000多年時間，中國人口增長沿著一條緩升的總量線波動，直至接近6000萬。

2.第二個坡，從東漢至明末（公元初到17世紀初）1600年左右的時間，中國人口增長圍繞著一條水平的總量線（6000萬至7000萬）上下波動。對于宋時期和明時期的人口總量，有學者認為已經達到或突破了1億。

3.第三個坡，從明末至清后期（17世紀初到1850年），大約200年時間，中國人口增長沿著一條向上傾斜的總量線波動，歷經1億、2億、3億，最終達到四億三千萬左右。

教師可以請兩名學生在黑板上繪出以上描述的大致曲線圖，鍛煉學生的繪圖能力。由學生自己發現問題，解決問題。教師要適時地提示、點評、總結。

①影響中國古代人口變化的因素有哪些？

②唐朝時人口增多，出現了人地矛盾，當時是如何解決的？帶來哪些影響？

③清朝人口猛增的原因主要是什么？

④上述情況對于我們今天制定人口政策有何指導意義？

例二：復習1840~1956年我國主要經濟成分。參考下圖。

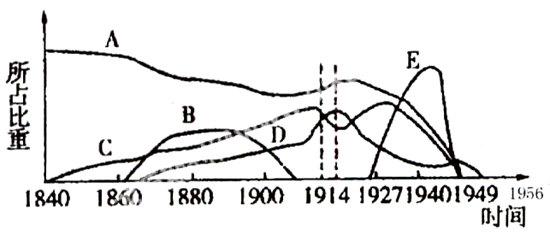
五種經濟成分：自然經濟、民族資本、外國資本、洋務資本與官僚資本。

教學方法同上例一。

畫曲線圖是歷史分析的一種方法。運用曲線圖教學直觀、一目了然，教師避免了枯燥乏味的填鴨式教學。我們在探究歷史問題的同時與數學知識實現了鏈接，學生想象力豐富，易于迸發出創造靈感，培養了學生發現問題、解決問題的能力，也令歷史課堂充滿生機和活力。

二、運用數學換算歷史年代，培養學生應用能力

近兩年高考常涉及干支紀年問題。怎樣將一些歷史紀年轉化為學生所熟識的公元紀年呢？這就需要數學知識了。

1.干支紀年。

公式：第一步：(公元年份-3)÷60得余數x；

第二步：x÷10所得余數對應天干；

第三步：x÷12的所得余數對應地支。

例如：公元2009年的干支紀年這樣計算：

（2009-3）÷60得余數x為26；

26÷10余數為6對應天干“已”；

26÷12余數為2對應地支為“丑”。

故2009年為已丑年。

2.公元換算成年號時，年號年數由“公元年數-年號元年+1”而得。如：641年文成公主入藏是貞觀幾年？

由“公元年數641-貞觀元年627+1”可得641年為貞觀15年。

年號換算成公元時，公元年數由“年號年數+年號元年-1”而得。如：民國24年是公元何年？由“民國年數24+民國元年1912-1”可得民國24年為公元1935年。

運用數學換算，學生把前人的認識轉化為自己的認識，進而又轉化為能力。

三、運用集合方法進行歷史教學

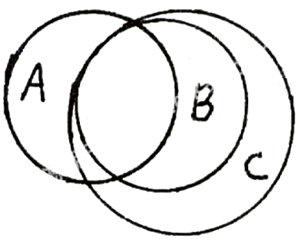
例一：復習近代史上的不平等條約《南京條約》及其附件(即A）、《望廈條約》(即B）和《黃埔條約》（即C）。這些條約單靠死記硬背不僅顯得枯燥乏味而且浪費時間。如何能讓學生輕松把條約內容記住、記牢是歷屆師生研討的重要課題。不妨運用集合方法試試。

先請兩名學生在黑板上繪出相應的集合圖，然后師生再共同探討、解決以下問題。

1.找出集合的交集部分：《南京條約》及其附件中除割地、賠款外的一切特權。

2.美國將門戶開放得更寬闊，體現在哪里？

3.法國又擴大了哪些侵略權益？

4.通過上述學習，你有何認識？

例二：復習史學著作《史記》(即A）、《漢書》(即B）、《資治通鑒》(即C）。方法同上。

在特定的教學情境中，集合方法能使學生精力集中，觀察細致，思維敏捷，識記速度加快，也大大減輕教師的負擔，獲取了更好的教學效果。總之，恰當運用數學知識，不僅有利于歷史的學習，同時在學習歷史的過程中，又能更好地理解和掌握數學知識。