“0.618”法、Fibonacci法、拋物線法搜尋復擺周期極值點

劉向遠,梅忠義,張穗萌

(1.皖西學院數理系,安徽六安237012;

2.合肥工業大學電子科學與應用物理學院,安徽合肥230009)

1 復擺模型

圖1所示的模型是一種鐘擺式復擺,當支點確定后,整個系統的質心可以隨圖中擺錘M的移動而變化.O點是整個裝置的支點,O點以上部分為菱形支架,O點以下為帶有刻度的直桿,其長度為L,桿上套有可移動的圓柱形擺錘M并以桿為對稱軸,其質量為m,半徑為R.通過調節擺錘M,當擺錘質心在B點距支點O為x0時,系統質心正好位于O點,此時,系統的轉動慣量為I0.

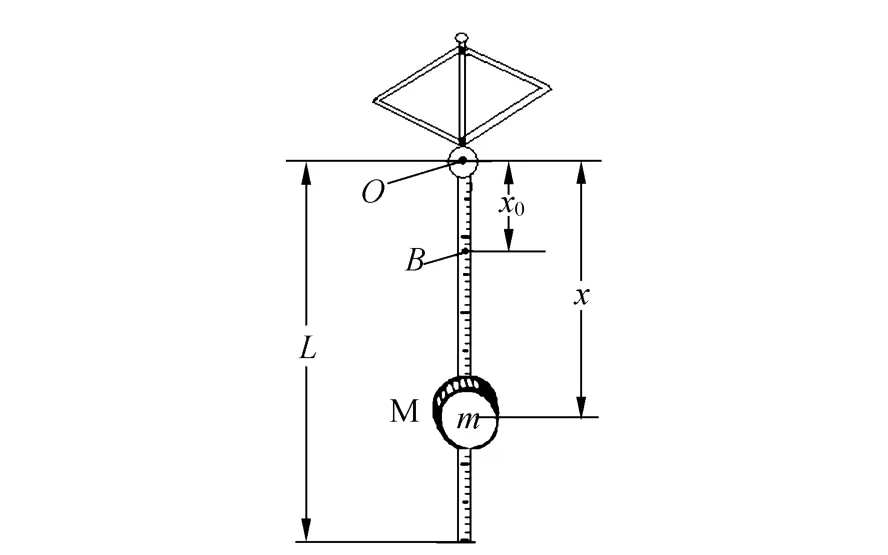
圖1 可變質心復擺模型

設擺錘質心在直桿上離開支點O的距離為x,當擺角小于5°時,復擺的周期公式為

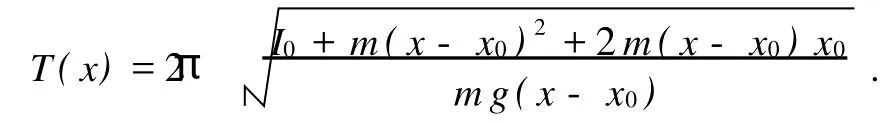
能夠證明T隨x在(x0,∞)區間內變化存在極小值[1-2].對于不同質量m的擺錘,T隨x變化的曲線如圖2所示.在實驗室條件下,如果未知此復擺的有關參數,要求快速、準確地尋找到它的極值點位置,可以采用一維精確搜索法來優選極值點.

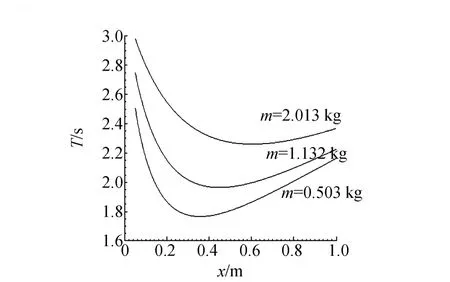
圖2 復擺周期T隨x變化的曲線

2 用“0.618”法、Fibonacci法、拋物線法搜尋復擺周期極值點的實驗方法

2.1 “0.618”法與Fibonacci法的基本思想

“0.618”法和Fibonacci法屬于一維精確搜索法中的分割法,這2種方法的基本思想是[3]:在已知的初始區間[a0,b0]內,選定兩個新的內點ak,bk,然后測出ak和bk對應的周期Tk和Tk′,并比較Tk與Tk′的大小,采取舍大取小的原則,舍去Tk與Tk′中對應的較大的內點以外的點,保留較小的內點,由此建立新的搜索區間,在新的搜索區間內再選取新的內點,重復以上的比較過程.按照這樣的步驟重復循環,逐步縮小搜索區間,直到達到所要求的區間范圍,并且取最后區間端點的平均值作為極小周期點的位置.

2.2 “0.618”法與Fibonacci法的不同點

“0.618”法與Fibonacci法在確定新的內點時有區別:“0.618”法確定新內點所取區分系數r=0.618,為恒定值.因此

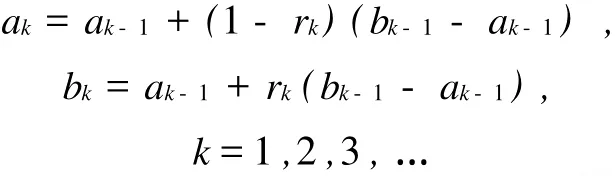
這樣,兩種方法在縮小搜索區間上有所不同,“0.618”法每次縮短搜索區間的長度為38.4%,而Fibonacci法縮短搜索區間的長度由1-rk來確定,是變化的.

另外,Fibonacci法中的區分系數還必須根據要求縮小的區間長度來確定Fn.假設要求將極值點xmin縮短到長度為l的區間內,則

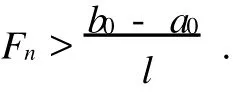
此時,取Fn在Fibonacci數列中滿足條件的最小整數,并由此確定n值[4].當區分系數為時,應該加上或減去很小的數值,本實驗減去0.02.

2.3 搜尋復擺極值點的拋物線法

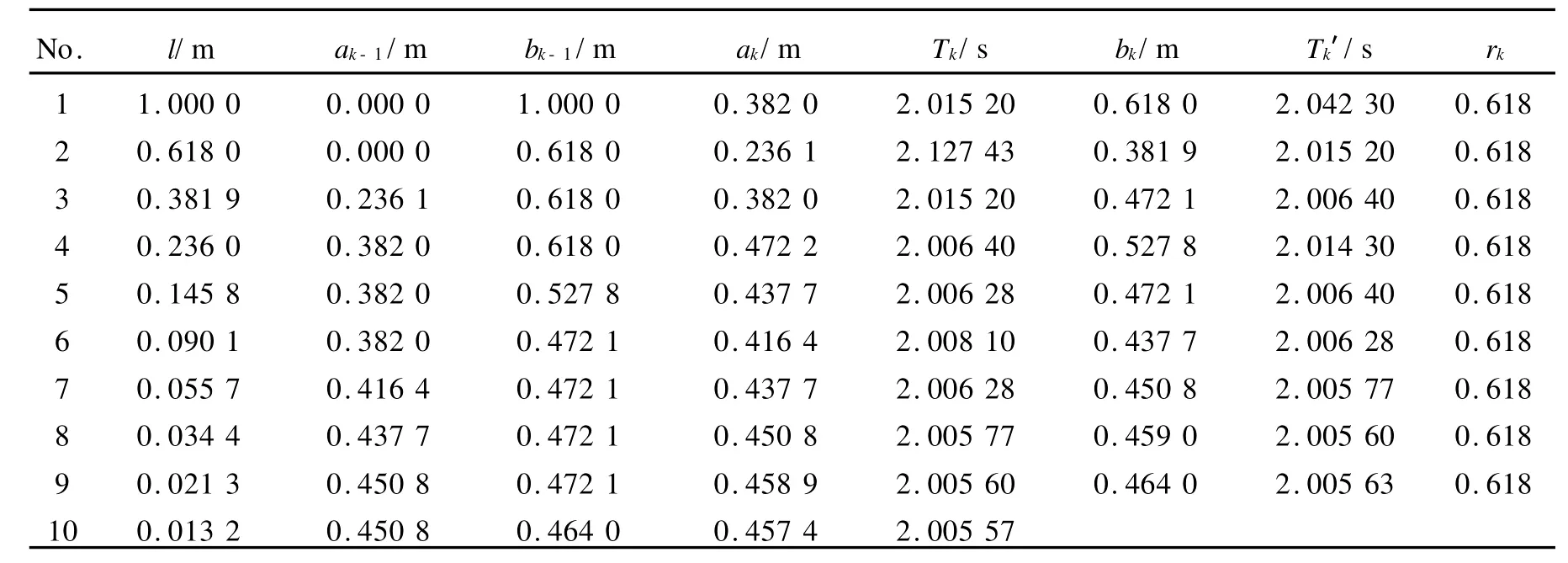
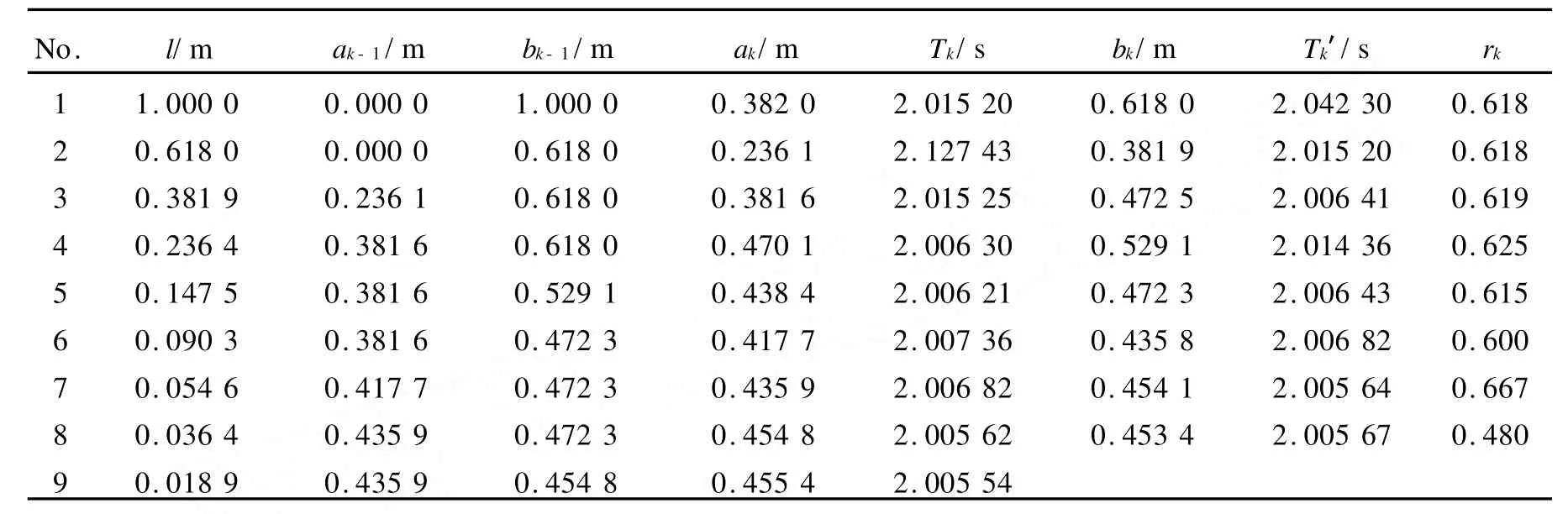
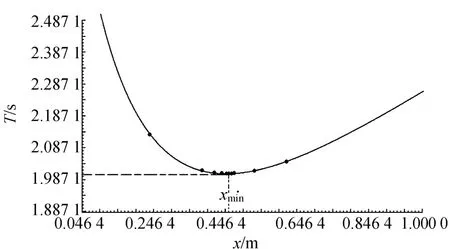
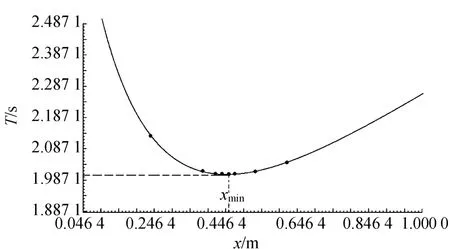
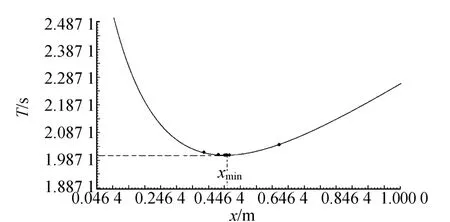
拋物線法又叫三點二次插值法,它是通過已知區間內的三點構造二次函數來逼近已知函數極小值的方法.如果要求將復擺的極小周期Tmin的位置xmin通過實驗的方法縮小到l范圍內,設L=b0-a0,則取復擺公式的初始區間[a0,b0]內三點x1

3 搜尋復擺周期極值點

下面采用計算機采集實驗數據[8],并結合復擺的T-x曲線來研究“0.618”法、Fibonacci法、拋物線法搜索復擺極值點的情況.

取復擺的初始區間[0,1],則區間長度L=1.000 0 m,要求將搜索區間縮小到可以接受的的范圍l≤0.020 m,則采用Fibonacci法時,得Fn>50,由Fibonacci數列知n=10,F10=55.表1為用“0.618”法測得的10組實驗數據,表2為Fibonacci法測得的9組實驗數據,表3為拋物線法測得的4組實驗數據.

圖3是根據表1,“0.618”法測得數據的9個區間端點在T-x曲線上的位置以及趨近于極值點的情況.圖中從左到右第6個點為極值點.此時復擺的極值點位置xmin=0.457 4 m,極小周期T=2.005 57 s.

圖4是根據表2,Fibonacci法測得數據的8個區間端點在T-x曲線上的位置以及趨近于極值點的情況.從圖中看,從左到右第5個點為極值點,其中第5和第6個點因實驗值相近,重疊在一起.此時復擺的極值點位置xmin=0.455 4 m,極小周期Tmin=2.005 54 s.

圖5是根據表3實驗數據,其中7個數據點在T-x曲線上趨近于復擺極值點的情況,從左至右,第5個點即為實驗測得的極值點,與第4個點靠得很近.此時,取Tmin=2.005 53 s,xmin==0.454 5 m.

表1 “0.618”法搜尋復擺極值點的實驗數據

表2 Fibonacci法搜尋復擺極值點的實驗數據

表3 拋物線法搜尋復擺極值點的實驗數據

圖3 “0.618”法搜索復擺極值點的情況

圖4 Fibonacci法搜索復擺極值點的情況

由以上結果可以看出:

1)以上實驗中,按實驗要求,“0.618”法用了15次測量(不包括重復數據點),Fibonacci法用了17次測量.由于在“0.618”法的內點中出現了較多的重復數據,使得“0.618”法比Fibonacci法的測量次數較少.由此可見,盡管從理論上講Fi-犫狅狀犪犮犮犻法比“0.618”法收斂速度快,但是由于受到實驗條件的影響,實際情況并非如此.

圖5 拋物線法搜尋復擺極值點的情況

2)Fibonacci法搜索復擺極值點比“0.618”法精度高.以上實驗中,這2種方法都通過第8組數據比較后,即8次搜索后,Fibonacci法將搜索區間長度縮小到0.018 9 m,而“0.618”法將搜索區間長度縮小到0.021 3 m.因此,采用實驗的方法搜尋復擺的極值點,從搜索精度來看,Fibonacci法比“0.618”法較高,但從搜尋速度上看Fibonacci法并非占優勢.

3)拋物線法搜尋復擺極值點比“0.618”法和Fibonacci法速度較快且精度較高.從以上實驗數據可以看出,拋物線法經過7次測量和4組數據的比較就可以將最小周期點位置縮小到l=0.015 5 m范圍內.

4 結束語

“0.618”法、Fibonacci法和拋物線法都屬于最優化方法中的一維精確搜索法,在實驗中將這些方法應用于物理學中復擺的極值點搜尋,拋物線法較“0.618”法和Fibonacci法效果好,測量次數少,而且精度較高;使用Fibonacci法較“0.618”法在搜尋精度上有較好的提高,但是在搜尋速度上并不占優勢.不僅如此,還可以用這些方法搜尋物理學中其他單值單峰的極值點問題,在具體應用這些方法時適當地應用它們的優點,有利于得到需要的實驗結果.

[1] 肖蘇,任紅.實驗物理教程[M].合肥:中國科技大學出版社,2000:149-153.

[2] 毛瑞全,劉翠紅,鄭卿.復擺方程的一種求解方法[J].物理實驗,2008,28(3):45-46.

[3] 佘守憲,胡頡.黃金數與Fibonacci數列[J].物理與工程,2006,16(2):6-8.

[4] Fink D,John H.Mathews and Kurtis.數值方法[M].周璐,陳渝,錢方,譯.北京:電子工業出版社,2005:319-321.

[5] 袁亞湘,孫文瑜.最優化原理與方法[M].北京:科學出版社,2001:84-89.

[6] 薛毅.最優化原理與方法[M].北京:北京工業大學出版社,2004:153-155.

[7] 解可新,韓立興,林友聯.最優化方法[M].天津:天津大學出版社,2002:22-24.

[8] 梅忠義,倪菱湖,劉向遠.黃金分割法在物理實驗中的應用[J].大學物理實驗,2006,19(2):51-52.