基于多結構元素的脊骨邊緣提取
孫晶瑩,王佩宇
(1.長春工程學院 理學院,吉林 長春 130012;2.國家開發銀行,北京 100037)
0 引言
圖像的邊緣對人類的視覺系統具有重要意義,它是人類判別物體的重要依據,是圖像的最基本特征之一。邊緣中包含著景物有價值的邊界信息,這些信息可以用于圖像分析、目標識別以及圖像濾波,并且通過邊緣檢測可以極大的降低后繼圖像分析處理的數據量。所謂邊緣是指其周圍像素灰度有變化的那些像素的集合。邊緣廣泛存在于物體與背景之間,物體與物體之間。物體的邊緣是由灰度不連續所反映的。圖像邊緣檢測是圖像處理中的一項關鍵技術,邊緣檢測的實質是采用某種算法來提取出圖像中對象與背景間的交界線。
圖像邊緣檢測對于物體識別是非常重要的,得到圖像的邊緣,能使圖像分析大大簡化。很多圖像并沒有具體的物體,對于這些圖像的理解取決于它們的紋理性質,而提取這些紋理性質與邊緣檢測有極其密切的關系。所以邊緣檢測是數字圖像分析處理的前提,檢測結果的優劣影響著下一步圖像壓縮、計算機視覺、模式識別的應用,所以對它的研究具有現實意義和理論意義。
運用數學形態學的基本理論和方法,從結構元素的角度出發,提出了—種多結構元素的選取方案,并采用適當的處理算法進行圖像的邊界識別,進而達到脊骨圖像中邊緣信息提取的目的。
1 數學形態學原理
數學形態學是一門建立在嚴格數學理論基礎之上的學科,它的理論基礎涉及到微分幾何,拓撲學,現代概率論,近世代數與集論,圖論等一系列數學分支。另一方面,數學形態學又是一門密切結合實際的學科,它在數字圖像處理中有廣泛的應用。
數學形態學作為一種用于數字圖像處理和識別的新理論和新方法,它的理論很復雜,是“驚人的數學”,但它的基本觀念卻是簡單的和優美的。它最基本的思想是將圖像看成是點的集合,用結構元素對其進行移位、交、并等集合運算從而構成了形態學的各種處理算法,作為一種特殊的的數字圖像處理方法,數學形態學有其獨有的特性。
1.1 二值形態學
數學形態學在二值圖像處理中有四種基本變換,包括膨脹、腐蝕、開變換和閉變換。它們是全部形態變換的基礎。設A是被研究的圖像,B是結構元素,則A被B膨脹的結果可以定義為其中符號Y是集合論中的“并”的記號。A⊕B又稱為A與B的Minkowski和。
腐蝕的定義是通過膨脹以及圖像反射和集合取補的概念來定義。A被B腐蝕的結果為A?B=(Ac⊕c,其中Ac表示A的補或余集,即從整幅圖像中去掉A后所剩的部分。上式表明,先求A的補集被B的反射膨脹的結果,再求這一結果的補,最終得到的圖像便稱為A被B腐蝕的結果,或A與B的Minkowski差。
A被B進行開運算的結果,或者簡稱為A對B的開,定義為A?B=(A?B)⊕B,即A先被B腐蝕,再被B膨脹的結果。利用開運算可以消除散點和“毛刺”部分。即對圖像進行平滑。對于標準零件,可以通過檢驗毛刺部分的大小來判斷它是否合格。
圖像A被結構元素B進行閉運算后的結果,或A對B的閉,定義為:A·B(A⊕B)?B。因此,執行閉運算的過程與開運算恰好相反:先被B膨脹,再被B腐蝕。
1.2 灰度形態學
實際應用中絕大多數遇到的是灰值圖像,如遙感圖像,顯微圖像,照片等。為此,我們引入灰值圖的圖像代數運算。
定義2.1 設h和k分別為定義在E的子集H和K上的函數,則h被k膨脹后依然是一個函數,記為h⊕k,它由下式定義:
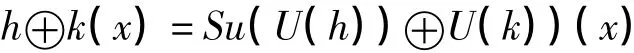
定義2.1 設H和K都是E的子集,且有函數h:H→G,k:K→G,h被k腐蝕仍為函數,記為h?k,它按下式定義:
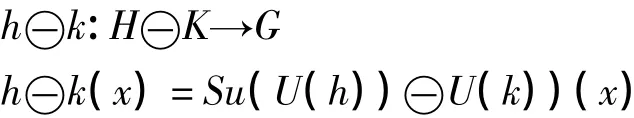
按照定義,計算h?k時要先計算h和k的陰影U(h)和U(k),再計算U(h)和U(k)在二值意義下的腐蝕運算,最后再計算這一結果的表面函數。
與二值圖的開變換與閉變換相似,可以用灰值圖的腐蝕與膨脹定義灰度圖的開變換與閉變換。設函數h,k的定義域都是E的子集,h被k開變換定義為h?k=(h?k)⊕k,
h被k閉變換定義為h?k=(h⊕k)?k
2 多結構元素提取邊緣流程
實驗數據是一幅脊骨圖像,具體提取過程如下:
(1)預處理。首先對原始影像作基于色彩空間的變換,并提取表示亮度信息的波段。然后根據影像灰度直方圖對圖像進行閾值分割,幅值小于閾值的系數為噪聲,給予抑制,而幅值大于閾值的系數給予一定的增益。經過如此處理后,達到了增強圖像的目的。結果如圖1所示。
(2)多結構運算。大尺度的結構元素有利于去噪和圖像中景物輪廓的定位,而小尺度的結構元素有利于保持景物中的小細節,這一步中,結構元素大小的選取決定了脊骨信息的提取尺度。因此先用尺寸較小的矩形結構元素進行膨脹,再使用尺寸較小的圓形結構元素進行開運算,以保持圖像中的細節。形態學開運算后,依據脊骨圖像自身的幾何特征,使用長線狀結構元素進一步對形態學膨脹后的結果進行形態腐蝕運算得到脊骨圖像邊緣,如圖2所示。
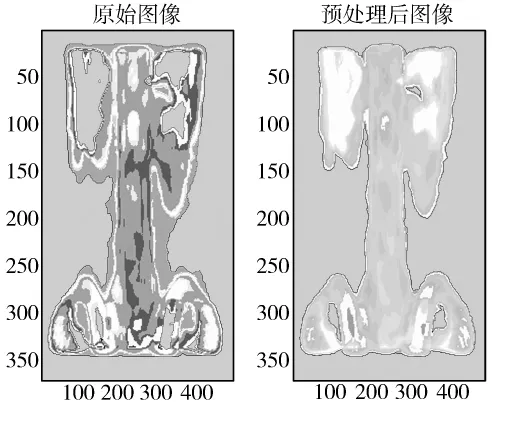
圖1

圖2
(3)常用邊緣算子檢測。選用sobel,canny兩個常用的邊緣檢測算子對脊骨圖像進行邊緣檢測,如圖3所示。其中(a)為原圖,(b),(c)分別為sobel,canny算子檢測結果。
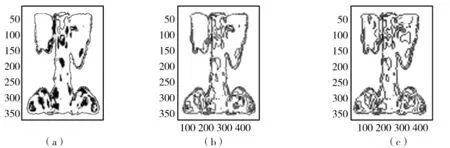
圖3
(4)抗噪性。加入椒鹽噪聲,對圖2,圖3進行抗噪性實驗,實驗結果如圖4所示。其中圖(a),(b),(c)分別為sobel,canny算子和多結構元素抗噪性檢測結果。

圖4
3 實驗結果分析
從圖中可以看出,用常用的邊緣算子提取輪廓包含了很多不重要細節,邊緣不連續情況較嚴重且存在誤檢,且算子抗噪性較差。而用多結構元素的算法檢測邊緣,在一定程度上保持圖像邊緣細節,邊緣的連續性及抗干擾能力方面都有所增強。
該算法的優勢:用多結構元素的方法可以提取不同大小的邊緣,有利于提取細節信息和保持圖像整體邊緣輪廓,在一定程度上保證了圖像信息的完整性,對噪聲的圖像處理的比較好,對噪聲有一定的抑制能力,該方法具有通用性,有較好的適用價值。此外,如何采用恰當的結構元素組合,建立對不同類型的圖像進行針對性邊緣提取的客觀評價算法,這一點既是難點也是一個很有價值的研究方向,有待進一步研究。
[1]Liang Yong.Applications of multi-orientation morphological structure elements in edge detection[J].J Yunnan University,1999,21(25):392 -394.
[2]岳洪偉,李揚,蔡肯.數學形態學在圖像處理中的應用與展望[J].影像技術,2006(2):19-21.
[3]魏明果.實用小波分析[M].北京:北京理工大學出版社,2005.
[4]唐常青,呂宏伯,黃錚,等.數學形態學方法及其應用[M].北京:科學出版社,2005.
[5]賀興華,周媛媛,王繼陽,等.MATLAB7.X圖像處理[M].北京:人民郵電出版社,2006.
[6]任獲榮.數學形態學及其應用[D].西安:西安電子科技大學,2004.
[7]龔煒,石青云,程德民.數字空間中的數學形態學一理論及應用[M].北京:科學出版社,1997.

