多個供應商供貨時供應商最優生產能力的設置

鄭士源

（上海海事大學 交通運輸學院，上海 200135）

0 引言

供應鏈合作伙伴的信息共享是指在供應鏈環境下，合作企業間關于供應鏈運行的各種信息能夠從一個企業，開放地、有效地、自動地流向另一個企業，即整個供應鏈上的企業可以分享信息資源。供應鏈合作伙伴之間加強信息的共享，可以降低企業中成員獲取信息的成本，提高信息運用的效率，進而提高整個供應鏈企業對市場的響應速度與質量。但供應鏈信息共享存在很多障礙，掌握較多信息的企業在與其他企業合作時會故意曲解信息來掩蓋他們的意圖，最終導致雙方收益都受影響。因此如何通過適當的激勵機制來實現供應鏈信息的共享一直是供應鏈管理的熱點問題。本文將運用機制設計中的共同代理方法，研究由多個供應商和一個制造商所組成的供應鏈中，如何通過恰當的合同安排來實現供應商和制造商之間關于需求信息的共享，從而實現整個供應鏈效率的最優化。

1 模型

1.1 問題描述

本文討論由供應商和制造商組成的兩級供應鏈系統。在此供應鏈系統中，制造商對于市場信息有著更為準確的預計，對市場的需求預測由三部分構成：市場需求的均值（μ），制造商利用其私人信息作的預測（ξ），市場需求預測的誤差（ε）。上述變量中，μ為供應商和制造商的共同信息，因此對他們而言都是確定性變量；ξ是制造商的私人信息，對于制造商而言是確定性變量，對于供應商而言是隨機變量；市場需求預測的誤差ε對于供應商與制造商而言均為隨機變量。由兩個供應商向制造商同時供貨，任何一個供應商均在他生產能力的許可范圍內盡可能滿足制造商的訂購要求，當然他的生產能力可能超過制造商的訂購要求，也可能不能滿足制造商的訂購要求。供應商和制造商間的合同形式為其中為制造商向各個供應商的支付。兩個供應商與制造商的博弈順序如下：①制造商向各個供應商提供其私人信息當然可以等于ξ，也可以不等于ξ；②各個供應商根據ξ^i決定生產能力ki制造商向各個供應商支付；③制造商決定其向每個供應商的訂購量，各個供應商在他生產能力的許可范圍內盡可能滿足制造商的訂購要求。

本文各模型中的變量和參數含義見表1。

1.2 基本假設

（1）ξ，ξ1，ξ2它們的分布函數和密度函數滿足單調似然率條件，即且分布函數和密度函數是共同知識；

（2）ε 的密度函數為非遞減函數，即 g'(ε)≥0；

（3）供應商1和供應商2生產產品的邊際成本和設置生產能力的邊際成本均相等，即c1=c2=c，ck1=ck2=ck；

（4）各種情況下供應商1和供應商2對制造商的批發價相同且不變，即w1=w2=w。

1.3 模型建立

根據問題的描述，供應商 1和 2的利潤如（1）、（2）式所示，制造商的利潤如（3）式所示。

表1 變量和參數表

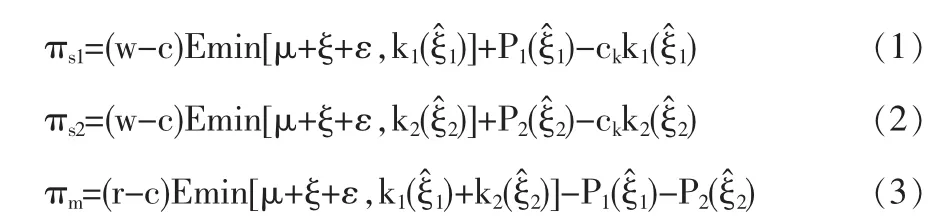
考慮供應商1，其面臨式（4）～（6）構成的優化問題。

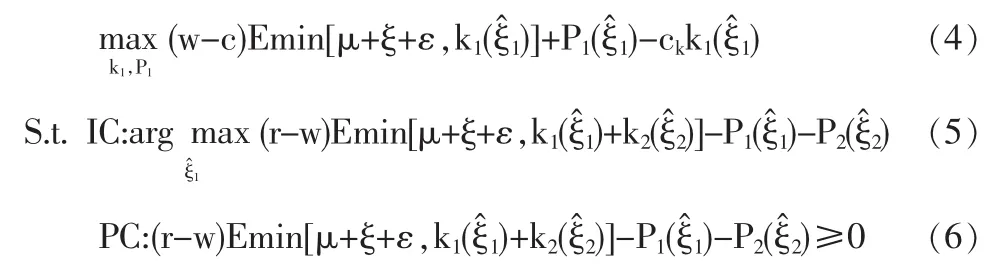
上述優化問題的約束條件中：IC（Incentive Compatibility）為激勵相容條件，即制造商選擇使自己利潤最大的信息ξ^1向供應商1匯報；PC（Participation Constraint）為個人理性條件，即制造商的利潤必須大于等于保留利潤0。

2 模型分析

2.1 模型求解

求解上述優化問題，得到如下命題。

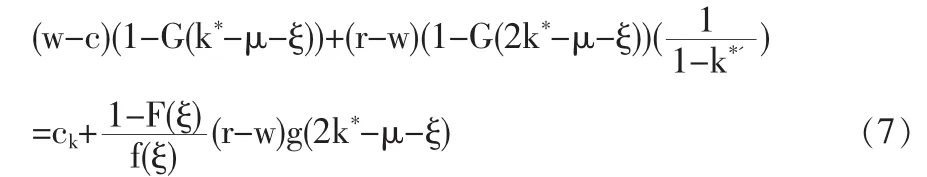
其中：k*'=dk*/dξ。

2.2 敏感性分析

2.2.1 ck、c和 μ 的影響

2.2.2 需求不確定的影響

由于無法從（7）式求得k*的解析解，因此本文通過數值模擬來分析需求不確定對供應商最優生產能力設置的影響。取 r=20，w=10，c=7，ck=2，μ=12，ξ服從 0 到 10 的均勻分布，而ε服從均值為0、標準差為σε的正態分布。計算不同σε下兩個供應商的最優生產能力的總和，結果如表2所示。

由表2可得如下命題。

命題3 隨著需求不確定的增加，供應商的最優生產能力設置呈下降趨勢。

從上述命題可以看出：隨著需求不確定的增加，市場風險加大，供應商的決策趨于保守。

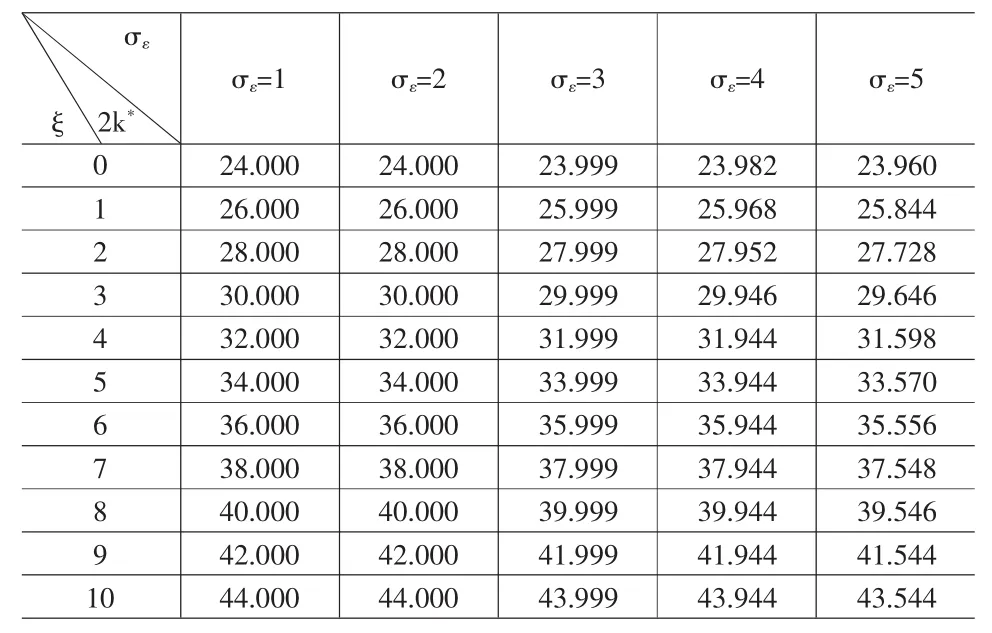
表2 需求不確定對供應商最優生產能力設置的影響

2.3 與單個供應商供貨相比較

單個供應商供貨時供應商面臨式（8）～（10）構成的優化問題。求解該優化問題可得此時供應商最優生產能力的一階條件如（11）式所示（證明見 Ozer和 Wei，2006）。

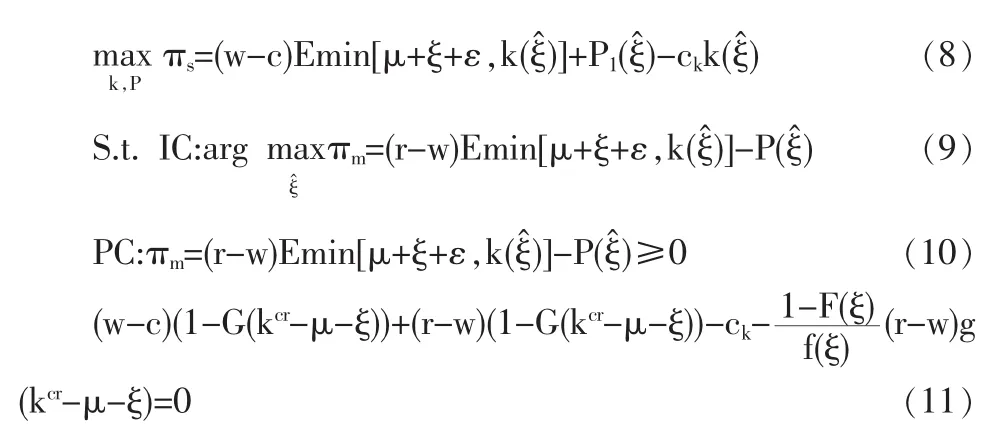
比較單個供應商供貨和兩個供應商供貨時供應商的最優生產能力配置和對制造商的影響，可得如下命題。

命題4 兩個供應商供貨時最優生產能力的設置大于單個供應商供貨時的最優生產能力配置，即kcr≤2k*（證明略）。

命題5 兩個供應商供貨時制造商的利潤大于一個供應商供貨時制造商的利潤，即（證明略）。

供應鏈的無效可能由下列因素導致：需求的不確定、供應商和制造商信息的不對稱以及供應商和制造商的壟斷地位。而供應商和制造商的壟斷通常造成 “雙重加價（Double Marginalization）”的現象。這三個因素共同導致了在一個供應商供貨的情況下，供應商生產能力的設置低于整個供應鏈的最優生產能力，進而影響了整個供應鏈的總體利潤（Ozer和Wei，2006）。在上述三個因素中，需求的不確定和信息的不對稱相對于供應鏈系統來說是外生變量，是供應商和制造商所無法控制的，而只有增加供應商的數量，將供貨任務分配給多個供應商才是制造商所能決定的。因此即使在單個供應商可以滿足制造商要求的情況下仍然向多個供應商進行采購。這是打破供應商的壟斷地位，提高整個供應鏈利潤的有效途徑。

2.4 與系統最優相比較

當供應商或制造商采用縱向一體化戰略時，整個供應鏈的效率達到最優狀態，此時整個供應鏈的利潤如（12）式所示，由此可得供應商最優生產能力設置的一階條件如（13）式所示（證明見 Ozer和 Wei，2006）。

同樣采用數值模擬的方法對兩個供應商供貨時供應商的生產能力設置及整個供應鏈的利潤與供應鏈系統的最優狀況進行比較，各參數的選取同2.2.2。結果見表3和表4。

由表3和表4可得如下命題：

命題6 隨著需求不確定的增加，兩個供應商最優生產能力總和同系統最優生產能力之間的差距減小，此時整個供應鏈的總利潤與供應鏈系統最優利潤間的差距也減少。

由上述命題可見，盡管兩個供應商供貨可以解決單個供應商時因供應商和制造商的“雙重加價”造成的供應商生產能力不足的缺陷，但同時也會造成生產能力的“過度設置”。而隨著市場風險的增加（需求不確定的增加），供應商的決策趨于保守，卻使得上述“過度設置”的現象得到一定程度的緩解，進而有利于整個供應鏈系統效率的提高。而在單個供應商供貨時，市場風險的增加使得供應商的生產能力與系統最優之間的差距呈不斷增加的趨勢（Ozer和Wei，2006）。這與兩個供應商供貨時的情形恰好相反。可見，當市場存在較高風險的時候，增加供應商的數量有利于整個供應鏈系統效率的提高。

3 供應鏈系統的優化

為解決兩個供應商供貨時供應商生產能力的 “過度設置”，必須改變供應商與制造商之間的合同機制，而命題7則提供了這樣一種在兩個供應商供貨情況下可以達到系統最優的合同機制。

命題7 當供應商1或2最優生產能力滿足由（8）所示的微分方程時，兩個供應商最優生產能力總和可使整個供應鏈的利潤達到最優，即（證明略）。

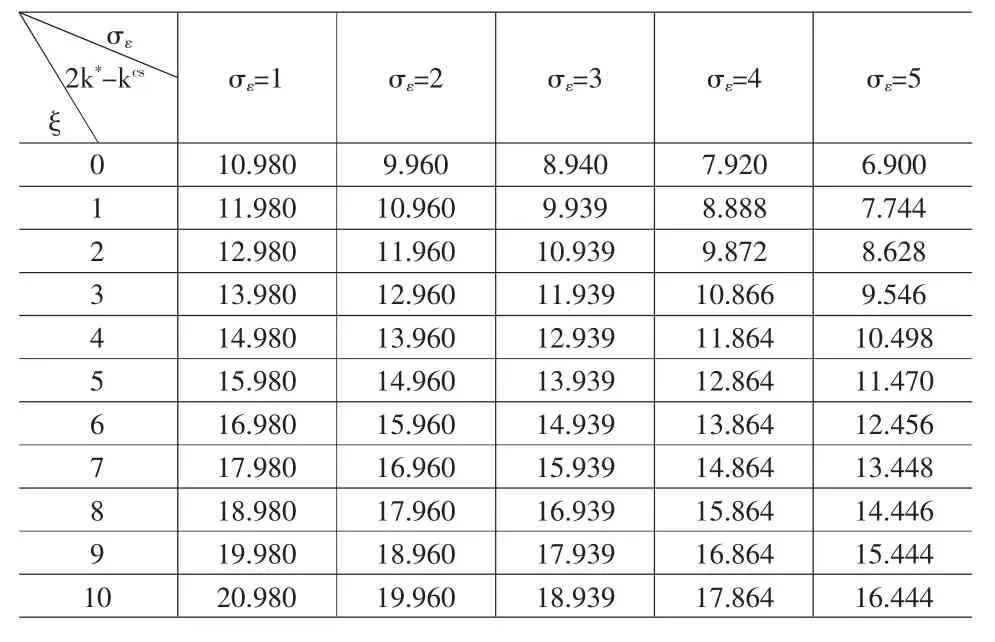
表3 需求不確定對兩個供應商最優生產能力總和同系統最優生產能力之間的差距的影響

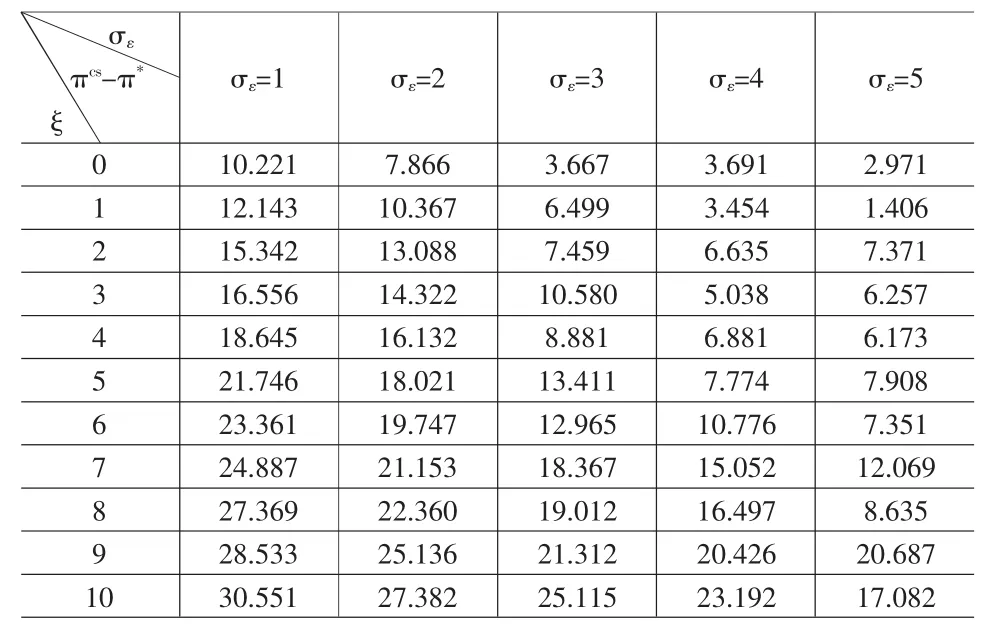
表4 需求不確定對兩個供應商供貨時供應鏈總利潤同系統最優利潤的差距的影響

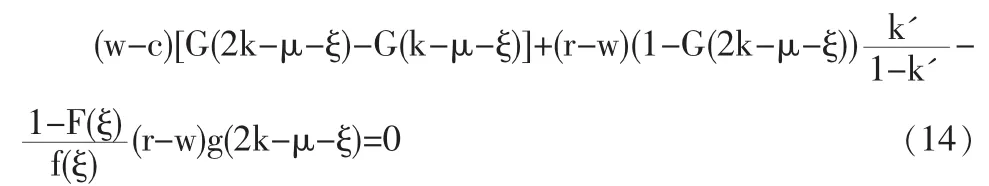
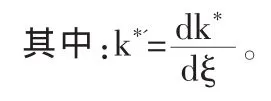
當單個供應商供貨時，一般的非線性生產能力設置合同不能使供應鏈系統的效率達到最優，因而必須采用更為復雜的合同形式（Ozer和Wei，2006）。而兩個供應商供貨時，上述一般的非線性生產能力設置合同卻可以做到這一點。因此從簡化機制，提高供應鏈效率的角度出發，可考慮增加供應商的數量，簡化供應合同。

4 結論與展望

本文從供應商的角度出發，考慮需求信息不對稱情況下多個供應商供貨時供應商最優生產能力設置的決策，指出此時供應商最優生產能力隨其成本和市場需求的不確定性的增加而減少，隨市場需求均值的增加而增加。通過與單一供應商供貨相比較得知，多個供應商供貨時供應商的最優生產能力和制造商的利潤較單個供應商供貨時高。而與供應鏈系統的最優狀態相比，多個供應商供貨可能會造成供應商“過度”設置生產能力；隨著需求不確定的增加，其與系統最優生產能力之間的差距減小，整個供應鏈的總利潤與供應鏈系統最優利潤間的差距也減少，整個供應鏈系統的效率有所提高。此外，本文給出了兩個供應商供貨時可達到供應鏈系統最優狀態的合同機制，指出從增加制造商和供應鏈的整體利潤的角度出發，即使在單個供應商可以滿足制造商要求的情況下仍然應向多個供應商進行采購。

對于本文的模型還可作更多的拓展，比如當供應商的數量趨于無窮大對供應鏈的影響；供應商之間的合謀對供應鏈的影響；供應商向制造商提供多種產品時最優生產能力的設置；制造商數量增加時供應商最優生產能力的設置等。這些都是需進一步研究的問題。

[1]Tayur S.Quantitative Methods for Supply Chain Management[M].Dordrecht：Kluwer Academic Publishers,1999.

[2]Aviv Y.The Effective of Collaborative Forecasting on Supply Chain Performance[J].Management Science,2001,47(10).

[3]Aviv Y.On the Benefit of Collaborative Forecasting Partnership between Retailers and Manufactures[J].Management Science,2007,53(5).

[4]馬新安，張列平，馮蕓.向多個供應商采購的存貯模型研究[J].應用數學與計算機數學學報,2000,14(2).

[5]劉東平.需求隨機情況下向多個供應商采購的期望值模型研究[J].科學技術與工程,2005,5(5).

[6]王紅衛，馬新安.大型工程物資供應組織中的合作伙伴選擇[J].計算機集成制造系統—CIMS,2001,7(7).

[7]王高雄，周之銘，朱思銘，王壽松.常微分方程[M].北京：高等教育出版社，1983.