基于最小二乘SVM的商業銀行經營的績效評價
李文博
(浙江師范大學 工商管理學院,浙江 金華 321004)
1 評價指標體系構建
商業銀行經營績效評價是一個復雜的系統,是銀行內部因素與外部環境相互聯系、交互作用的綜合結果。指標體系是經營績效評價內容的載體,也是評價內容的外在表現。商業銀行經營績效評價指標必須充分體現經營績效的基本內容,圍繞經營績效的因素結構,建立邏輯嚴密、相互聯系、互為補充,又相互獨立的評價指標體系。根據指標體系建立的目的性、科學性、全面性、相對性、通用性、動態與靜態相結合、定量與定性相結合等原則,按照系統的思想對經營績效的組成部分加以分解,將這些組成部分(或稱為要素)整理成一種遞階層次的順序,分別對組成部分進行評價,再對整個經營績效系統進行評價。
經營績效評價實際上是一個數據泛化擬合問題,即先根據輸入和輸出樣本進行學習,然后對不在學習樣本集中的輸入數據,計算出相應的輸出值。模型的輸出即為經營績效綜合評價值,模型的輸入即影響經營績效的各種可觀測指標。在借鑒現有文獻的基礎上,本文提出如下評價指標體系,如表1。

表1 商業銀行經營績效評價指標體系
在實際應用中,由于所選用的指標量綱不是統一的,需要對指標的數據進行變換處理,消除正、逆指標的影響,得到標準化數據。
對正指標:Xij=(Xij-min{Xij})/(max{Xij}-min{Xij})
對逆指標:Xij=(max{Xij}-Xij)/(max{Xij}-min{Xij})
上式中,Xij為i銀行的j指標的數值。
2 最小二乘SVM基本原理描述
支持向量機回歸有ε—支持向量機回歸、υ—支持向量機回歸和最小二乘支持向量機回歸等。最小二乘SVM回歸是Suykens J.A.K在1999年提出的最小二乘SVM在回歸估計中的應用,不同于前兩種算法,最小二乘SVM采用二次損失函數,并把優化問題轉化成解線性方程問題而非二次規劃問題,約束條件也變為等式約束而非不等式約束。雖然最小二乘SVM沒有標準的SVM具有的較高準確率且能保證所得解是全局最優解的特點,但由于它求解的是線性方程問題,當數據量較大時,具有所需計算資源較少、求解較快和收斂速度更快的優點。SVM方法的基本思想可概括為:由于大多數情況樣本點呈非線性關系,因此,將每一個樣本點用一個非線性函數φ(x)映射到高維特征空間,再在高維特征空間進行線性回歸,從而取得在原空間非線性回歸的效果。對其算法作如下描述:
Step2.相關參數及核函數的確定
在SVM中,根據Hilbert-Schmidt原理,任何滿足Mercer條件的函數都可以作為核函數K(xi,xj),常用的核函數K(xi,xj)一般有如下四種:線性函數(Linear Function):k(x,x/)=xTx/;多項式函數(Polynomial Function):k(x,x/)=(γxTx/+r),γ>0;徑向基函數(Radial Basis Function):k(x,x/)=exp(-γ||x-x/||2),γ>0;Sigmoid 函數:k(x,x/)=tanh(γxTx/+r),γ>0,其中,γ,r,d 為核函數的參數。
核函數的值等于向量x1,x2在特征空間φ的內積,即K(x,x/)=φ(xi)*φ(xj),使用核函數可以處理任意維度的特征空間,而不需要知道的具體形式。

其中,ε和C事先給定,C用來平衡模型復雜性項1/2||w||2和訓練誤差項的權重參數,表示經驗風險,由ε不敏感損失函數衡量,1/2||w||2是對函數面的量度。
引入松弛變量ξi和,以尋找系數w和b:

則問題轉化為一個凸二次優化問題,下面引入Lagrange函數:


Step4.構造決策函數

表2 各樣本銀行評價數據表
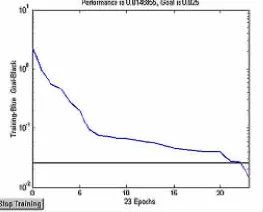
圖1 訓練樣本誤差曲線

圖2 檢驗樣本的擬合曲線
將 w 代入 y=f(x)=wφ(xi)+b,得:b,即為問題的回歸估計。
3 實例仿真
3.1 網絡算法步驟
根據上述SVM的學習算法和基于SVM的評價原理,以下具體給出多屬性評價SVM方法的實現算法如下:
Step1.根據專家意見,在任務分解后構建評價指標體系;然后準備訓練樣本數據,學習樣本輸入階段的主要任務是將學習樣本進行標準化,完成標準化工作后,將樣本集任意地分為訓練樣本和測試樣本,兩者分別用于模型訓練和精度檢驗。
Step2.訓練與學習,訓練參數輸入階段的主要任務是確定SVM模型的相應參數,如果是初次運行,則可以隨意地預定義上述參數的值,但如果是重復運行多次后,這是可采用啟發式方法進行搜尋。主要的思想是利用交叉檢驗和廣域搜索的方法,從一個較大的取值范圍內找到使交叉檢驗所得結果最好的參數。
Step3.獲得理想參數后,SVM的學習過程結束。此時的SVM便可對多屬性評價問題進行分析。
3.2 模型構建和訓練
應用基于最小二乘SVM的綜合評價方法對12家非國有獨資銀行進行仿真評價,把由專家評價得到的12組典型數據作為樣本對,數據如表2所示,數據資料來源與文獻[8]。
以表2中數據為算例,應用基于SVM的綜合評價方法進行仿真評價。在仿真實驗中,1~8組數據為訓練集,9~12組數據為測試集,模擬待評價的對象,以考察系統的泛化能力。由于RBF核函數在一般光滑性假設條件下具有良好的性能,從而非常適合于沒有更多數據額外信息的情況。因此,本算例選擇RBF函數作為SVM的核函數。基于Libsvm軟件實現SVM的求解,該軟件基于Windows操作系統,能夠實現SVM分類和回歸。SVM的參數比較多,可以利用Svmtrain的內建交叉驗證 (Cross Validation)確定SVM的參數,確定相關參數為:c=500,ε=0.005,δ2=0.01,學習結果與專家評價值十分接近,圖1為訓練樣本的誤差曲線。用測試集仿真決策的結果相對誤差最大為2.6%,最小為0.3%。圖2為檢驗樣本的擬合曲線,○為SVM輸出值,×為神經網絡輸出值,可以直觀地看出SVM的預測精度明顯優于神經網絡方法。
4 結語
本文在建立銀行經營績效評價指標體系的基礎上,提出基于SVM的綜合評價方法,并通過仿真試驗,取得了較為滿意的結果。該方法通過SVM的自學習、自適應能力和強容錯性,建立更加接近人類思維模式的定性和定量相結合的綜合評價模型。通過實例驗證,該方法避免了BP算法的缺陷,能很好地控制學習誤差,而且泛化能力強。但是,核函數的選取和SVM參數的優化問題是應用本算法的基本問題,也是本課題的進一步研究方向。
[1]N.Vapnik.The Nature of Statistical Learning Theory[M].New York:Springer-Verlag,1995.
[2]Osuna E,Freund R,Girosi F.Training Support Vector Machines:An Application to Face Detection[A].Proceeding of the IEEE Conference on Computer Vision and Pattern Recognition[C].San Juan,Puerto,Rico,1997.
[3]李文博.基于支持向量機的戰略聯盟合作伙伴選擇研究[J].科技進步與對策,2007,24(2).
[4]紀延光,徐啟華,韓之俊.基于支持向量機的R&D項目過程質量度量[J].中國管理科學,2004,12(6).
[5]杜小芳,張金隆.農產品銷量預測的支持向量機方法[J].中國管理科學,2005,13(4).
[6]袁曾任.人工神經元網絡及其應用[M].北京:清華大學出版社,1999.
[7]Xu H Y.Fuzzy Neural Networks Technique with Fastback Propagation Learning[J].Based Fuzzy Logic Contral and Pesision System,1992,1.
[8]謝赤,鐘贊.熵權法在銀行經營績效綜合評價中的應用[J].中國軟科學,2002(9).

