考慮期貨的電力市場競價風險分析
羅 霞,賴明勇 ,楊洪明
(1.湖南大學 經濟與貿易學院,長沙 410079;2.長沙理工大學 電氣與信息工程學院,長沙 410076)
隨著市場化改革和運營的深入,為規避交易風險,各國紛紛開展或即將推出電力期貨和遠期合約交易。因而,傳統單純進行現貨市場競價風險風析不符合市場實際[1-3],而考慮期貨交易的發電商競價風險分析,更能針對電力市場實際,為廣大發電企業進行風險預測與管理提供有力理論指導。
綜觀國內外關于金融市場風險理論的研究,到目前為止,電力市場金融風險的研究少之又少,且隨著電力市場化改革的深入,考慮期貨的發電商競價風險分析更是少見。另外,大部份文獻采取每日24時數據進行建模,忽略電價在每天不同時點劇烈波動性,從而不同時點電價并不具可比性的特點。
鑒于此,本文從電力市場現貨與期貨交易并存角度出發,以每天同一時點電價作為樣本數據進行建模,引入Copula模型反映現貨市場和期貨市場的相關性,并以GARCH衡量資產收益率的波動性,極值理論對收益率尾部進行建模,構建電力市場資產組合模型,通過實證分析得出北歐電力市場發電商競價動態風險(CVaR)。從而為我國電力期貨風險分析提供借鑒依據。
1 考慮期貨的電力市場競價風險分析
若記F為決策損失分布函數,β為置信水平,則VaR為的分位數:

由于VaR方法沒有考慮損失超過閾值(VaR)的情況,也存在一些數學處理上的缺點,在此基礎上,Uryasev等人給出了CVaR方法:

其中E(·)表示取期望。X表示損失超過閾值的資產。顯然,用VaR或CVaR方法來分析市場風險,最關鍵的是要刻畫出分布函數F。
本文考慮用Copula函數反映電價現貨與期貨資產相關性,GARCH模型刻畫電價資產收益率序列,一元極值理論POT方法對分布函數尾部建模,從而得到CVaR估計。
GARCH模型的期望與方差方程為:

i=1,2,代表現貨與期貨兩種資產。t為時間,rti代表收益率序列,εti為rti的波動項,Zti是i.i.d的對稱隨機變量且var(Zti)=σ2<∞。
將資產進行GARCH模型擬合后得到的殘差進行標準化處理,可以得到標準殘差:

其中,μ為條件均值,h為條件方差。
采用一元極值理論中的GPD(帕累托)分布函數對隨機擾動項(標準殘差序列)Z上下尾部,核密度估計方法對中間資產進行建模,可得到現貨與期貨電價收益率的隨機擾動項Z的邊際分布為:
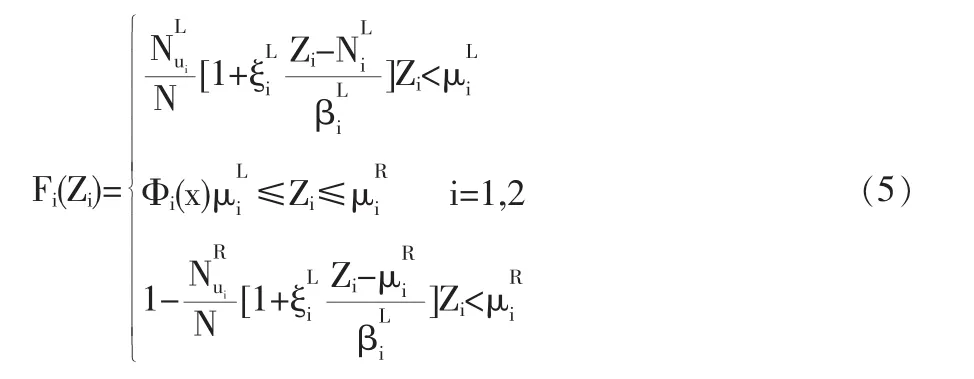
Copula函數建立了由邊際分布尋找聯合分布的方法,通過選擇合適Copula函數,得到現貨與期貨資產的聯合分布函數,并采用兩步最優化方法 (IMF方法),利用上述邊緣分布函數將隨機擾動項進行概率轉化后,估計出時變Copula參數。估計出參數值后,以此動態參數值進行Monte Catlo模擬,得到n組模擬數值u1,u2,…,un。再通過求模擬數值的逆函數 Z1,Z2,…,Zn=F-1(u1,u2,…,un),即可得到連接函數為 C,聯合分布為F的N維隨機擾動項。
在此基礎上,基于波動方程 Ri,t=μi,t+σi,tZit(i=1,…,N),運用GARCH(1,1)模擬 N 個電力資產收益率的條件均值 μi,t,條件方差 σi,t。 于是得到組合資產的收益率向量 R1,t,…,RN,t,即模擬的收益率序列。求此模擬的電價資產收益率序列CVaR值,即是考慮期貨的發電商競價動態風險值。
2 電力競價市場GARCH-EVT-Co p u la風險模型
2.1 數據分析
本文數據來源于北歐4國的電力運營機構Nordpool(詳見http://www.nordpool.com),選取2000年1月1日至2006年6月21日每天的期貨電價 (以每天周合約期貨的收盤價作為期貨電價)和現貨電價(以每天21時系統清算電價作為現貨電價)。由于周六、周日和某些特定的節假日,期貨市場不進行交易,期貨和對應的現貨電價序列不包括這些時間的數據。電價樣本數據共1611組。將電價收益率定義為,得到1610組數據。其它時點數據分析可以采取同樣方法得到相似結論。
圖1顯示出現貨和期貨電價負對數收益率曲線。可以看出收益率序列比較平穩,沒有大幅波動,但異常值出現的頻率較高,并集中出現在一個特定的時期,這種現象顯示出了波動的聚類現象。表1給出了電價期貨收益率序列(以option表示)和現貨收益率序列(以spot表示)的統計性特征,其偏度,峰度,都顯著于正態分布下的1和3,且JB正態檢驗統計量遠大于5%的臨界值,拒絕正態分布的原假設,由此反映了電價收益率序列的非正態性以及尖峰厚尾特性。
為了防止虛假回歸,對這兩個時間序列進行單位根檢驗(表2)。檢驗結果說明無論在1% ,5%還是10% 的顯著性水平下,現貨電價收益率序列和期貨電價收益率序列都是平穩的。因此可以直接用GARCH模型進行回歸,得到現貨和期貨的波動率序列。

表1 現貨與期貨收益率序列統計特征描述
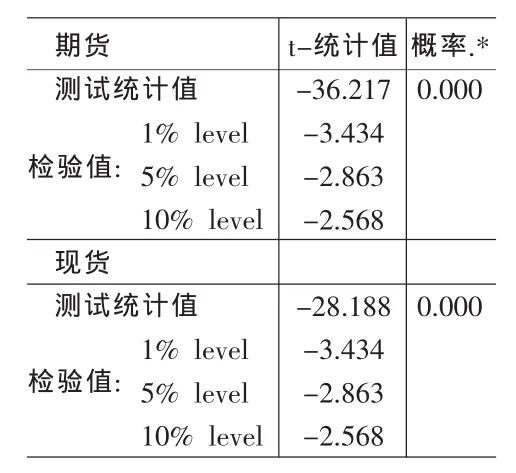
表2 現貨與期貨收益率序列單位根檢驗
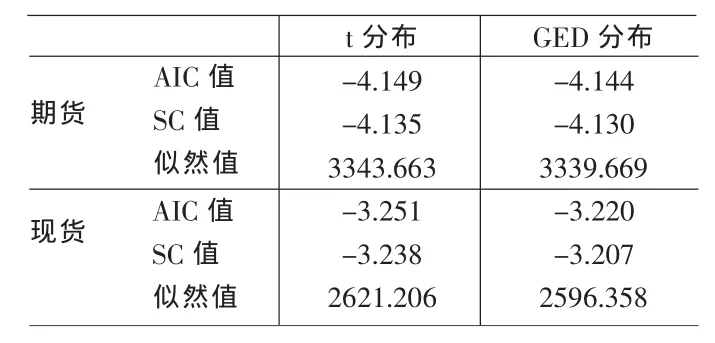
表3 現貨與期貨收益率序列的GARCH模型估計結果

表4 CDF擬合結果

表5 CVaR后驗測試--Kupiec失敗率檢驗結果

圖1 現貨與期貨負對數收益率曲線
2.2 GARCH模型選取與參數估計

圖2 擬合殘差與條件方差

圖3 期貨MEF
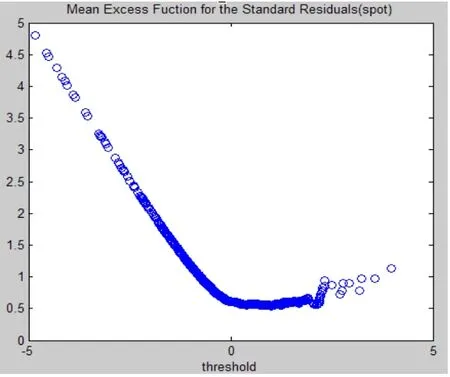
圖4 現貨MEF圖

圖5 期貨經驗CDF與GPD擬合圖
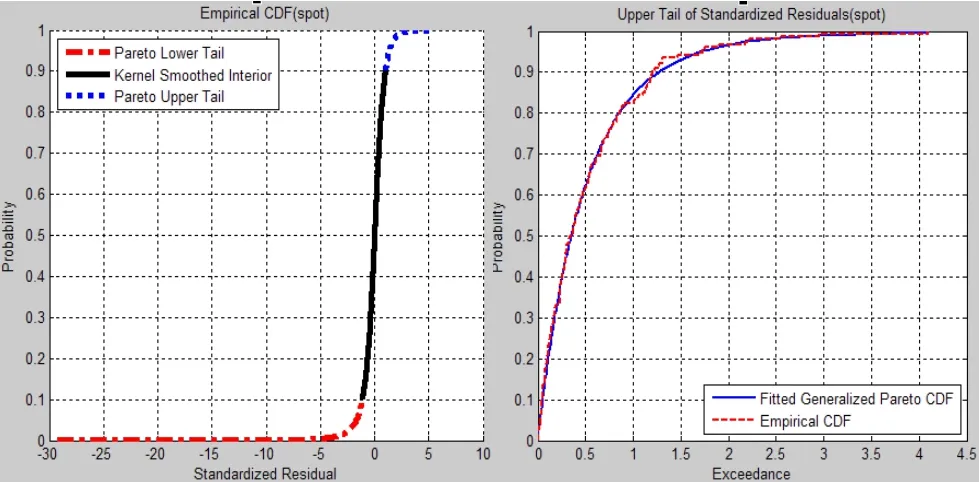
圖6 現貨經驗CDF與GPD擬合圖
為了更精確地描述電價收益率時間序列分布的尾部特征,本文運用GARCH-t和GARCH-GED模型擬合樣本數據。通過比較模型的AIC和SC值,選取最適合的邊際分布估計方法,得出結果如表3所示:
通過AIC和SC值的比較,我們得出殘差服從t分布的GARCH模型對邊際分布的擬合要優于其它分布所估計的結果。用式(3)對資產進行擬合,從而得出現貨收益率和期貨收益率的回歸方程如下:

運用GARCH擬合數據后得到擬合的殘差與條件標準方差(圖2)。將殘差用式(4)進行標準化處理,可以得到標準殘差。通過對數據進行檢驗可知,殘差獨立且是同分布的,即符合極值理論要求的(i,i,d)序列。

圖7 VaR估計與實際收益率比較圖(t-Copula)

圖8 CVaR估計與實際收益率比較圖(t-Copula)
2.3 GPD分布函數擬合
將隨機擾動項(標準殘差序列)采用POT極值理論進行建模。閾值u采用超額均值函數(MEF)選取。
從MEF圖可得相應μ值(表4)。對標準殘差序列上下尾部采用GPD分布函數擬合,中部用核密度估計方法進行擬合(圖5,6),從圖可以看出,GPD分布很好地模擬了隨機擾動項尾部的真實分布情況。
2.4 Copula函數選擇與動態CVaR估計
從圖可以看出,基于組合模型的電力市場發電商競價動態CVaR能夠測試超出VaR的風險,較好地擬合收益率序列,靈敏地反映收益率變化,從而能更加有效地度量發電商競價風險。
2.5 基于Copula的電力市場競價風險模型評估
在計算出CVaR值后,為能對模型進行評價,需要對估計結果進行返回檢驗,本文以失敗率檢驗法來衡量模型準確性。
將每一期預測的CVaR與該期實際發生的損失(現貨負對數收益率)進行比較,若預測的CVaR小于實際損失,表明預測失敗。如實際考察天數為T,失敗天數為N,則失敗頻率記為P(N/T),這樣失敗頻率就服從一個二項式分布,期望概率為P*,設零假設為 H0:P=P*,備擇假設為 H:P≠P*,檢驗失敗頻率是否拒絕零假設。Kupiec(1995)[16-17]提出了采用似然比率檢驗法對零假設檢驗,似然比方程為:

式(7)在零假設條件下,統計量LR服從自由度為1的χ分布。
測試的樣本數共有1409個,在99%和95%置信度水平下,只要滿足LR值21.666或61.55,則證明模型不能拒絕Kupiec失敗率檢驗假設的原假設,具有可預測性。
可以得出,Clayton函數與Gumbel函數嚴重高估市場風險。T連接函數能很好的預測模型,這也說明了T連接函數能反映尾部相關性,基于t-Copula函數的風險預測模型更能刻畫電力現貨資產與期貨資產相關性,從而準確度量發電商競價風險。
3 結論
本文將GARCH-EVTCopula組合模型應用于電力市場,并建立考慮期貨交易的發電商競價動態風險評估機制。具體來說,采用GARCH模型來度量電價資產收益率的波動性和異方差性,以EVT反映收益率的尾部分布,Copula函數反映電價現貨市場與期貨市場相關性,且以每天同點時刻數據建模,對北歐電力市場發電商風險進行實證分析,得出如下結論:電力資產序列存在波動聚集性,因而資產間相關性也會是時變的,故應對發電商競價風險進行動態預測與衡量。模型檢驗結果顯示,t-Copula連接函數更能體現資產相關性,能更準確度量考慮期貨的發電商動態競價風險。建議風險管理者積極推進以CVaR值為核心的風險管理模式,采取動態的總體風險控制措施,結合科學的電價模型進行更準確的風險計量與評估。
[1]N.E.Hans,H.Bysrtom.Extreme Value Theory and Extremely Large Electricity Price Changes[J].International Review of Economics and Finance,2005,(14).
[2]F.C.Kam,G.Philip.Using Extreme Value Theory Measure Value-at-risk for Daily Electricity Spot Prices[J].International Journal of Forecasting,2006,(22).
[3]Xiusong Gong,Xia Luo,Jiajie Wu.Electricity Auction Market Risk Analysis Based on EGARCH-EVT-CVaR Model[C].IEEE International Conference on Industrial Technology(ICIT2009),2009.
[4]P.F.Artzner,J.E.Delbaen,D.Heath Thinking Coherently[J].Risk,1997,(10).
[5]Rockafellar R T,Uryasev S.Optimization of Conditional Value-at-Risk[J].Journal of Risk,2000,2(3).
[6]王壬,尚金成,馮旸等.基于CVaR 風險計量指標的發電商投標組合策略及模型[J].電力系統自動化,2005,29(14).
[7]Kupiec,E H.Techniques for Verifying the Accuracy of Risk Measurement Models[J].Journal of Derivatives,1995,(2).
[8]Umberto Cherubini Elisa Lluciano, Walter Vecchiato.Copula Methords in Finance[M].England:John wiley&Sons,Ltd,2004.
[9]柏滿迎,孫祿杰.三種類型Copula-VaR計算方法與傳統VaR方法的比較[J].數量經濟技術經濟研究,2007,(2).
[10]Paul Embrechts,Andrea Hoing,Alessandro Juri.Using Copula to Bound the Value-at-Risk for Functions of Dependent Risks[J].Finance and Stochastics,2003,(7).
[11]Rank.J.Copulas in Financial Risk Management[M].London:University of Oxford,2000.

