帶強制性特別向下修正條款的可轉債定價研究
劉大巍,陳啟宏
(上海財經大學 金融學院,上海 200433)
0 引言
可轉債也稱為可轉換公司股票債券,是一種兼有股票期權和債券性質的復合型金融衍生產品。對于可轉債的發行公司而言,由于其在不同的市場條件下,會表現出債券融資和股票融資兩種不同的作用形式,上市公司可以根據其需要,更加靈活的選擇其融資方式,因此,發行可轉債已成為上市公司一種重要的融資渠道。同時,為了避免可轉債的償付方式單純的依賴于市場因素,增加公司的融資風險,發行公司還會根據其需要,對可轉債的償付方式加以控制,而其最主要的調控方式就是可轉債中設定的附加條款。
由于可轉債中的期權和債券相互嵌套,使得其定價模型較為復雜,尤其是在我國的債券市場上,絕大多數可轉債都同時含有所有的附加條款,使得對可轉債的定價非常困難。
截至2008年底,我國共有61支可轉債上市,其中的5只轉債含有強制性特別向下修正條款,這些轉債定價模型中的修正條款和回售條款所對應的條件是不能合并的,定價模型中的邊界條件和終值條件,都會有所變化。本文將詳細討論這些轉債的定價問題,并利用最小二乘蒙特卡羅方法計算其數值結果,將所得結果同市場數據進行比較分析。
1 定價模型
1.1 信用風險
由于市場上的公司債券利率往往高于同期的無風險利率水平,本文引入信用風險模型來解釋這一市場現象。可轉債債權部分的價值會受到發行公司信用風險的影響,而股權部分的價值受信用風險的影響則相對較小。因此本文中采用Tsiveriotis和Fernande(1998)[6]的信用風險模型。在此模型中,作者將可轉債價值分為相互作用的股權部分和現金部分,其中,股權部分不受信用風險的影響,因此其價值為未來的現金流以無風險利率折現的結果,而現金部分則會受到信用風險的影響,其價值為未來現金流以調整后的折現率(無風險利率加信用風險溢價)折現后的結果,如果假定可轉債標的股票價格服從幾何布朗運動dSt=μStdt+σStdWt,可轉債的價值應滿足微分方程

其中,V為可轉債價值,B為轉債中的現金部分的價值,S為標的股票的價格,σ為股票價格的波動率,r為無風險利率,rc為信用風險溢價,f(t)為債券的利息支付。
1.2 終值條件
我國帶有強制性特別向下修正條款的5只轉債中的特別向下修正條款的規定都為:當可轉債的標的股價達到或低于當前轉股價的某一比例時時,債券發行公司必須立即向下修正轉股價格,并且其修正幅度不得低于當前轉股價的一定比例,其修正次數不受限制。根據陳盛業、王義克(2007)[2]的討論,由于向下修正轉股價格相當于增加了未來可能的現金支付,也就是增大了轉債的價值,對于轉債發行公司而言,在未觸發回售條款的情況下修正轉股價格是不明智的,而且修正幅度越大,其未來要支付的現金流就越多。因此,在強制性特別向下修正條款的約束下,轉債發行公司必須向下修正轉股價,但修正幅度應為其修正義務下的最低值。
我國的可轉債在轉股期內都可以隨時轉股,持有債券直到債券期日的投資者將會根據當前的轉股價格和標的股價來決策是否轉股,而到期日的轉股價格是由標的股價的路徑決定的,因此,帶有強制性特別向下修正條款的可轉債定價模型中含有亞式期權的性質,是一種強路徑依賴期權。
由于轉股價的修正次數不受限制,只要標的股價達到修正觸發條件,轉股價格就會修正為原轉股價的特定比例,所以轉債在到期日T的轉股價格KT取決于標的股價之前所達到的最低值,只要其最低值不低于每股凈資產價值。將其表示為函數形式為:
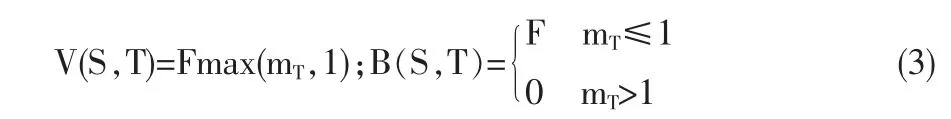
其中,F為轉債面值,mT=ST/KT。也就是說,如果在到期日的標的股價低于當時的轉股價格,則不執行轉股,債券持有者會選擇收回本息;而如果標的股價高于當時的轉股價格,則持有者會選擇以當前轉股價格進行轉股。
1.3 邊值條件
在轉股期的每一時刻t,可轉債的轉股價格Kt與之前的股價路徑有關,用函數可以表示為:轉債持有者的最優策略為當執行轉股所得支付大于或等于轉債價值時,立即轉股,也就是應有

當轉債的標的股價達到或低于回售觸發股價時,債券持有者可以將轉債以約定價格回售給發行方,此時應有
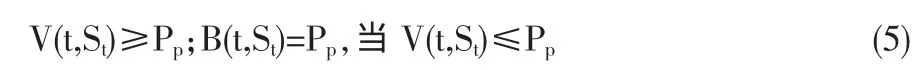
其中Pp為回售價格。
當轉債的標的股價達到或高于贖回觸發股價時,債券發行方可以將轉債以約定價格將轉債贖回,但此時債券持有者可以選擇轉股,因此有 V(t,St)≤max{StF/Kt,Pc},其中 Pc為贖回價格。而由于在我國的可轉債贖回觸發股價下一般都會滿足StF/Kt≤Pc,可將此邊界條件簡化為

1.4 數值方法
通過求解微分方程(1)-(6)就可以得到可轉債的理論價格。但由于上述帶有強制性特別向下修正條款的可轉債中嵌入了亞式期權的性質,且其依賴于標的股價路徑的支付函數較為復雜,同時還附有各種附加條款,使得其數值方法較為繁瑣。
本文采用Longstaff和Schwartz(2001)[3]提出的最小二乘蒙特卡羅模擬方法對上述模型進行求解。傳統蒙特卡羅方法的優點是對邊界條件的判斷較為方便,缺點是對于路徑依賴期權價值的計算比較困難,最小二乘蒙特卡羅方法則克服了這個缺陷。其主要步驟為:
(1)首先在當前的標的股價條件下,用離散的時間點模擬出直到到期日的若干條股價路徑;
(2)在每個時間節點處,以各條路徑上的當前股價作為解釋變量,以各條路徑上前一節點的支付貼現值作為被解釋變量,利用最小二乘方法估計在當前股價下持有轉債可以得到的未來支付的貼現值;
(3)將此估計值代入到邊界條件中,判斷當前節點處債券持有者是否應當轉股或是執行回售條款、發行方是否已向下修正轉股價格或是執行贖回條款,從而得到當前支付值,并將其貼現到前一節點;
(4)按照上述步驟,采用倒推的方法得到初始節點處的支付,最終取所有路徑的初始支付均值,即為初始時刻的轉債價格。
這種方法大大簡化了算法的復雜程度并提高了其效率。本文同時采用了對偶變數法,即使用對稱的隨機數來模擬轉債標的股價的路徑,以消除一些極端模擬路徑對計算結果的過大影響,從而提高運算精度。
2 實證分析
2.1 樣本選取及參數估計
我國目前共有5只帶有強制性特別向下修正條款的轉債,其中1只為時點修正,本文利用上述模型對另外四只轉債進行定價,其發行數據見表1。
四只轉債與邊界條件相關的附加條款見表2,其中的觸發比例和調整比例都是與當前轉股價格的比值,r為當年債券利息。
2.2 實證結果及分析
當標的股票有派發股息行為時,股票價格的波動方程應為 dSt=(μ-D)Stdt+σStdWt,其中D為連續化的股息分紅,但一般的可轉債發行時都附有相應的轉股價格調整條款,即在派發股息時,將以一定的方式向下調整轉債的轉股價格,以抵消股息分紅對轉債的影響。因此,本文有理由近似的認為可轉債標的股票派發紅利和轉股價格調整對轉股概率的影響會相互抵消,因此,仍然假定股價服從幾何布朗運動dSt=μStdt+σStdWt,同時,將可轉債的當前轉股價格作為最終的轉股價格。
本文將可轉債的定價時刻到到期日的時間間隔劃分為200個時間段,即每條模擬路徑有201個時間節點,同時模擬出標的股票價格的10000條路徑 (5000條初始路徑加5000條對偶路徑)。最終得到的四支轉債在發行一年后的理論價格與其相應的市場價格(當日開盤價)的比較見表4。
由上述表4結果可以看出采用最小二乘蒙特卡羅方法計算出的轉債價格是較為準確的,且所有數值結果均處于當天的可轉債交易的最高價格與最低價格區間內,定價結果較為理想。其中,當標的股價相對轉股價格比較接近時,市場上的轉債價格與理論價格相差很小,但當標的股價偏離轉股價格較多時,則誤差較大。筆者認為出現這種現象的原因除了參數估計產生的誤差外,主要原因在于,當轉債處于深度實值或虛值狀態時,轉債持有者會對股價運動方向產生較強的預期,偏離其理論波動路徑,使得誤差增大。

表1 可轉債樣本數據
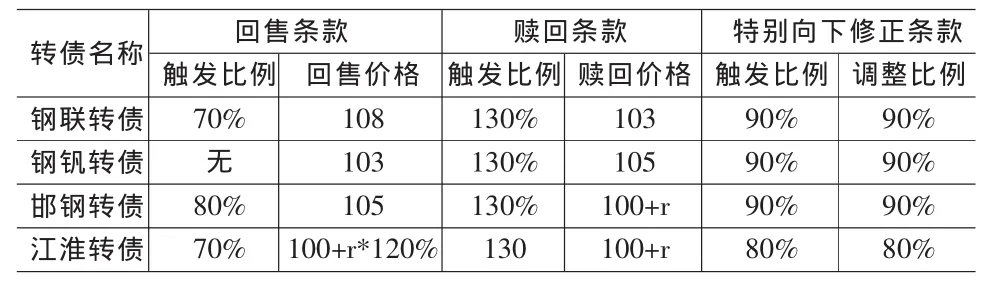
表2 可轉債樣本附加條款數據

表3 可轉債樣本年利率數據
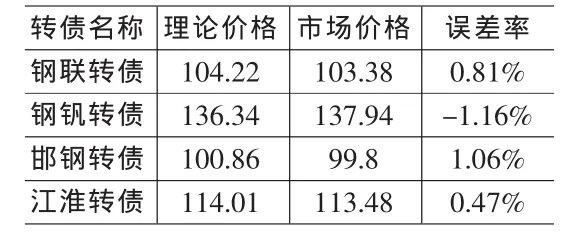
表4 可轉債樣本理論價格與市場價格比較
3 結束語
我國市場上帶有強制性特別向下修正條款的可轉債中嵌套的期權具有亞式期權的性質,其定價模型中的終值條件和邊界條件與普通的可轉債定價模型有很大差別,模型的求解也更為困難。本文按照亞式期權的模型對其定價方法進行了詳細的分析,并利用最小二乘蒙特卡羅模擬方法對此模型進行了求解,從最終的數值結果可以看出,定價結果十分理想,我國此類轉債的市場價格與理論價格非常吻合。
[1]陳盛業,王義克.奇異期權與中國可轉債定價[J].清華大學學報(自然科學版),2007,47(6).
[2]Tsiveriotis K,Fernandes C.Valuing Convertible Bonds with Credit Risk[J].Journal of Fixed Income,1998,8(2).
[3]Longstaff F,Schwartz E.Valuing American Options by Simulation:A Simple Least-squares Approach[J].The Review of Financial Studies,2001,14(1).

