復合LINEX對稱損失下Poisson分布參數的Bayes估計與應用
韋程東,韋 師,蘇 韓
(廣西師范學院 數學科學學院,南寧 530023)
0 引言
Poisson分布是概率論中一種重要離散分布,在實際生活中有著廣泛的應用,例如,某地區在一天內郵遞遺失的信件數、某醫院在一天內急診病人數、某一地區一個時間間隔內發生交通事故的次數、在一個時間間隔內某種放射物質發出的、經過計算器的α粒子數等都服從Poisson分布。對Poisson分布的研究不僅在某些方面可以提高工作效率,還可以提高經濟效益,因此對Poisson分布的研究具有重要的理論價值和實際意義。
國內外對Poisson分布已有一定的研究,王德輝等[1]研究了熵損失下Poisson分布參數倒數的估計,俆寶等在文獻[2]中研究了Poisson分布參數倒數在一種對稱損失下的Bayes估計,荊雷[3]在其碩士學位論文中,在Q-對稱熵損失函數下研究了Poisson分布的參數估計,韋瑩瑩等[4]討論了Q-對稱熵損失下Poisson分布參數倒數的估計問題。而張睿[5]已研究了復合LINEX對稱損失函數下正態分布及指數分布的參數估計并證明其可容許性。本文主要在復合LINEX對稱損失函數下,研究Poisson分布參數λ的Bayes估計。并舉出具體的例子說明其應用性,最后通過數值分析來驗證該Bayes估計的合理性。
設隨機變量X服從參數λ的Poisson分布,則其分布律為

當隨機變量 X 服從(1)式的 Poisson分布時,設(X1,X2,…,Xn)為來自總體X 的容量n的隨機i:i:d樣本,(x1,x2,…,xn)為其觀測值,則其聯合密度函數為
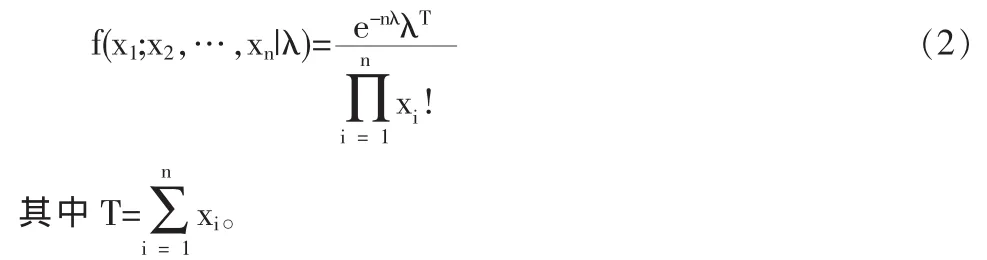
在文獻[5]中張睿提出的復合LINEX對稱損失函數,其表達形式如下

很顯然該損失函數的函數不僅是非負的,且該損失函數是 嚴 格 凸 函 數 。 事 實 上 由 于 L (θ,δ)=e-a(θ-δ)+ea(θ-δ)-2≥22=0,所以損失函數的函數是非負的。又在式(3)中對 δ 求偏導得 L'(θ,δ)=ae-a(θ-δ)-aea(θ-δ)。 任取 0<δ1<δ2,那么就有:
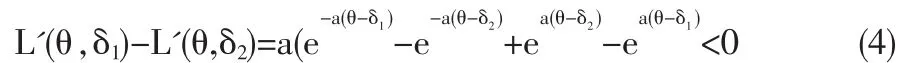
即 L'(θ,δ1)-L'(θ,δ2)<0,所以對稱損失函數 L(θ,δ)關于 δ 是嚴格凸函數。
1 參數λ的Bayes估計
在這一節,我們討論參數λ的Bayes估計。記X=(X1;X2;…,Xn),對任意先驗分布,λ 的Bayes估計為 δ(X)n(E(eaλ|X)/E(e-aλ|X)),這可由下面的定理得到。
定理1 在復合LINEX對稱損失函數(3)下,對任何先驗分布 π(λ),λ 的 Bayes估計為:

證明 設δ(x)為λ的任一估計,在損失函數(3)下,由定義得 δ(x)的 Bayes風險為

上式左端 E[L(λ,δ)]表示的是關于 λ 與樣本 X1,X2,…,Xn的聯合分布取期望,所以要求λ的Bayes解,只要求極小化E{[e-a(λ-δ)+ea(λ-δ)-2]|X}即可。 令
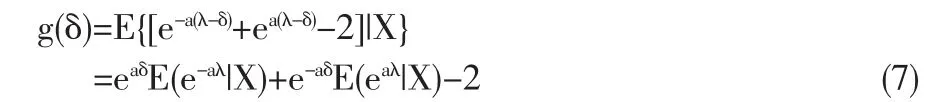
再對其關于δ求導并令其等于0即:


所以函數g(δ)是關于δ的嚴格凸函數。從而知δ(x)是函數g(δ)唯一的極小值點,所以 λ 的 Bayes解為 δ(x)n(E(eaλ|X)/E(e-aλ|X))。
選取 Γ(α,β)為 Poisson分布參數 λ的先驗分布,則先驗分布的密度函數為

由Bayes公式得參數λ的后驗密度為

則Poisson分布參數λ的Bayes估計,可由如下定理得出。
定理2 在復合LINEX對稱損失函數(3)下,對于先驗分布為 Γ(α,λ),Poisson 分布參數 λ 的 Bayes估計為:

下面證明該Bayes估計的兼容性,先引進一個引理:
引理1[6]給定一個統計決策問題,δ(x)是一個決策函數。若δ(x)是某個先驗分布π(λ)下的唯一的Bayes決策函數,則δ(x)必是次統計決策問題的容許決策函數。
由于復合LINEX對稱損失函數是嚴格的凸函數,所以在此損失函數下的Bayes估計也是唯一的,則由引理1可得該Bayes估計是可容許的。
2 舉例
例1 已知某細胞單位所含白血球的個數服從Poisson分布,對1008個細胞單位進行觀察,數據見表1。

表1 白血球分布情況
其中k表示細胞單位含白血球的個數,nk表示1008個觀測單位中,含k個白血球的細胞單位個數。
根據這些數據用第1節所給出的參數λ的Bayes估計,估計出白血球所服從的Poisson分布的參數λ。取a=2,計算結果見表2。
例2某實驗室在2608個相等時間單位內觀察了一種放射性物質所釋放出來的α-粒子的個數,結果如下表所示:其中頻數nk表示在2608個時間單位中釋放出k個粒子的時間單位的個數。

表2 參數λ的Bayes估計

表3 白血球分布情況

表4 參數λ的Bayes估計
根據這些數據用第1節所給出的參數λ的Bayes估計,估計出這種放射性物質所釋放出來的α-粒子所服從的Poisson分布的參數λ。取a=2,計算結果見表4。
從例1(單位細胞中白血球的分布)和例2(放射性物質釋放的α-粒子的分布)我們可以看到Poisson分布參數的Bayes估計在實際生活中的應用,此外Poisson分布參數的Bayes估計還可以應用到郵遞遺失的信件數、醫院急診病人數、交通事故的次數等實際生活中。
通過例1中的Table2中參數λ的Bayes估計的估計值可以顯示,參數λ的Bayes估計很穩定,橫向極差最大只有0.005,而縱向極差最大也僅有0.009。所以從統計決策穩健性的角度去考慮,該估計值很穩健。
通過例2中的Table4中參數λ的Bayes估計的估計值可以顯示,參數λ的Bayes估計也很穩定,橫向極差最大只有0.001,而縱向極差最大也僅有0.004。所以從統計決策穩健性的角度去考慮,該估計值復合統計決策中估計的穩健性。
根據以上的數值分析我們可以驗證本文所研究的Poisson分布的Bayes估計是合理的。
[1]王德輝,賴民,宋立新.熵損失下Poisson分布參數倒數的估計[J].吉林大學自然科學學報,2000,(4).
[2]徐寶,于春艷,孫憲軍.一種對稱損失下Poisson分布參數倒數的Bayes估計[J].吉林師范大學學報:自然科學版,2006,(3).
[3]邢蕾.Q―對稱熵損失函數下的Poisson分布的參數的估計[D].長春:吉林大學碩士學位論文,2006.
[4]韋瑩瑩,韋程東,薛婷婷.Q-對稱熵損失下Poisson分布參數倒數的估計[J].廣西師范學院學報:自然科學版,2007,24(2).
[5]張睿.復合LINEX損失下的參數估計[D],大連:大連理工大學碩士學位論文,2007.
[6]范金城,吳可法.統計推斷導引[M].北京:科學出版社,2001.

