高速薄壁圓柱滾子軸承擬靜力學分析
蘇 敏,付金輝,鄭紅威,鄧四二
(1.洛陽LYC軸承有限公司,河南 洛陽 471039;2.河南科技大學 機電工程學院,河南 洛陽 471003)
高速薄壁圓柱滾子軸承套圈的結構變形直接影響其動力學性能和使用壽命,因此在圓柱滾子軸承設計時需要考慮套圈結構變形的影響。柔性支承的滾動軸承性能分析早就引起很多學者的關注,文獻[1]在游星齒輪軸承動力學分析中,考慮了因游星齒輪支承引起的軸承套圈結構變形因素,提出了一種柔性支承的軸承力學分析方法;文獻[2-3]利用有限元法對帶有軸承外圈結構變形的滾動軸承性能進行了分析;文獻[4]在給出簡化的套圈變形表達式基礎上,對柔性套圈的圓柱滾子軸承進行了性能分析。這里針對高速薄壁圓柱滾子軸承,在考慮轉速對軸承套圈影響的基礎上,給出薄壁套圈的結構變形解析式,利用擬靜力學分析方法對軸承的動態性能進行分析。
1 數學模型
高速薄壁圓柱滾子軸承在徑向載荷作用下,套圈將發生變形。套圈的變形不僅含有滾子與其之間的局部彈性接觸變形,還有自身離心力引起的脹大變形和徑向載荷引起的變形。在此對這些變形分別處理,并假設各個變形互不影響。
1.1 結構變形
滾子與套圈之間的局部彈性接觸變形量(位置角為ψj的第j個滾子分別與內、外圈的接觸變形)由滾子和內圈間接觸變形量δij及滾子和外圈間接觸變形量δej決定。
軸承在高速旋轉時會產生很大的離心力,它所引起的脹大變形對保持架和套圈都有影響,分析時可以將套圈視為薄壁圓環。薄壁圓環在高速旋轉時,由轉速引起的內、外半徑的增量為[5]:
(1)
(2)
式中:δc,i為圓環內徑面增量;δc,e為圓環外徑面增量;ρ為圓環密度;Ω為圓環旋轉角速度;E為圓環彈性模量;ν為圓環泊松比;ri為圓環內半徑;re為圓環外半徑。
軸承內、外圈因離心力而產生的徑向變形會改變徑向游隙,將(1)式和(2)式分別應用于外圈內徑面和內圈外徑面可得到軸承徑向游隙變化值。安裝過盈量和內、外圈工作溫度差也將影響徑向游隙,為了更好地控制工況參數對離心力膨脹的影響,在軸承性能分析時,軸承徑向游隙初始值輸入應是考慮過盈配合和熱效應影響后的值。
圖1為單個線接觸載荷引起的套圈橢圓變形,用Fourier級數表示為:
(3)
式中:Kk(k=0,1,2,…)為剛度系數;W為徑向載荷;θ為變形位置與載荷的夾角。
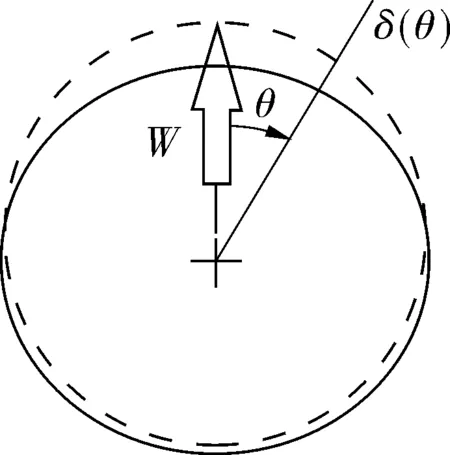
圖1 空心圓柱體在單一載荷下的變形
如果套圈受N個線載荷,可得其徑向變形量δ(θ)為:
(4)
式中:單個接觸載荷Wj與滾子的位置角ψj=(2π/N)(j-1)相對應(圖2)。文中定義位于軸承徑向載荷作用線上的滾子的位置角為0度,滾子編號為1,其他滾子沿逆時針方向依次類推。薄壁套圈結構變形時可將其作為薄壁圓環進行分析,根據文獻[6]的假設,薄壁圓環在受到純徑向載荷作用時,切應力沿壁厚方向可視為均勻分布。文獻[4]結合軸承內部受力情況,在(3)式和(4)式的基礎上給出了簡化的套圈變形求解公式,只需要3個剛度系數即可求出薄壁套圈的結構變形。
δ(θ)=W(K0+K1cosθ+K2cos 2θ)
(5)
式中:K0,K1,K2可按文獻[4]中的方法進行計算。由(1)~(5)式可求得第j個滾子處內、外圈的結構變形量為:
Defij=0.5δc,e+δi(ψj)
(6)
Defej=0.5δc,i+δe(ψj)
(7)
式中:Defij為內圈在第j個滾子處的結構變形;Defej為外圈在第j個滾子處的結構變形。
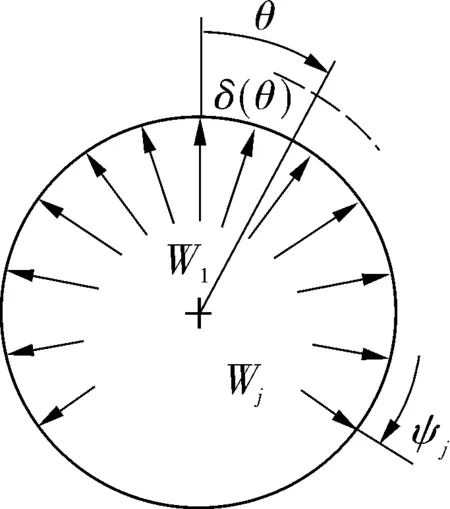
圖2 軸承在徑向載荷作用下滾子與套圈載荷分布
1.2 滾子和套圈平衡方程組的建立
考慮軸承平穩運轉,并忽略滾子歪斜。內圈以角速度ωi旋轉,外圈以角速度ωe相對于內圈反向旋轉。滾子徑向受力如圖3所示,Qij,Qej分別為第j個滾子與內、外圈接觸載荷;F為滾子離心力;Fc1j和Fc2j為第j個滾子與保持架的摩擦力,在受載區,滾子推動保持架運動,僅存在Fc1j,在非受載區,保持架推動滾子運動,僅存在Fc2j。
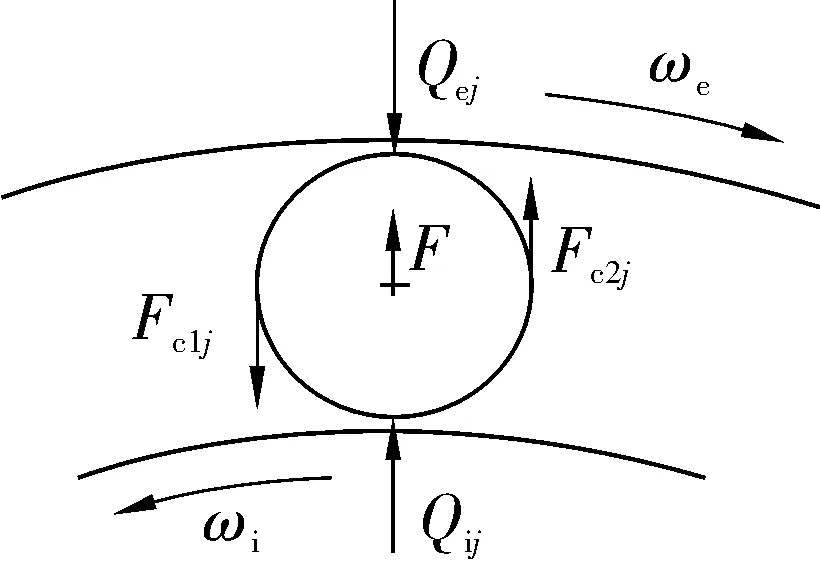
圖3 滾子徑向受力
滾子力平衡方程為:
Qij-Qej+F+Fc2j-Fc1j=0
(8)
軸承在徑向力Fr作用下,內圈的平衡方程為:
(9)
內、外圈間的相對位移需要引入幾何關系來說明,見圖4。其包括滾子與內、外滾道接觸區的彈流潤滑油膜厚度(hij,hej)、滾子與套圈接觸變形(δij,δej)、徑向游隙(Gr)、結構變形(Defij,Defej)和內圈相對于外圈的徑向位移(δr)。它們之間的關系可以表示為:
(Gr/2+δij+δej-hij-hej+Defij+Defej)-
δrcosψj=0
(10)
由(8)~(10)式組成的方程組中共有2N+1(N為滾子個數)個方程,由于Fc1j和Fc2j相對于Qij和Qej極小,可忽略不計,因此共有2N+1個未知數,即每個滾子與內、外圈的接觸法向載荷(Qij,Qej)和內圈相對外圈的徑向位移(δr)。采用BFGS數值計算法求解,可得出圓柱滾子軸承的動態特性參數。
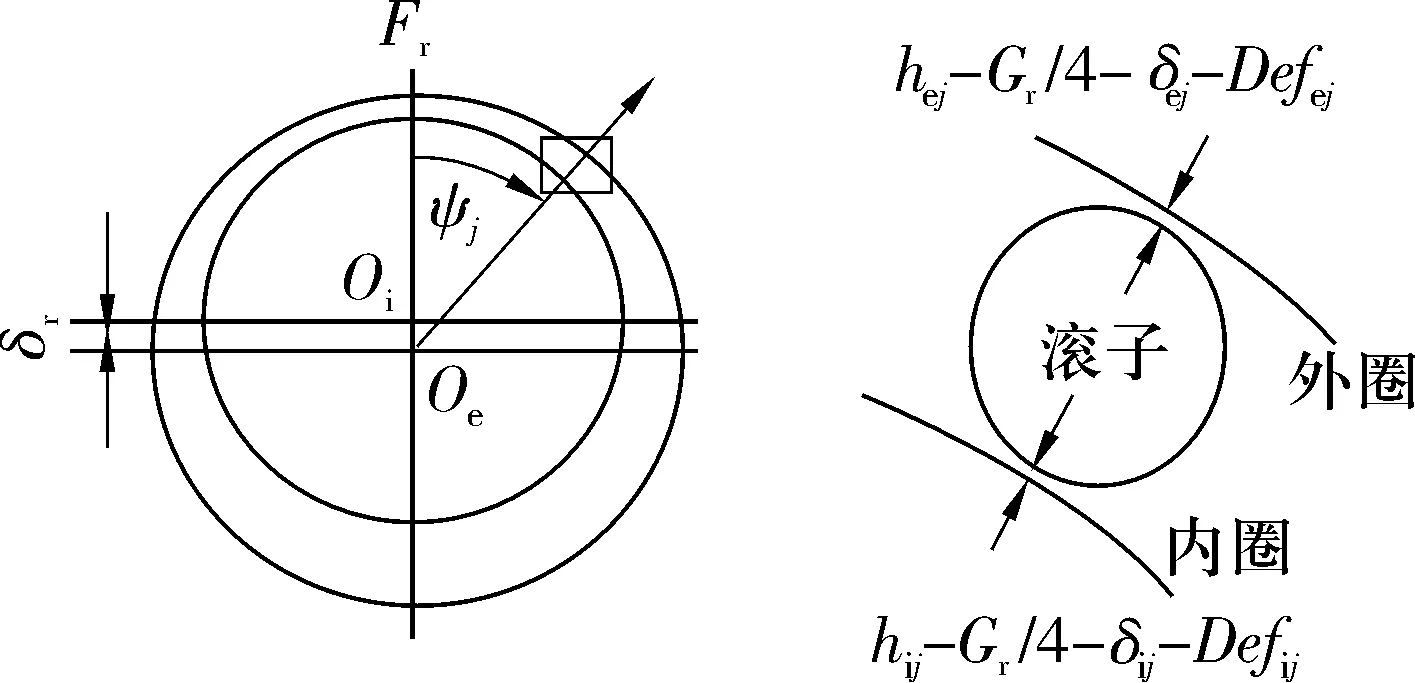
圖4 幾何關系
2 計算分析
以某型號高速圓柱滾子軸承為例進行分析,其相關參數見表1。該軸承在實際工作中內、外圈反向旋轉,內圈轉速為12 000 r/min,外圈轉速為8 000 r/min。圖5為軸承在Fr=4 kN時,套圈分別按剛性和柔性計算時的載荷分布。由圖5可知:當套圈為剛性時,有11個滾子受載;當套圈為柔性時,受載滾子個數增加到13個。柔性套圈滾子受載區域增大,并且柔性套圈的滾子與滾道間最大接觸載荷比剛性套圈的滾子與滾道間最大接觸載荷要小。
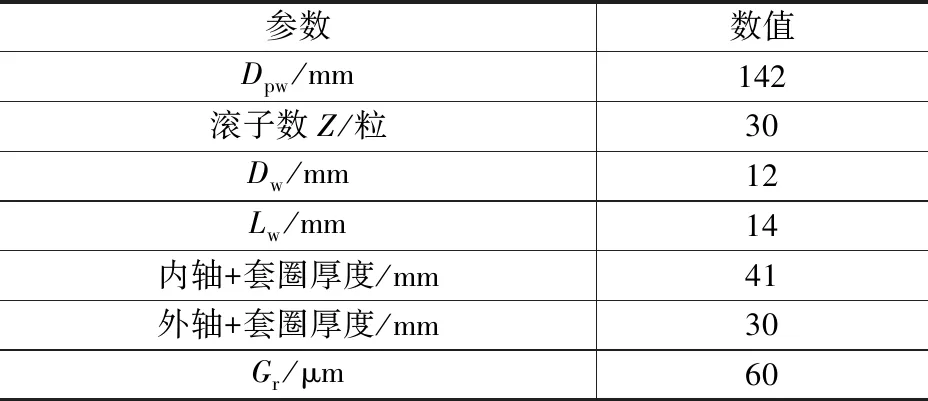
表1 圓柱滾子軸承參數
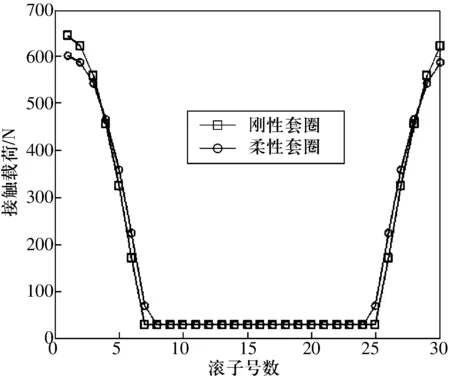
圖5 滾子與內圈接觸載荷分布
根據文獻[7]的計算方法,圖6給出了軸承在不同徑向載荷下,套圈分別為柔性和剛性時軸承疲勞壽命理論計算值。由圖6可知:軸承疲勞壽命隨著軸承徑向載荷的增大而降低,柔性套圈軸承的壽命略高于剛性套圈軸承的壽命,在載荷較大時尤為明顯。這是因為載荷較大時,柔性套圈的結構變形較大,使最大接觸載荷減小越明顯,從而減小了最大接觸載荷,提高了軸承的疲勞壽命。
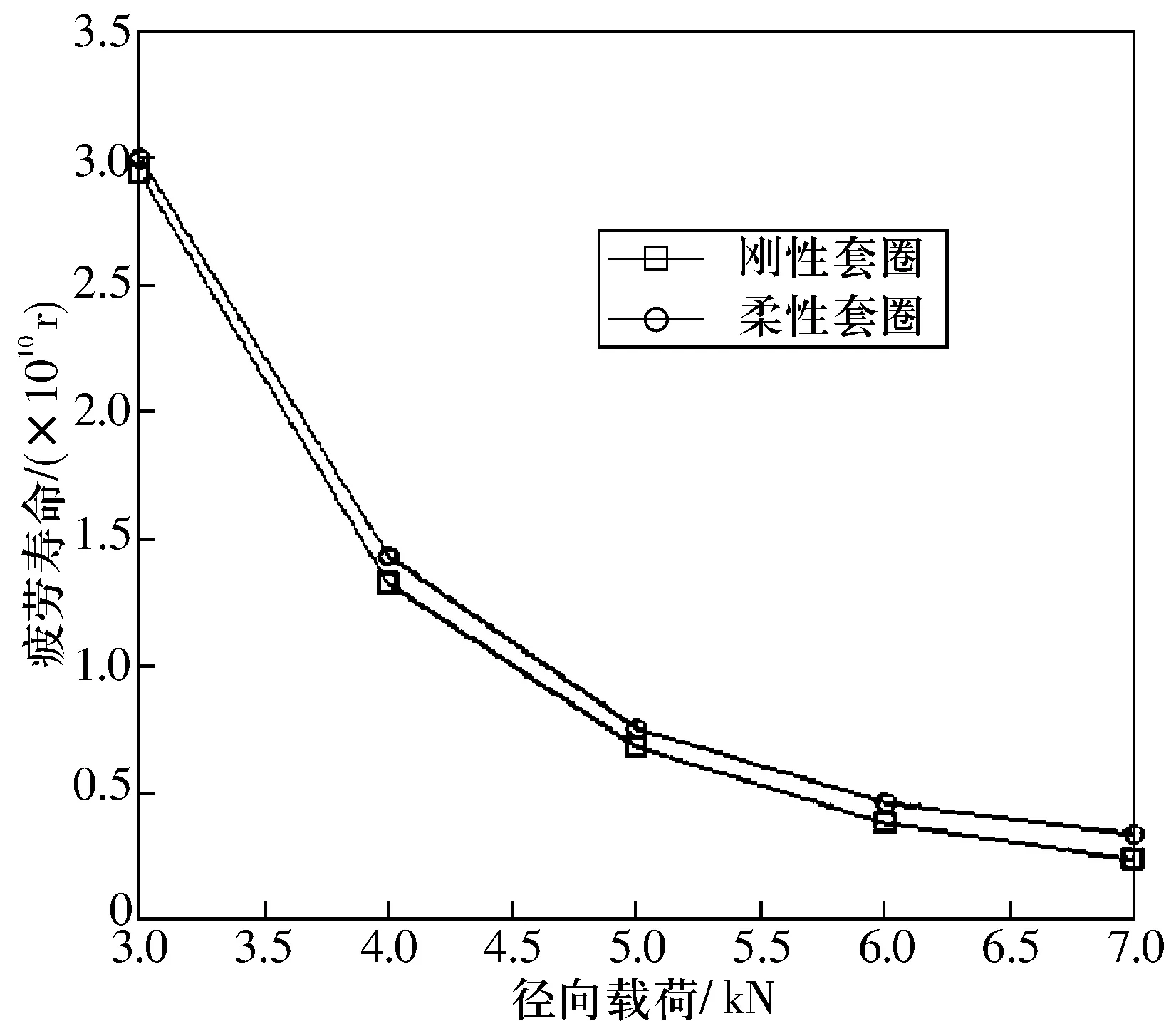
圖6 徑向載荷與疲勞壽命的關系
圖7為軸承在Fr=3 kN情況下,內圈厚度不變,外圈壁厚與外徑之比為0.082~ 0.123的滾子與外滾道間接觸載荷變化曲線。由圖7可知:當工況相同時,隨著套圈厚度變大,套圈結構變形逐漸減小。當套圈厚度與其外徑之比大于0.123時,套圈變形很小,對載荷分布的影響不大。
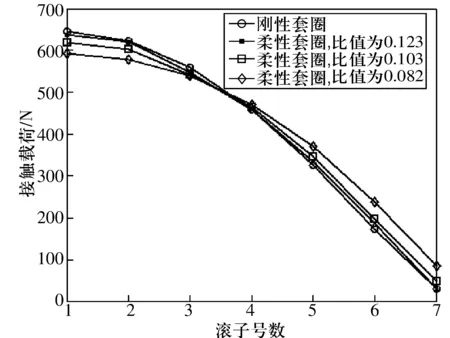
圖7 套圈厚度與接觸載荷的關系(Fr=3 kN)
圖8為內、外圈壁厚不變情況下,Fr=1,2,3 kN時滾子與外滾道間的接觸載荷變化曲線。由圖8可知:隨著Fr的增大,套圈的結構變形越來越明顯。當Fr很小時,套圈基本上沒有變形。
3 結論
(1)柔性套圈下滾子受載區域比剛性套圈下滾子受載區域大;柔性套圈下滾子與滾道間最大接觸載荷比剛性套圈下滾子與滾道間最大接觸載荷小;在一定的工況下,柔性套圈有利于軸承疲勞壽命的提高。
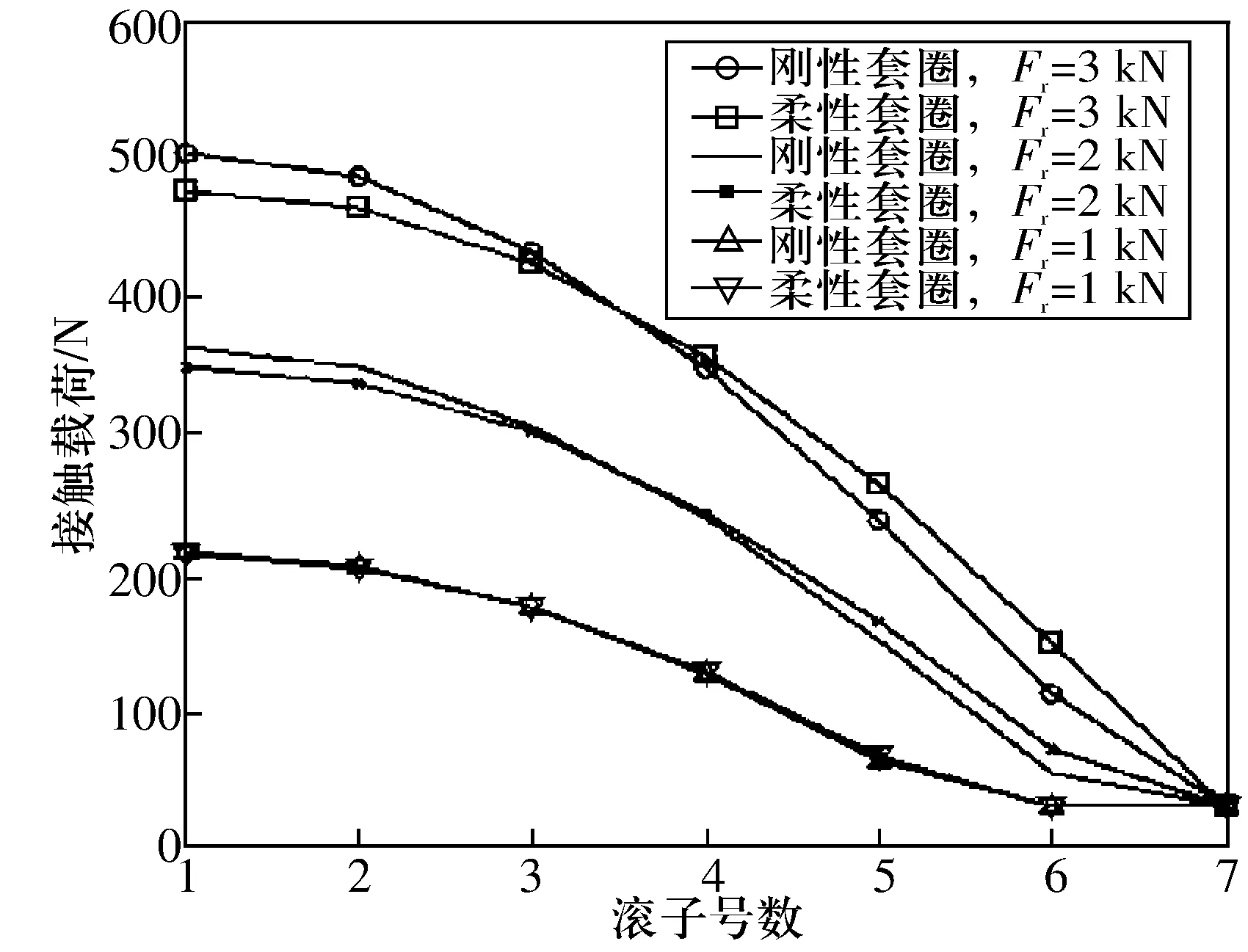
圖8 徑向載荷對滾子載荷分布的影響
(2)在套圈材料不變的情況下,套圈厚度與徑向載荷是影響套圈變形的主要因素。當套圈很薄或徑向載荷很大時,套圈結構變形明顯;當套圈很厚或徑向載荷很小時,套圈結構變形較小。在工程應用中,當軸承承受較大徑向載荷,套圈厚度與其外徑之比又很小時,必須考慮套圈的柔性。

