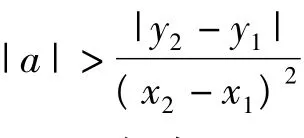平面上的兩點與二次函數圖像之間有意義的探究

●凌云志 (黃山區教育局教研室 安徽黃山 245700)

我們知道“經過平面上2個點的圓有無數個且圓心都集中在這2個點的中垂線上”，這也啟發我們去探究：經過平面上任意2個點的拋物線是否也有無數個?即便能夠明確經過2個點的拋物線有無數個，那能否按照某種需求來選擇或明確經過已知2個點的拋物線呢?順延這條思路，深挖下去，會顯出豐實的寶藏.

探究1 經過平面上任意2個點的拋物線是否有無數條?

在平面直角坐標系Oxy中，若有一條曲線y=ax2+bx+c經過任意給定的2個點 A(x1，y1)，B(x2，y2)，則由c為參量，得c可以取到無數個不同的值使得a≠0，可知過點A，B的拋物線有無數條;

(2)當x1x2(x1-x2)=0時，不能由方程(1)來明確a的解，這時雖然找到與y軸平行的對稱軸且過點A，B的拋物線很難，但可以適當地重新選擇坐標系O'x'y'(將原坐標系平移后再旋轉)，使得點A，B 在新坐標系下的坐標為 A(x1'，y1')，B(x2'，y2')，并滿足 x1'x2'(x1'-x2')≠0.仿照(1)的推導，如圖1所示，過點A，B的拋物線也有無數條.因為式(2)可以看做a是c的一次函數，a與c是互定關系，所以取定a后，b，c也就隨之確定，于是得結論1.

結論1 經過平面上任意2個點 A(x1，y1)，B(x2，y2)的拋物線總有無數條.只要滿足條件：x1x2(x1-x2)≠0，則可以選擇任意開口大小和開口方向不同的拋物線經過這2個點，但對明確了的開口大小和開口方向的拋物線有且只有1條.

探究2 對于滿足條件：x1x2(x1-x2)≠0的點A(x1，y1)，B(x2，y2)，如何選擇適度的開口大小的拋物線，使得拋物線經過這2個點時，不被其對稱軸分開.

圖1

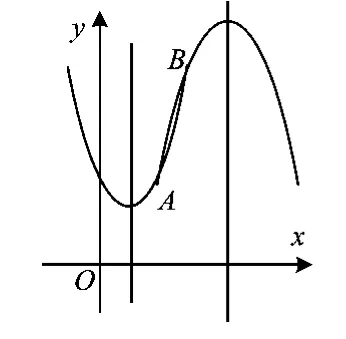
圖2

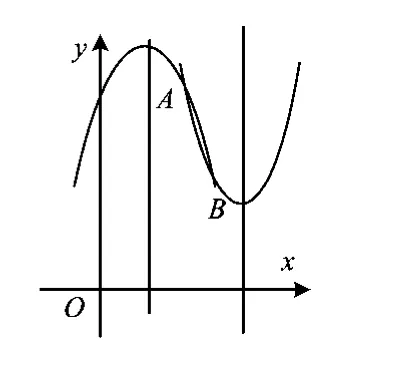
圖3

若約定：點A在點B的左邊(x1＜x2)，則點A與點B的相對位置有3種情況：(1)如圖2，點A在點B的下方(y1＜y2);(2)如圖3，點A在點B的上方(y1＞y2);(3)點A與點B一樣“齊”(y1=y2).

先就圖2所示的第1種情況展開討論：為使過點A，B的拋物線的對稱軸不將2個點分開，因拋物線開口向上，點A，B只能位于對稱軸的右側(允許點A可以在對稱軸上)，這時

若選擇的拋物線開口向下(圖3所示的第2種情況)，點A，B只能位居對稱軸的左側(允許點B在對稱軸上)，因對稱軸方程為

綜合式(3)和式(4)，不論拋物線開口向上還是向下，對圖2中的情形，為使過點A，B的拋物線的對稱軸不將兩點分開，拋物線開口大小必須滿足：

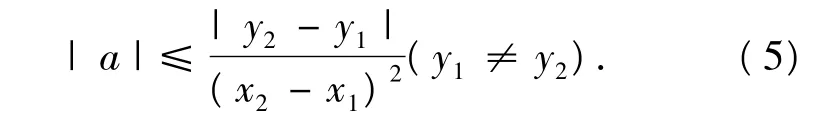
最后，當y1=y2時，顯然任何經過點A(x1，y1)，B(x2，y2)的拋物線，點 A，B 一定是拋物線對稱軸的對稱點，不可能找到滿足條件的拋物線.反映在式(5)上的要求：|a|≤0，解得a=0(拋物線不存在)，同樣得到說明.

探究3 反過來，是否經過點A(x1，y1)，B(x2，y2)的拋物線y=ax2+bx+c，滿足條件(5)就一定不被拋物線的對稱軸分開呢?

就圖4所示的情況進行分析：假定在開口向上的拋物線的對稱軸的2邊任意取點A(x1，y1)，B因此可以將條件統一為(x2，y2)，設頂點 M(m，l)，于是

由 y2=a(x2-m)2+l，得

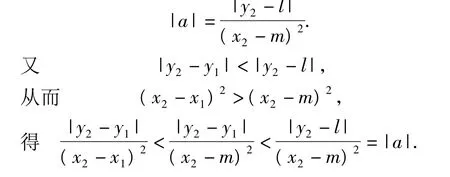
圖4

圖5

說明 落在拋物線上的對稱軸的2邊任意2個點是不會滿足條件(5)的.有興趣的讀者可以去研究圖5所示的情況，結果一樣.