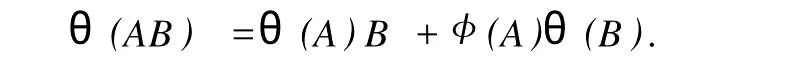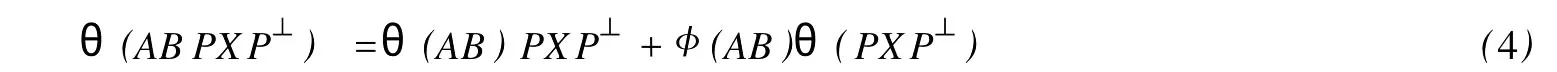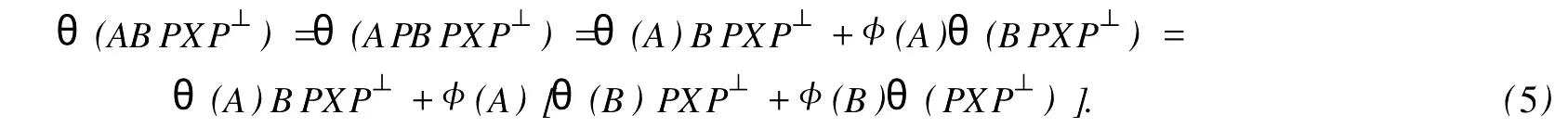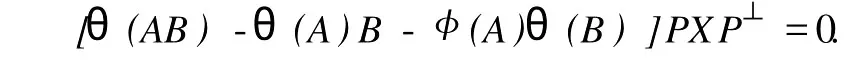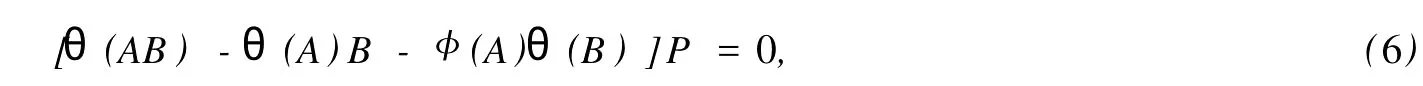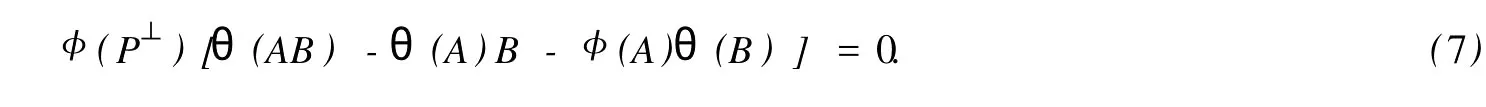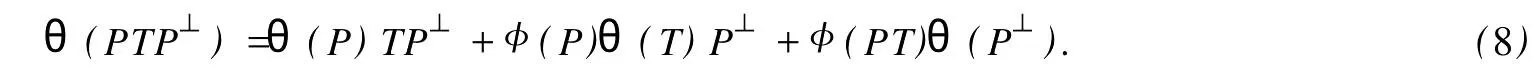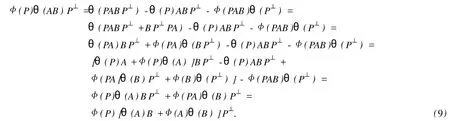套代數上的2-局部φ-導子*
吳瑞華,呂 川
(中國石油大學數學與計算科學學院,山東東營257061)
套代數上的2-局部φ-導子*
吳瑞華,呂 川
(中國石油大學數學與計算科學學院,山東東營257061)
從代數的結構和映射的特征出發,研究了套代數上的2-局部φ-導子,證明了套代數上的2-局部φ-導子都是φ-導子.
2-局部φ-導子;φ-導子;套代數
引言
首先給出幾個定義,設A是一個代數,φ是A上的一個自同構,η是A上的一個線性映射.如果對任意的a∈A有η(a2)=η(a)a+φ(a)η(a),則稱η是一個Jordanφ-導子;如果對任意的a,b∈A有η(ab)= η(a)b+φ(a)η(b),則稱η是一個φ-導子;如果對任意的a∈A,都存在A上的一個φ-導子ηa(依賴于a)使得η(a)=ηa(a),則稱η是一個局部φ-導子;如果對任意的a,b∈A都存在A上的一個φ-導子ηa,b(依賴于a,b)使得η(a)=ηa,b(a);η(b)ηa,b則稱η是一個2-局部φ-導子.Kadision[1]首次研究了算子代數的局部映射問題,局部導子和2-局部導子的概念是由Kadision[1]、Larson Sourour[2]和Semrl[3]引入的,在此研究一類更一般的映射2-局部φ-導子.由于局部映射不僅對算子代數的上同調群起著十分重要的作用,而且為人們設計滿足不同需要和具有特殊性質的映射從而解決相關問題提供了一種可能,因此它已成為算子理論和算子代數的重要研究課題之一,吸引了一大批數學家投身其中,并出現了豐富的相關研究成果[1,2,4~6].在過去的幾十年里,φ-導子已在純代數中進行了廣泛的研究[7~11]并應用于相關領域[12].本文研究一類更一般的映射2-局部φ-導子.導子成立的某些結論2-局部φ-導子是否也成立?在此主要研究套代數上的2-局部φ-導子何時成為φ-導子.
設H是可分Hilbert空間,B(H)表示H上的全體有界線性算子,B(H)上的套N是指B(H)中的一個全序投影族,它包含0和I且在強算子拓撲下是閉的.對N中的每一個投影P,記P+=inf(Q∈N◇Q>P}和P-=sup{Q∈N◇Q 以下總假設φ是τ(N)上的自同構,θ是τ(N)上的2-局部-φ-導子. 引理1 (a)如果A,B∈τ(N)使得AB=0,那么θ(A)B+φ(A)θ(B)=0. (b)對任意的A,X,B∈τ(N)有: 證明 (a)對任意的A,B∈τ(N)且AB=0,由δ的定義知,存在一個依賴于A,B的φ-導子θA,B滿足θ(A)=θA,B(A),θ(B)=θA,B(B).因此就有 (b)設A∈τ(N),由θ的性質,存在一個依賴于A,A2的φ-導子θA,A2滿足θ(A)=θA,A2(A),θ(B)=θA,A2(B).所以有 在上式中用A+X替代A可得 再在上式中用AX+XA替代X則得 將上式中的A替換為A+B,則對任意的A,X,B∈τ(N)即可證得 證畢. 引理2 如果P是N中的投影,那么對任意的X∈B(H)有 證明 對任意的P∈N,X∈B(H),由引理1得 另一方面 這說明有φ(P)θ(PXP⊥)=φ(P)θ(PXP⊥)P⊥+φ(PXP⊥)θ(P⊥). 因此得θ(PXP⊥)=φ(P)θ(PXP⊥)P⊥+θ(P)PXP⊥+φ(PXP⊥)θ(P⊥).證畢. 引理3 對任意的A∈τ(N)和P∈N都有 證明 由引理1(b)得 所以φ(P)θ(PAP⊥)P⊥=θ(P)θ(P)AP⊥+φ(P)θ(A)P⊥+φ(PA)θ(P⊥)P⊥,由引理2有 由式(1),(2),(3)得θ(PA)=θ(PAP)+θ(PAP⊥)=θ(P)A+φ(P)θ(A)和 θ(AP⊥)=θ(PAP⊥)+θ(P⊥AP⊥)=θ(A)P⊥+φ(A)θ(P⊥).證畢. 在引理3中令A=I可得以下推論: 引理4 如果P是N中的投影,那么對任意的A∈τ(N),X∈B(H),有 證明 設P∈N任意的A∈τ(N),X∈B(H),T∈B(H),引理1~3說明 同理可證(b)式也成立.證畢. 下面的定理1是本文的主要結果 定理1 設N是B(H)中的任意一個套,φ是τ(N)上的自同構,θ是τ(N)上的一個2-局部φ-導子(沒有連續性的假設).則對任意的Α,Β∈τ(N)有 此定理說明了套代數上的任意2-局部φ-導子都是φ-導子. 證明 設A,B∈τ(N),P為N中的一個固定非平凡投影.對任意的X∈B(H)由引理4(a)得 另一方面,再由引理4(a)得 據式(4),(5)對任意的X∈B(H)有 因此, 同理由引理4(b),得 由引理3,任意T∈τ(N)有 從而由式(8)和引理1,3有 由式(6),(7),(9),對任意的A,B∈τ(N),就有θ(AB)=θ(A)B+φ(A)θ(B).也就是說明θ是一個φ-導子.證畢. 參考文獻: [1]Kadision R V.Local derivation[J].Algebra,1990,130:494-509. [2]Larson D R,SourourA R.Local derivations and local automorphis ms of[J].Proceedings Symposia in PureMathematics,1990, 51:187-194. [3]Semrl P.Local automophis ms and derivations on[J].Proc Amer.Math.Soc.,1997,125:2677-2680. [4]BresarM,Semrl P.Mappingswhich preserve idempotents,local automorphis ms,and local derivation[J].Canad Math,1993, 45:483-496. [5]Crist R L.Local derivation on operator algebras[J].Funct.Anal,1996,135:76-92. [6]Larson D R.Reflexivity,algebra reflexivity,and linear interpolation[J].Amer.Math,1988,110:283-229. [7]BresarM,VillenaA R.The noncommutative Singer-Wermer conjecture andφ-derivations[J].LondonMath.Soc,2002,66: 710-720. [8]Bergen J.Skew derivationswhose invariants satisfy a polynomial identity[J].Algebra,2000,228:710-737. [9]Chuang C L.Identitieswith skew derivations[J].Algebra,2000,224:292-335. [10]Chuang C L,Lee T K.Algebraic-skew derivations[J].Algebra,2004,282:1-22. [11]Chuang C L,Lee T K.Identitieswith a single skew derivation[J].Algebra,2005,288:59-77. [12]BresarM,Fosner A,FosnerM.A Kleinecke-Shirokov type condition with Jordan automorphisms[J].Studia Math,2001, 147:237-242. 2-Local Skew-Derivation of Nest Algebras WU Rui-hua,LüChuan (School ofMathematics and Computational Science,China University of Petroleum,Dongying Shandong 257061,China) A study on the 2-localφ-derivation of nest algebras is made by using the characteristics of the concepts and mappings of algebras.It is proved that every 2-localφ-derivation of nest algebras is aφ-derivation. 2-localφ-derivation;φ-derivation;nest algebra book=5,ebook=383 O 177.1 A 1673-2103(2010)05-0005-04 2010-07-18 中國石油大學自主創新科研計劃項目(09CX04065A) 吳瑞華(1981-),女,山東臨沂人,講師,碩士,研究方向:算子理論與算子代數.1 預備知識
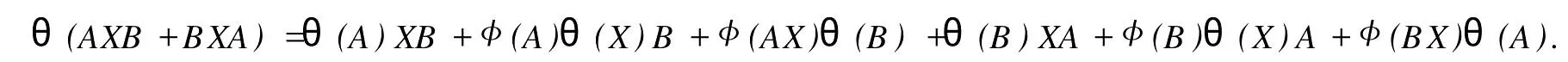
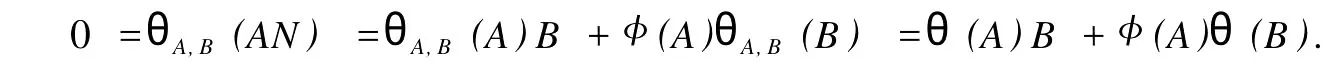
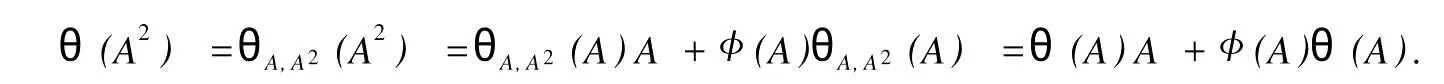
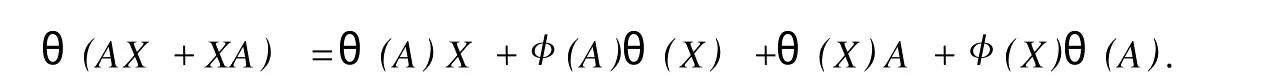
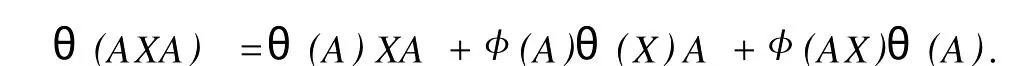
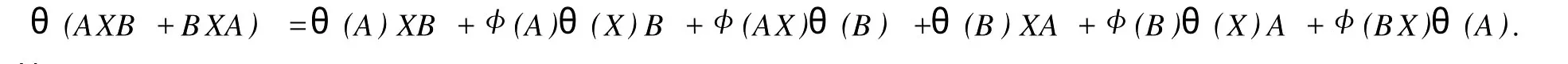
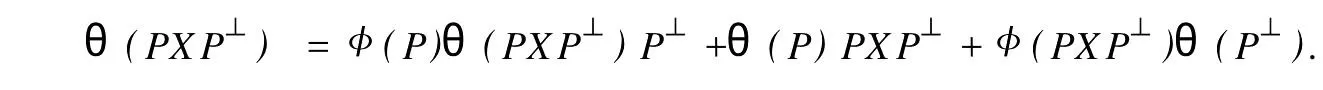
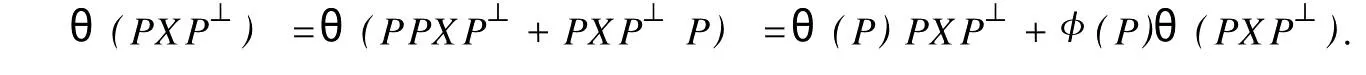
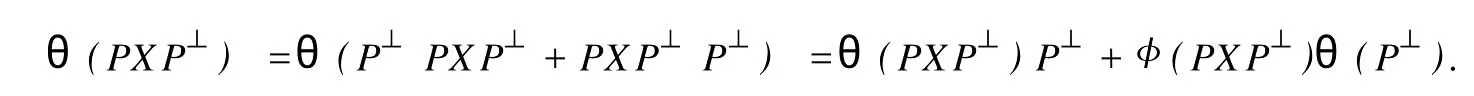

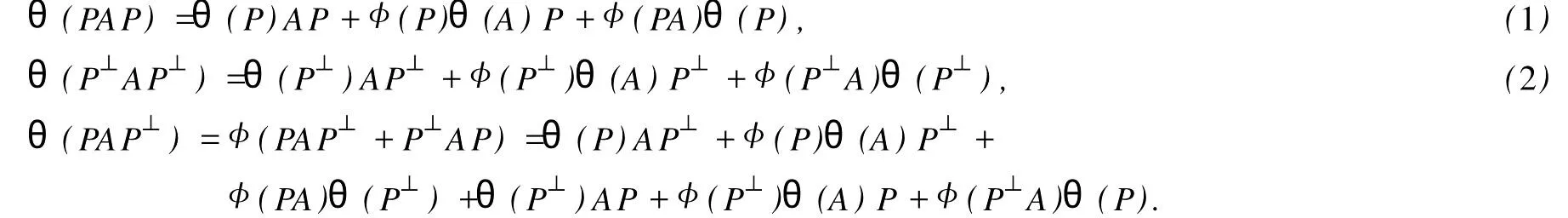
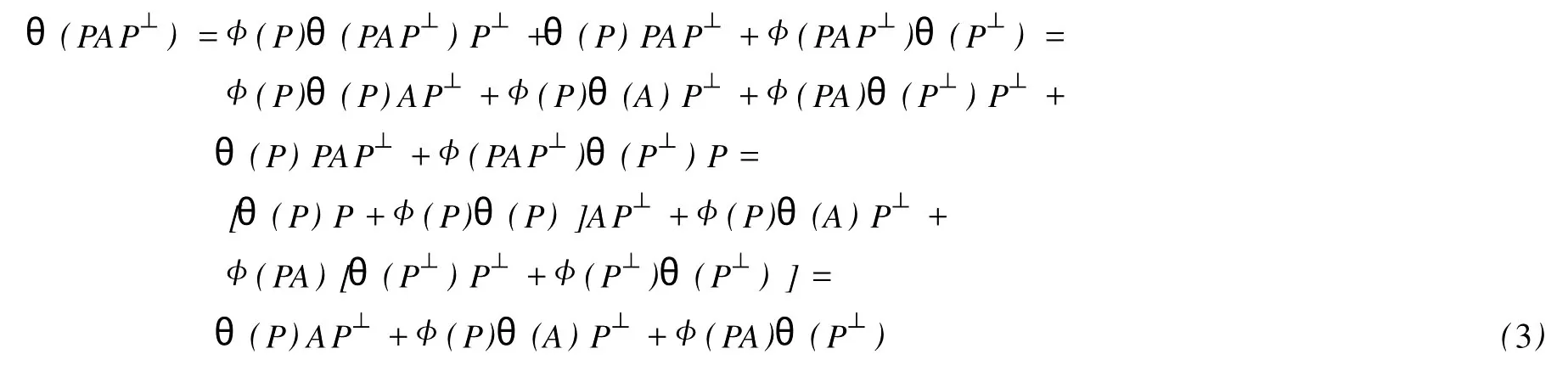
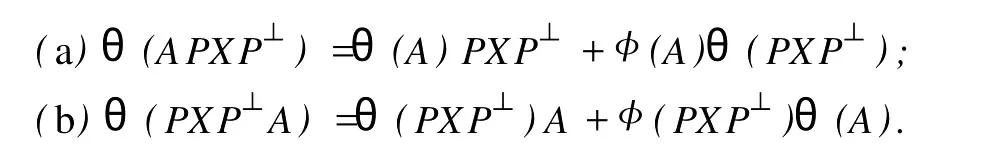
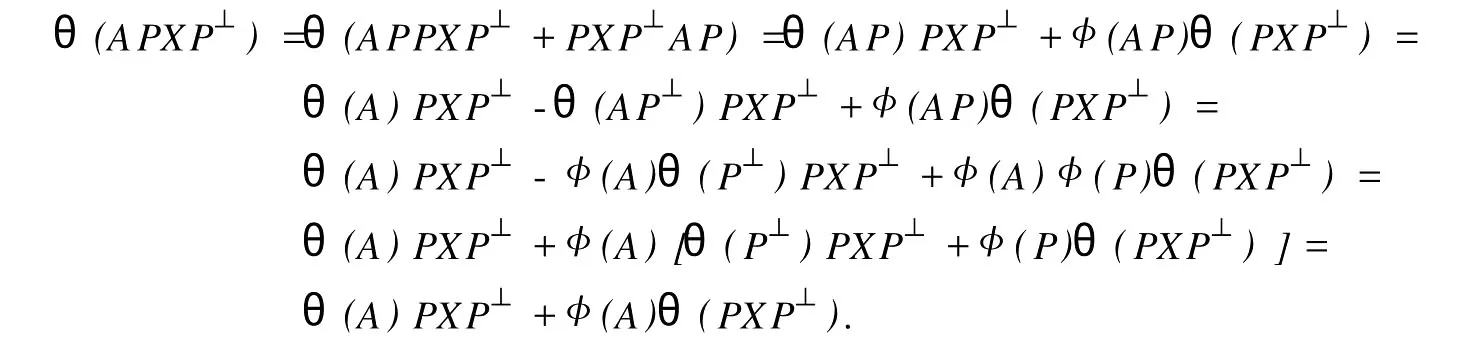
2 主要結果