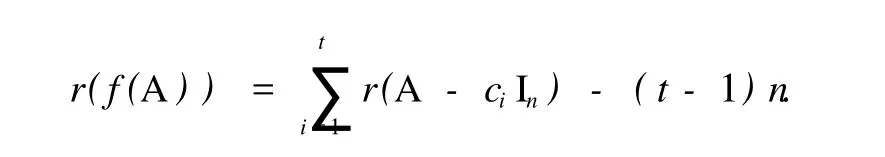關于矩陣多項式秩的幾個恒等式＊

宋小力

(青島酒店管理職業技術學院基礎部,山東青島 266071）

關于矩陣多項式秩的幾個恒等式＊

宋小力

(青島酒店管理職業技術學院基礎部,山東青島 266071）

矩陣運算的秩一般以不等式的形式出現,給矩陣秩的計算和應用造成諸多不便.利用互素多項式乘積秩的恒等式以及方陣冪秩的分塊矩陣表示,給出了一般矩陣多項式秩的分塊矩陣表示以及在矩陣可以對角化情況下的一個恒等式.

矩陣;秩;多項式

引言

秩是矩陣的一個重要而應用廣泛的數值特征.在矩陣論中,矩陣秩的結果多以不等式形式出現,給矩陣秩的進一步應用造成諸多不便.因此,對矩陣秩恒等式的構造和研究是矩陣論中的一個基本問題.文獻[1]將矩陣乘積秩的 Sylvester不等式的推廣形式中的矩陣進行限定,給出了 A+kiIn型矩陣乘積秩與矩陣秩和的一些恒等式結果,并提出了下列猜想:設,A∈Fn×n,k1,k2,…,kt∈F.當 k1,k2,…,kt滿足適當條件時,則

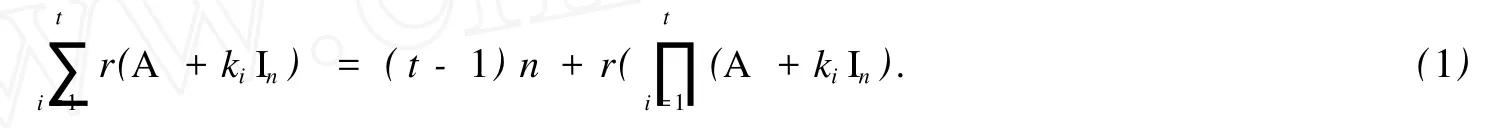
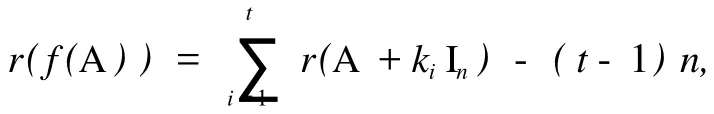
1 預備知識

在本文的討論中,主要應用下面的兩個引理.

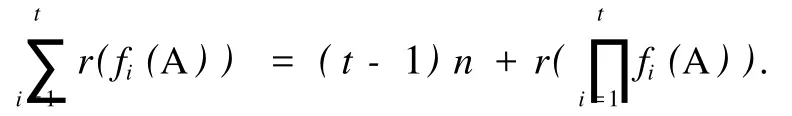
引理 2[4]設 A∈Fn×n.則對任意正整數 k,有

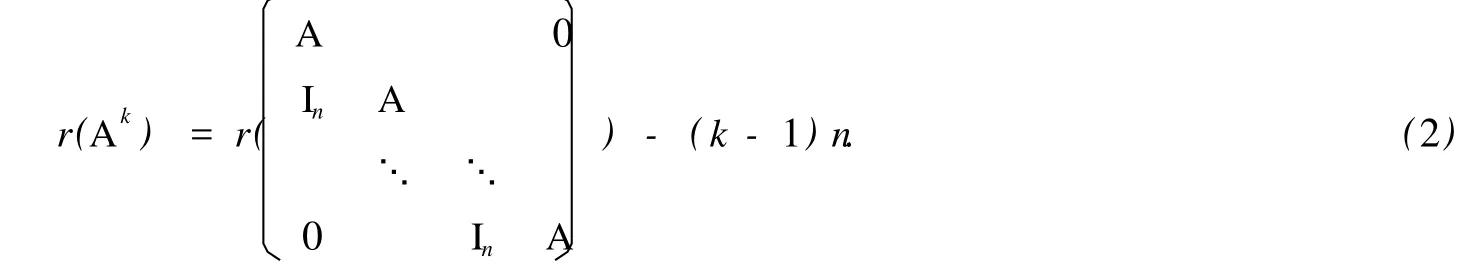
式中分塊矩陣的主對角線上有 k個 A.

2 主要定理及證明

定理 1 設 f(x)是數域 F上的 m(m>0)次多項式,c1,c2,…,ct是 f(x)的所有互異復根,重數分別為 s1,s2,…,st.則對任意 n階方陣 A,下列矩陣多項式秩恒等式成立:

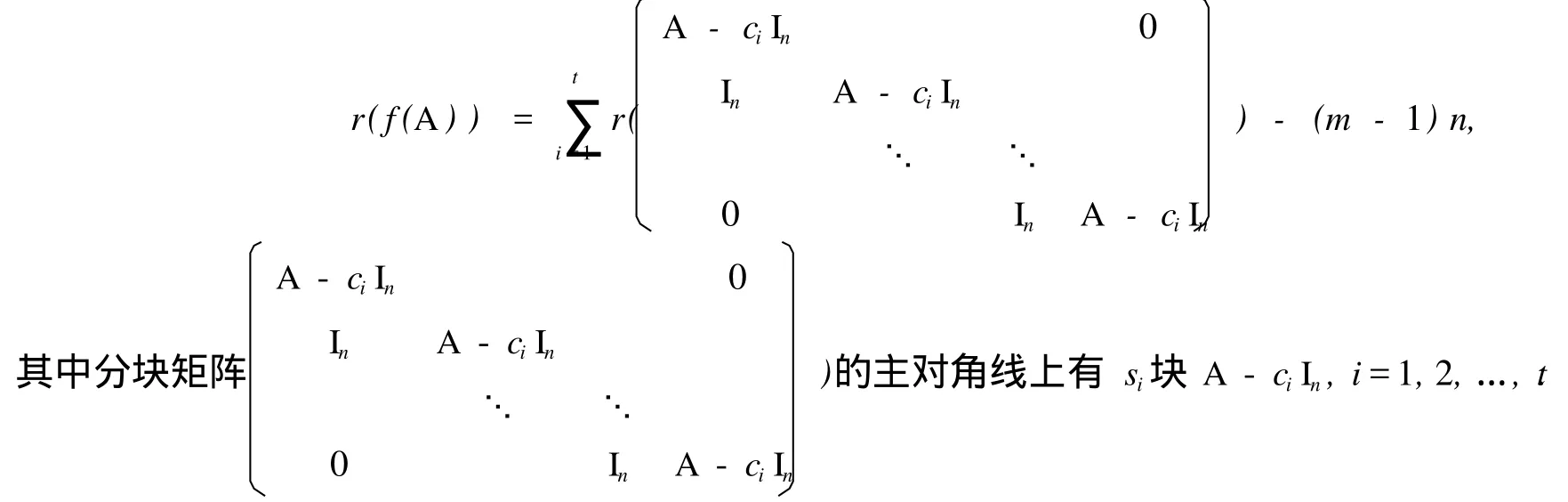
證明 由條件可設 f(x)在復數域上的典型分解式為 f(x)=a(x-c1)s1(x-c1)s2…,(x-c1)st,其中 a≠0是 f(x)的首項系數.由 c1,c2,…,ct互異,則 (x-c1,x-c2,…,x-ct)=1,故 ((x-c1)s1,(x-c1)s2,…,(xct)st)=1.

故由引理 1得

故結論成立.

推論 設 A,B為任意的 n階方陣,令φA(x),φB(x)分別為 A,B的特征多項式且 (φA(x),φB(x))=d(x),則 r(φA(B))=r(d(B)),r(φB(A))=r(d(A)).

證明 由φA(A)=0,φB(B)=0以及矩陣秩的基本性質可得.

對數域 F上的 m(m>0)次多項式 f(x)以及 n階方陣 A,若 m≥n,令φA(x)=|xIn-A|為 A的特征多項式并與 f(x)進行帶余除法,即設 f(x)=q(x)φA(x)+k(x),其中 k(x)=0或 degk(x)

定理 2 設 f(x)是數域 F上的 m(m>0)次多項式,c1,c2,…,ct是 f(x)的所有互異復根,(f(x),f′(x))=d(x).對任意 n階方陣 A,若 d(A)可逆,則下列矩陣多項式秩恒等式成立:

即結論成立.

當方陣 A可以對角化時,下列結論給出了 r(f(A))與A的某些特征根重數的關系式.

證明 由矩陣 A可以對角化,則存在 n階可逆矩陣 P,使

對多項式 f(x),由矩陣運算以及 (4)可得

由 Sf∩SA={λi1,λi2,…,λit},則當 ij∈{i1,i2,…,it}時 f(λij)=0,當 ij?{i1,i2,…,it}時 f(λij) ≠0.故

故結論成立.

[1]李書超,蔣君,向世斌,等.一類矩陣秩的恒等式及其推廣[J].武漢科技大學學報,2004,27(1):96-98.

[2]余世群.關于“一類矩陣秩的恒等式及其推廣”一文的注記[J].武漢科技學院學報,2006,19(10):28-29.

[3]宋小力.一類矩陣乘積秩的恒等式及應用[J].四川兵工學報,2010,31(3):135-137.

[4]王廷明.關于矩陣的和與乘積秩的分塊矩陣表示[J].棗莊學院學報,2003,20(5):33-36.

Several Identical Equations about the Ranks of theMatrix Polynom ials

SONG Xiao-li

(Basic Department ofVocational&Technical College,Qingdao HotelManagement,Qingdao Shandong 266071,China)

The ranks of matrix operations usually show the for ms of inequalities,which are inconvenient for calculation and application of the matrix ranks.However,the identical equations of the ranks of copr ime polynomials,aswell as the block matrix denotations of the square matrix’s power ranks,are both concerned in this paper.Then the expressions of the ranks of general matrix polynomials are obtained by virtue of block matrices.Meanwhile,an identical equation is also

under the conditions of diagonalizable matrices.

matrix;rank;polynomial

O 151.21

A

1673-2103(2010)05-0036-03

2010-07-20

宋小力 (1965-),女,山東青島人,副教授,研究方向:矩陣理論與應用.