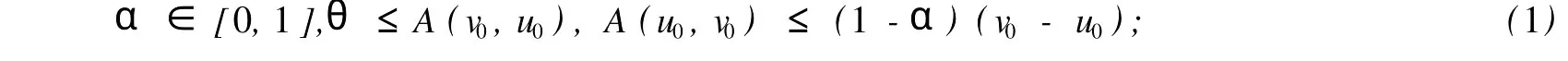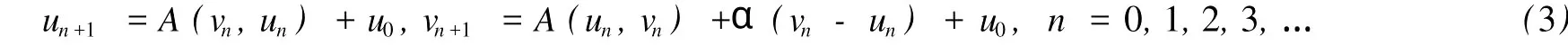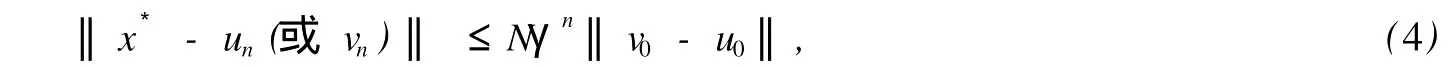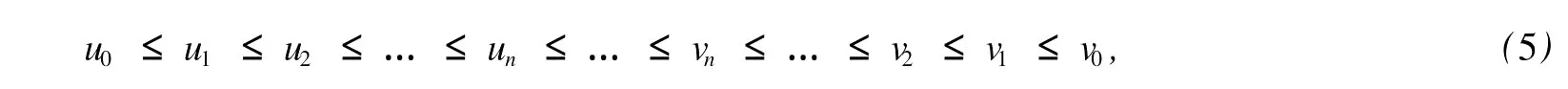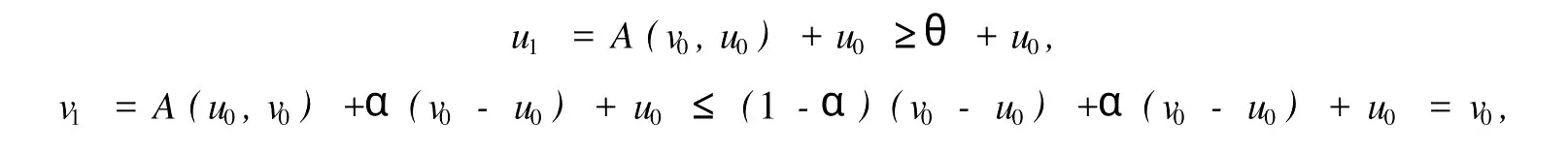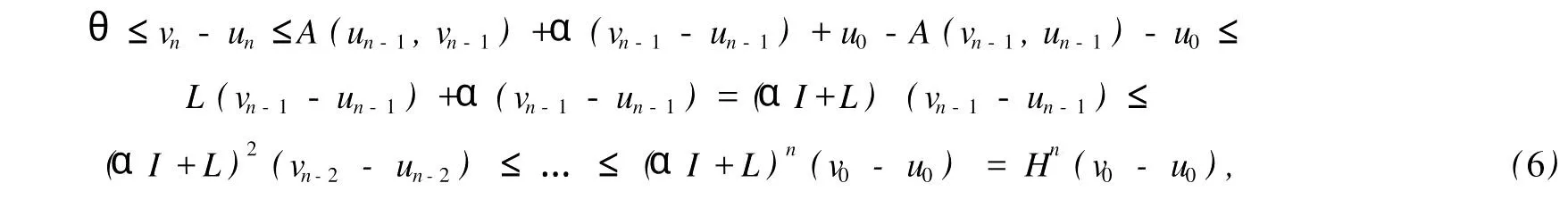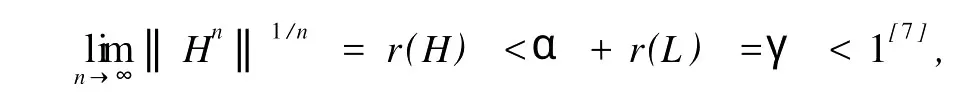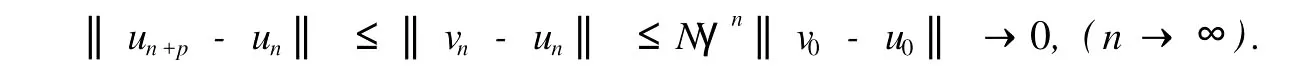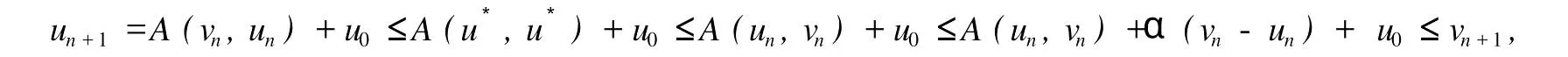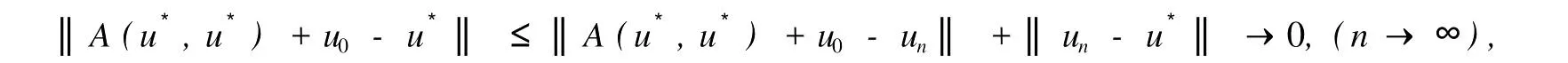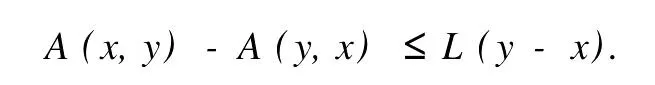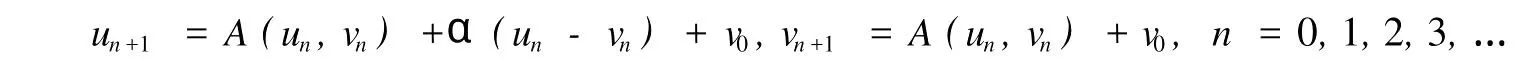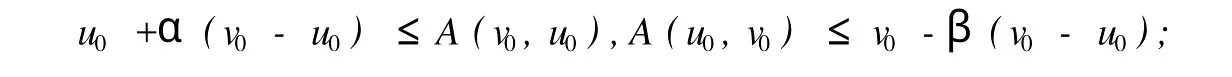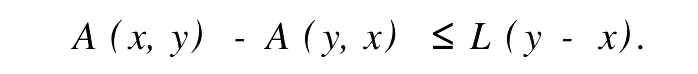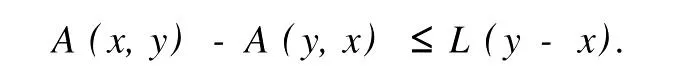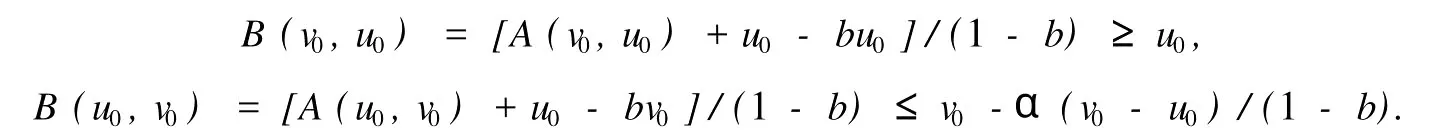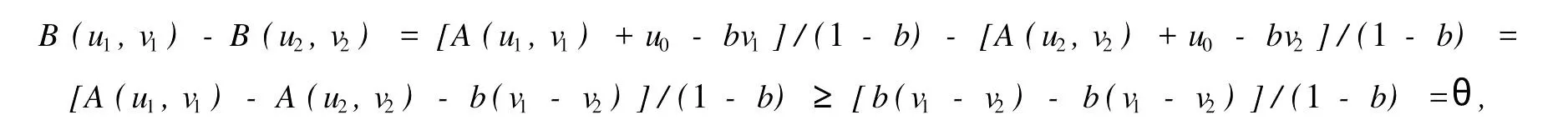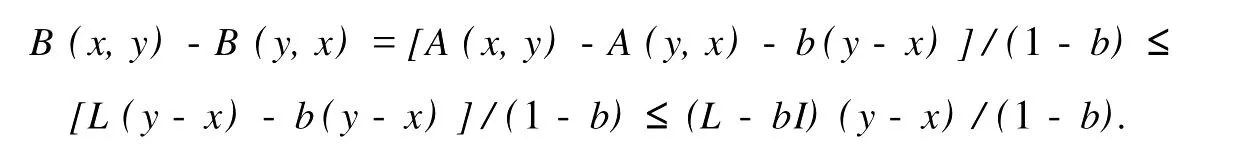一類不具有連續(xù)性和緊性條件的反向混合單調(diào)算子方程解的存在性定理＊

李慶芳

(河南化工職業(yè)學(xué)院公共課教學(xué)部,河南鄭州450042)

一類不具有連續(xù)性和緊性條件的反向混合單調(diào)算子方程解的存在性定理＊

李慶芳

(河南化工職業(yè)學(xué)院公共課教學(xué)部,河南鄭州450042)

在半序空間中,研究了不具有連續(xù)性和緊性條件的一類反向混合單調(diào)算子方程解的存在與惟一性,并給出迭代序列收斂于解的誤差估計(jì),所得結(jié)果是某些已有結(jié)果的本質(zhì)改進(jìn)和推廣.

正規(guī)錐;反向混合單調(diào)算子;算子方程;方程解

混合單調(diào)算子和反向混合單調(diào)算子是兩類重要的算子,關(guān)于Banach空間中非線性混合單調(diào)算子方程A(x,x)=x的迭代求解問題,已有許多研究[1～7],并得到了一批好的結(jié)果,但對(duì)于反向混合單調(diào)算子方程A(x,x)+u0=x解的存在性問題卻涉及甚少.本文利用了非對(duì)稱迭代法解決了半序空間中慣用的對(duì)稱迭代法所無能為力的問題,討論了反向混合單調(diào)算子方程A(x,x)+u0=x解的存在惟一性,并給出了迭代序列收斂于解的誤差估計(jì),改進(jìn)和推廣了已有文獻(xiàn)中的相應(yīng)結(jié)果.

1 預(yù)備知識(shí)

本文總假設(shè)E為具有正規(guī)錐P的半序?qū)岯anach空間,θ表示E中的零元素,N為P的正規(guī)常數(shù),關(guān)于錐和半序理論參見文獻(xiàn)[8].設(shè)u0,v0∈E且u0

定義1[1]稱二元算子A:D×D→E為混合單調(diào)算子,如果A(x,y)對(duì)每一個(gè)固定的y∈D關(guān)于x是增的,對(duì)每一個(gè)固定的x∈D關(guān)于y是減的.

定義2[8,9]稱二元算子B:D×D→E為反向混合單調(diào)算子,若:

1)對(duì)每個(gè)固定的v∈D,B(u,v)在D上關(guān)于u是單調(diào)遞減的,即?u1

2)對(duì)每個(gè)固定的u∈D,B(u,v)在D上關(guān)于v是單調(diào)遞增的,即?v1

2 主要結(jié)果

定理1 設(shè)P是實(shí)Banach空間E中正規(guī)錐,A:D×D→E是反向混合單調(diào)算子,且滿足: 1)存在

2)存在正有界線性算子L:E×E→E且其譜半徑r(L)<1,使得對(duì)任意的x,y∈D,x≤y有

則當(dāng)0<α+r(L)<1時(shí),方程A(x,x)+u0=x在[u0,v0]中有惟一解且對(duì)迭代序列

有誤差估計(jì)式中γ=α+r(L).

證明 運(yùn)用歸納法易證

事實(shí)上,當(dāng)n=1時(shí),由式(1)、(2)及A是反向混合單調(diào)算子,我們有

v1-u1=A(u0,v0)-A(v0,u0)+α(v0-u0)≥θ,即u0≤u1≤v1≤v0,式(5)成立.

假設(shè)n=k時(shí),式(5)也成立,即uk-1≤uk≤vk≤vk-1,則當(dāng)n=k+1時(shí),有

即 uk≤uk+1≤vk+1≤vk,故n=k+1時(shí)式(5)成立.

由式(2)、(3)和(5)可得

式中H=αI+L,I是恒等算子,對(duì)任給的0

存在n0,使得‖Hn‖<γn,n≥n0,考慮到P的正規(guī)性知

故由式(6)知,對(duì)任意正數(shù)n,p有θ≤un+p-un,vn-vn+p≤vn-un≤Hn(v0-u0),

從而由式(7)與P的正規(guī)性知

所以{un}是Cauchy序列,由E的完備性及{un}∈[u0,v0],存在

同理可證{vn}也是Cauchy序列.于是存在

又由式(3)、(8)及A是反向混合單調(diào)算子有

可得

故有

即x＊是方程A(x,x)+u0=x在[u0,v0]中的解.

再證不動(dòng)點(diǎn)的惟一性:設(shè)y＊也是A在[u0,v0]中的不動(dòng)點(diǎn),則仿上述證明由歸納法易得令 n→∞得是方程A(x,x)+u0=x在[u0,v0]中的惟一解.

誤差估計(jì)式(4)由式(7)易得.

定理2 設(shè)P是實(shí)Banach空間E中正規(guī)錐,A:D×D→E是反向混合單調(diào)算子,且滿足:

1)存在α∈[0,1],(1-α)(u0-v0)≤A(v0,u0),A(u0,v0)≤θ;

2)存在正有界線性算子L:E×E→E且其譜半徑r(L)<1,使得對(duì)任意的x,y∈D,x≤y,有

則當(dāng)0<α+r(L)<1時(shí),方程A(x,x)+v0=x在[u0,v0]中有惟一解有誤差估計(jì)

證明 類似于定理1的證明,略.

定理3 設(shè)P是實(shí)Banach空間E中正規(guī)錐,A:D×D→E是反向混合單調(diào)算子,且滿足:

1)存在α∈[0,1],∈[0,1],有

2)存在正有界線性算子L:E×E→E且其譜半徑r(L)<1,使得對(duì)任意的x,y∈D,x≤y有

則當(dāng)0<α+β+r(L)<1時(shí),方程A(x,x)=x在[u0,v0]中有惟一解且對(duì)迭代序列有誤差估計(jì)其中γ=α+β+r(L).

下面討論A未必反向混合單調(diào)時(shí)的一些結(jié)論.

定理4 設(shè)P是實(shí)Banach空間E中正規(guī)錐,A:D×D→E是二元算子,且滿足:

1)若存在α∈[0,1],滿足初始條件θ≤A(v0,u0),A(u0,v0)≤(1-α)(v0-u0);

2)存在b>0,使得b(y1-y2)≤A(x1,y1)-A(x2,y2),u0≤x1≤x2≤v0,u0≤y2≤y1≤v0;

3)存在正有界線性算子L:E×E→E且其譜半徑r(L)<1,使得對(duì)任意的x,y∈D,x≤y有

則當(dāng)0<[α+r(L)-b]/(1-b)<1時(shí),方程A(x,x)

證明 令B(x,y)=[A(x,y)+u0-by]/(1-b),x,y∈D.由1)知,

又由2)知,對(duì)任給的ui,vi∈D,(i=1,2),當(dāng)u2≥u1,v2≤v1時(shí),

所以B(u1,v1)≥B(u2,v2),即B:D×D→E是反向混合單調(diào)算子.

再由3)知,

構(gòu)造迭代序列un+1=B(vn,un),vn+1=B(un,vn)+α(vn-un)/(1-b),則仿文獻(xiàn)[6]中定理的證明可得B(x,x)=x在D中有惟一解(1-b)的惟一解.仿上證明可得下面結(jié)論.

定理5 設(shè)P是實(shí)Banach空間E中正規(guī)錐,A:D×D→E是二元算子,且滿足:

1)存在α∈[0,1],滿足初始條件(1-α)(u0-v0)≤A(v0,u0),A(u0,v0)≤θ;

2)存在b>0,使得b(y1-y2)≤A(x1,y1)-A(x2,y2),u0≤x1≤x2≤v0,u0≤y2≤y1≤v0;

3)存在正有界線性算子L:E×E→E且其譜半徑r(L)<1,使得對(duì)任意的x,y∈D,x≤y有

則當(dāng)0<[α+r(L)-b]/(1-b)<1時(shí),方程A(x,x)+v0=x在[u0,v0]中有惟一解x＊.

注1 本文定理4,5中研究了算子A未必反向混合單調(diào)時(shí)仍有相應(yīng)的結(jié)論,拓寬了定理的適用范圍.

注2 本文結(jié)論對(duì)算子A在連續(xù)性和緊性方面沒有作任何假定.

[1]Guo Dajun,Lakshmikantham V.Coupled fixed points of nonlinear operators with applications[J].Nonlinear Anal T MA,1987,11 (5):623-632.

[2]顏心力.對(duì)稱壓縮算子方程解的存在惟一性定理及其應(yīng)用[J].科學(xué)通報(bào),1990,35(10):733-736.

[3]張慶政.序?qū)ΨQ壓縮算子方程的迭代求解及其應(yīng)用[J].工程數(shù)學(xué)學(xué)報(bào),2000,17(2):131-134.

[4]徐裕生,孫俊萍.一類混合單調(diào)算子方程解的存在惟一性定理[J].陜西師大學(xué)報(bào),2002,30(3):1-4.

[5]孫義靜.一類非線性算子方程組的迭代算法及應(yīng)用[J].浙江大學(xué)學(xué)報(bào),1999,33(3):289-294.

[6]李俊強(qiáng),張斐然.一類混合單調(diào)算子的新不動(dòng)點(diǎn)定理的推廣[J].鄭州大學(xué)學(xué)報(bào),2004,36(4):13-15.

[7]TaylorA E,LayD C.Introduction to FunctionalAnalysis[M].New York:spinger-verlag,1980;277-281.

[8]郭大鈞.非線性泛函分析[M].濟(jì)南:山東科技出版社,1985.

[9]欒世霞,孫欽福,趙艷玲.反向混合單調(diào)算子新的不動(dòng)點(diǎn)定理[J].吉首大學(xué)學(xué)報(bào),2008,29(1):7-9.

Existence Theorem of Solution of Anti-m ixedMonotone Operator Equation without the Conditions of Cont inuity and Compactness

LIQing-fang

(Dept.of Public Courses,Henan Vocational College of Chemical Technology,Zhengzhou Henan 450042,China)

The paper discusses the existence and uniqueness of solution of anti-mixed monotone operator equation in semi-ordered space without the conditions of continuity and compactness,and the error estimations that iterative sequences converge to solutions are given.The results presented here improve and generalize some correspondingresults for anti-mixed monotone operators.

normal cone;anti-mixed monotone operator;operator equation;equation solution

book=9,ebook=375

O 177.91

A

1673-2103(2010)05-0032-04

2010-06-11

河南省教委科研基金資助項(xiàng)目(200810483004)

李慶芳(1973-),女,河南鄭州人,講師,研究方向:非線性泛函分析及其應(yīng)用.