凸函數(shù)定義等價(jià)性的進(jìn)一步探討
張 金
(宿遷高等師范學(xué)校 數(shù)學(xué)系,江蘇 宿遷 223800)
0 引言
凸函數(shù)是一重要的概念。 已有的文獻(xiàn)中,在給定的區(qū)間I上,給出了凸函數(shù)多種不同形式的定義,并對(duì)定義之間等價(jià)性作了分析與證明,見(jiàn)文獻(xiàn)[1]~[5]。 下文擬對(duì)一般區(qū)間I上的凸函數(shù)最基本的定義作一概述,進(jìn)一步探討與證明它們之間的等價(jià)性。
1 凸函數(shù)的基本定義
下面給出凸函數(shù)幾種定義:
定義1 :設(shè)函數(shù)f(x)在區(qū)間I上有定義,f(x)稱(chēng)為I上的凸函數(shù),當(dāng)且僅當(dāng):?x1,x2∈I,有
(1)
定義2 :設(shè)函數(shù)f(x)在區(qū)間I上有定義,f(x)稱(chēng)為I上的凸函數(shù),當(dāng)且僅當(dāng):?x1,x2,…,xn∈I,有
(2)
定義3[6]:設(shè)函數(shù)f(x)在區(qū)間I上有定義,f(x)稱(chēng)為I上的凸函數(shù),當(dāng)且僅當(dāng):?x1,x2∈I,?λ∈(0,1),有
f(λx1+(1-λ)x2)≤λf(x1)+(1-λ)f(x2)
(3)
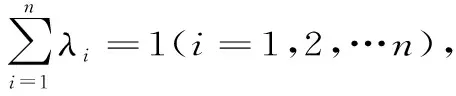
(4)
定義5 :設(shè)函數(shù)f(x)在區(qū)間I上有定義,f(x)稱(chēng)為I上的凸函數(shù),當(dāng)且僅當(dāng):
?pi≥(i=1,2,…n)不全為零,?x1,x2,…xn∈I,有
(5)
定義6 :設(shè)函數(shù)f(x)在區(qū)間I上有定義,f(x)稱(chēng)為I上的凸函數(shù),當(dāng)且僅當(dāng):?x1,x2,…xn∈I,且x1 (6) 定義7 :設(shè)函數(shù)f(x)在區(qū)間I上有定義,f(x)稱(chēng)為I上的凸函數(shù),當(dāng)且僅當(dāng):?x1,x2,…xn∈I,且x1 (7) 上述定義中的“≤”若改為“<”,則得f(x)為I上的嚴(yán)格凸函數(shù)。 區(qū)間I上可導(dǎo)或二階可導(dǎo)的凸函數(shù)還可借助導(dǎo)數(shù)f′(x)的單調(diào)遞增或f″(x)來(lái)判定或定義(見(jiàn)文獻(xiàn)[1][2][3]),這一點(diǎn)本文不再贅述。 首先給出幾個(gè)定理: 定理1 :定義1與定義2等價(jià)。 證明 :“定義2?定義1”顯然成立,在(2)式中令n=2即得(1)式。 只要證明:“定義1?定義2”。采用反向歸納法。 1)由(1)式知:當(dāng)n=2時(shí)(2)式成立。 現(xiàn)證n=4時(shí)(2)式成立。 事實(shí)上,?x1,x2,x3,x4,∈I,由(1)式有 此即(2)式當(dāng)n=4時(shí)成立。 一般地,對(duì)任一正整數(shù)k,重復(fù)上面方法,應(yīng)用(1)式k次,可知 這表明(2)式對(duì)一切n=2k皆成立。 此即(2)式對(duì)n=k也成立。 證畢。 下面給出關(guān)于凸函數(shù)的一個(gè)論斷,以引理1命名: 引理1:若函數(shù)f(x)為區(qū)間I上的凸函數(shù),則f(x)在I內(nèi)部任意一點(diǎn)都連續(xù)。 定理2 :定義3與定義1,2等價(jià)。 對(duì)于有理數(shù)λn∈(0,1),利用上面證明有 f(λnx1+(1-λn)x2)≤λnf(x1)+(1-λn)f(x2) 此式中令n→∞取極限并聯(lián)系上式,有 f(λx1+(1-λ)x2)≤λf(x1)+(1-λ)f(x2) 此即(3)式對(duì)任意無(wú)理數(shù)λ∈(0,1)也成立。 故定義1,2也蘊(yùn)含定義3,證畢。 定理3 :定義3與定義4,5等價(jià)。 證明 “定義4?定義3”只要在(4)式中令n=2即得。“定義3?定義4”采用數(shù)學(xué)歸納法可證(定義4即為“Jensen不等式”,證明見(jiàn)文獻(xiàn)[6])。“定義4?定義5”明顯,故定理3得證。 定理4:定義3與定義6,7等價(jià)。 f(λx3+(1-λ)x1)≤λf(x3)+(1-λ)f(x1) 即 此式化簡(jiǎn)變得(6)式,故“定義3?定義6”成立。 反之?λ∈(0,1),?x1,x2∈I,,不妨設(shè)x1 由上述定理可知上文所給的凸函數(shù)幾個(gè)基本定義是等價(jià)的, 區(qū)別僅是呈現(xiàn)的形式或各自的幾何意義有所不同,但均是對(duì)凸函數(shù)本質(zhì)的概述。 定義或概念是對(duì)事物本質(zhì)屬性的精確概括。 具體教學(xué)中,強(qiáng)調(diào)學(xué)生對(duì)概念的理解,目的就在于希望學(xué)生能夠抓住事物的本質(zhì)屬性。 定義3更能體現(xiàn)凸函數(shù)的本質(zhì)屬性,其幾何意義對(duì)凸函數(shù)描述很直觀(guān),現(xiàn)代數(shù)學(xué)中多采用這種定義。 值得一提的是,區(qū)間I上的凸函數(shù)的“凸”性?xún)H由區(qū)間I內(nèi)部函數(shù)的屬性來(lái)體現(xiàn),而與函數(shù)在區(qū)間端點(diǎn)的取值無(wú)關(guān)。 文中引理表明,在區(qū)間I內(nèi)部凸函數(shù)是連續(xù)的,對(duì)應(yīng)的曲線(xiàn)是連續(xù)曲線(xiàn)且呈“下凸”趨勢(shì)。 同時(shí)也表明,凸函數(shù)的間斷點(diǎn)只可能出現(xiàn)在區(qū)間的端點(diǎn)上。 [參考文獻(xiàn)] [1] 王飛.凸函數(shù)等價(jià)性討論[J].廣西師范學(xué)院學(xué)報(bào):自然科學(xué)版,2003,20(1):31-34. [2] 趙丹.凸函數(shù)等義的等價(jià)性證明[J].樂(lè)山師范學(xué)院學(xué)報(bào),2008,23(12):18-21. [3] 古小敏.對(duì)凸函數(shù)定義之間等價(jià)性的進(jìn)一步研究[J].重慶工商大學(xué)學(xué)報(bào):自然科學(xué)版,2009,26(2):171-173. [4] 郭素霞.關(guān)于凸函數(shù)定義的討論[J].衡水師專(zhuān)學(xué)報(bào),2000,2(4):49-52. [5] 黃世團(tuán).幾個(gè)凸函數(shù)定義的差異性及等價(jià)性[J].廣西師院學(xué)報(bào):自然科學(xué)版,1997,14(1):54-56. [6] 華東師范大學(xué)數(shù)學(xué)系. 數(shù)學(xué)分析:上冊(cè) [M].2版.北京:高等教育出版社,1991:197-203.2 定義之間等價(jià)性的證明與探討
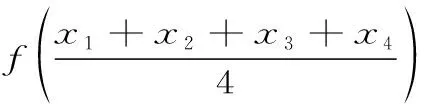
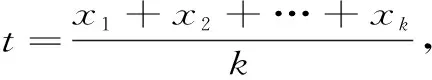
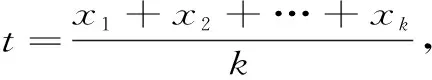

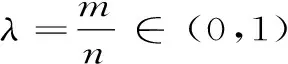
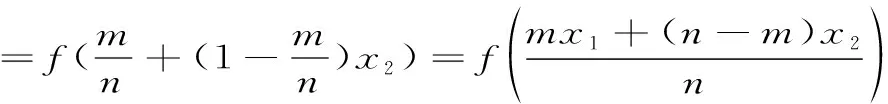
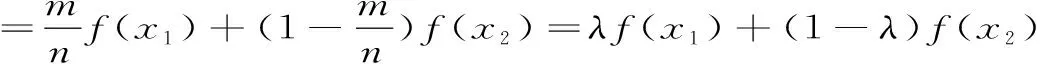
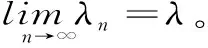

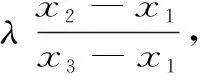
3 結(jié)束語(yǔ)
 大慶師范學(xué)院學(xué)報(bào)2010年6期
大慶師范學(xué)院學(xué)報(bào)2010年6期
——以第41屆世界體操錦標(biāo)賽為例
