關于無窮級數求和的研究及應用

陳文生

(宿遷高等師范學校 數學系，江蘇 宿遷 223800)

1 引言及預備知識

無窮級數的斂散性以及求和是高等數學中一個重要而有趣的研究課題，長期以來備受人們的關注。 很多學者做了大量工作，對某些具有特殊通項表達式的無窮級數的斂散性或求和總結出一些規律性的解法(見文獻[1]-[4])。 本文從無窮級數部分和的子序列的角度，把級數求和的問題轉化數列極限的計算問題，給出了一種判斷級數斂散性的方法，并且給出了這種方法在無窮級數求和以及判斷級數斂散性中的某些應用。

數列{Sn}的斂散性可由其子列來研究，并且有一個重要的結論。

引理1[5]：數列{Sn}收斂的充分必要條件是{Sn}的任一子列都收斂，且有相同的極限。

特別地，由引理1，可得

引理2： 數列{Sn}收斂于S的充分必要條件是{Sn}的兩個子列{S2n}和{S2n-1}都收斂于同一極限。

此時，稱兩個子列{S2n}和{S2n-1}為互補子序列。

可將引理2推廣到一般情形。

定理1： 數列{Sn}收斂于S的充分必要條件是{Sn}的p(p是某個正整數)個子列{Spn}，{Spn-1}，…{Spn-(p-1)}都收斂于同一極限S。

證明 當p=1，p=2時，結論顯然成立；下面證明當p=3時結論成立，其他情形類似可證。 由引理1可知“必要性”顯然，只要證明“充分性”。 由條件，{Sn}的3個子列{S3n}，{S3n-1}， {S3n-2}都收斂于同一極限S，于是，由數列收斂的“ε-N”定義可得，對任意的ε>0，存在一個充分大的正數N>0，當n>N時，此時n=3k或n=3k-1或n=3k-2，從而有|S-Sn|<ε，故證得數列{Sn}收斂于S。

2 主要結果

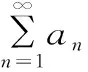
進一步，可將定理2推廣到一般情形：

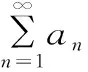
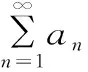
3 結論應用

本小節我們給出子序列方法在無窮級數求和以及判斷級數斂散性中的某些應用。

(1)

其中C=0.577216…稱為Euler常數，且εn→0(當n→∞時)。對于原級數，并由(1)式可知

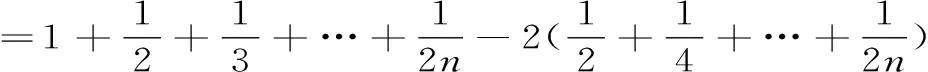
=C+ln2n+ε2n-C-CLNN-εn

=ln2+ε2n-εn→n2(當n→∞時)。

所以，由定理3知，原級數收斂，其和為S=ln2。

例2： 計算

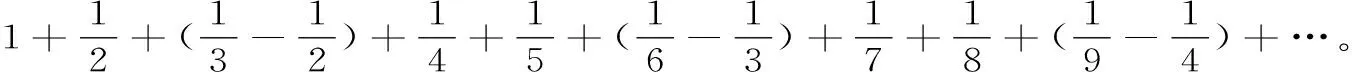
解： 易知此級數通項an→0(當n→∞時)，觀察原級數后，考察部分和數列的子列{S3n}的極限。對于原級數，并由(1)式可知

=C+ln3n+ε3n-(C+ln(n+1)+εn-1)→ln3+1(當n→∞時)。

所以，由定理3知，原級數收斂，其和為S=ln3+1。

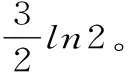
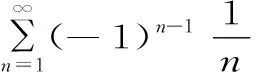
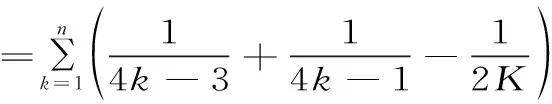
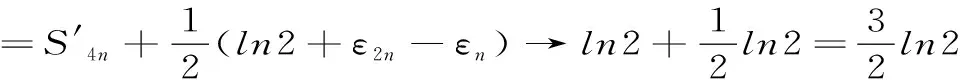
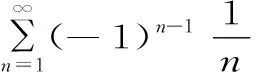
例4： 證明調和級數

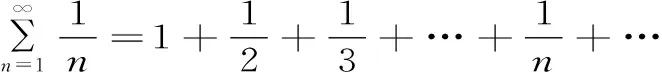
證明： 考察調和級數的部分和數列{Sn}(此時p=1)，并由(1)式知

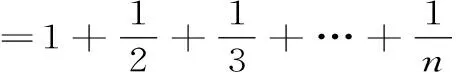
=C+lnn+εn→+∞(當n→∞時，并注意到lnnn→+∞)

故調和級數發散。

例5： 證明級數

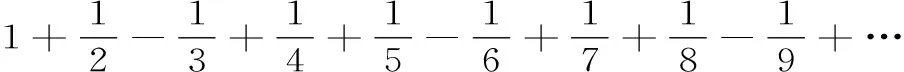
證明： 雖然此級數的通項an→0(當n→∞時)，但它的部分和數列的一個子列{S3n}是發散的。

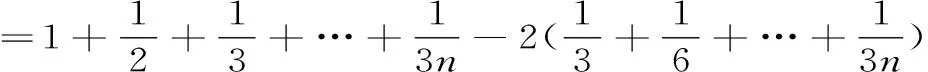
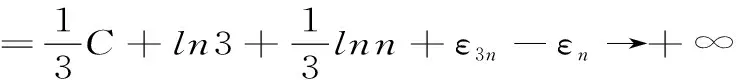
故原級數發散。

通過上述幾例我們可以看到，本文所給的子序列方法不僅能夠判定級數斂散性，而且能進一步求出一些特殊無窮級數的和。 與現有常用的級數斂散判別法相比，在某些情況下這種方法則更具有優越性。 這是因為，子序列方法是從收斂級數的部分和數列的角度，把級數求和的問題轉化為我們所熟知的數列極限的計算問題的。 應該說它是對現有方法的一個很好的補充。

[參考文獻]

[1] Bart Braden.Calculating sums of infinite series[J]. Amer. Math. Monthly,1992,99(7):649-655.

[2] Boas R. P.. Partial sums of infinite series and how they grow[J]. Amer. Math. Monthly, 1977, 84:237-258.

[3] 孫珍，李壽貴，張愛麗. 關于無窮級數求和的研究[J]. 數學雜志，2009，29(4)：490-292.

[4] 朱文輝，張亭. P級數的求和[J]. 大學數學，2005，21(3)：114-116.

[5] 華東師范大學數學系. 數學分析:上冊[M].2版. 北京：高等教育出版社，1991：43.

[6] 裴禮文. 數學分析中的典型問題與方法[M].北京：高等教育出版社，1993：19-20，338-340.