輔助函數法在一些數學問題中的應用

王利霞

（蘇州高等職業技術學校，江蘇 蘇州 215011）

輔助函數法在一些數學問題中的應用

王利霞

（蘇州高等職業技術學校，江蘇 蘇州 215011）

輔助函數法是處理和解決數學問題的一種重要思想方法。在高等數學解題中，往往不是直接對問題本身進行求解，而是根據問題以及所給的已知條件，巧妙地構造一個適當的輔助函數，從而間接有效的解決問題。

輔助函數法；極限；零值定理；羅爾定理

一、輔助函數在求極限中的應用

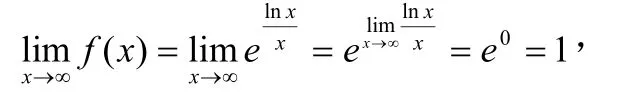
思路總結：構造恰當的輔助函數；化離散變量為連續變量，而且還必須考慮連續變量相應的極限過程（x→0或 x→+∞），如本例中用羅必達法則的過程；求解的關鍵在于考慮輔助函數極限的求得。

二、輔助函數在證明不等式中的應用

有關解不等式的問題，一般是運用比較法、分析法、綜合法等。然而，運算很麻煩，且不易得到結果。這時，若針對所解決的問題構造一個輔助函數，則原來問題的求解或證明，就轉化為對這一函數性質的研究，可以運用函數的定義域、值域、單調性、最值、連續和微積分等性質來幫助解決，運算過程就比較簡單了。

思路總結：（1）利用作商法比較；（2）構造恰當的輔助函數；（3）充分利用對數的性質求解。

三、輔助函數在證明等式中的應用

微分中值定理是數學分析的基礎之一,它的重要性是不言而喻的。所以很多證明題就是考察能否靈活運用中值定理。而在中值定理的應用中又以羅爾定理的應用居多。下面先介紹兩個定理：

零值定理：設函數 f( x)在閉區間[a,b]上連續，且f( a)· f( b) ＜ 0，則必存在 ξ∈ (a, b)使f(ξ)=0成立。這是介值定理的一種特殊情況。

羅爾定理：若函數f( x)在有限閉區間[a,b]上連續,在(a, b)上可導,并且 f( a) =f( b),則必 ?ξ∈ (a, b),使得f′(ξ) = 0.

例3 設f( x)在[a,b]上連續，且 a ＜c＜d ＜b，證明：在 (a,b)內 至 少 ? 一 個 ξ ， 使 得pf (c)+qf(d)=(p +q)f(ξ)，其中p，q為任意正常數。

證明 構造輔助函數F(x)=(p+q)f(x)-pf(c)-qf(d)，由題設可知F(x)在[a,b]上連續。

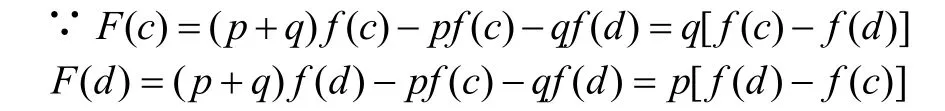
∴當 f(c)-f(d )≠0時，又 p＞0,q＞0，于是有F(c)F(d)=-pq[f(c)-f(d)]2＜0

由零值定理可知，至少?一個 ξ∈(c ,d)?(a,b)，使得F(ξ)=0，即 pf (c)+qf(d)=(p +q)f(ξ)。

例 4 設函數f( x)在區間[0,1]上連續，在區間(0,1)內可導，且 f (0)=1， f (1) = 0，證明存在一點 ξ∈ (0,1)使得f(ξ)+ξf'(ξ)=0。

證明 構造輔助函數 F(x )=xf(x)

由已知條件知F(x)在[0,1]上連續，在(0,1)內可導，且有F(0)=F (1)=0，即F(x)在區間[0,1]上滿足羅爾定理的條件，從而在區間(0,1)至少存在一點ξ，使得 F'(ξ)=0，即

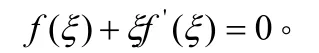
思路總結：先構造輔助函數F(x)，根據已知條件驗證F (x)滿足的條件，然后再根據零值定理和羅爾定理得證。問題的關鍵在于構造恰當的輔助函數，而輔助函數構造的依據就是已經掌握的熟悉的有關定理。

四、輔助函數在討論方程根中的應用

論證方程根的題目，主要有兩類，一類是結合閉區間上連續函數的零點定理去思考，另一類是在已知函數的基礎上論證導函數方程根的情況，此時就要考慮羅爾定理了。

例5 設 a0,a1, …, an為滿足

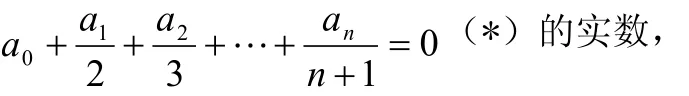
證明：方程 a0+a1x+a2x2+…+anxn=0在(0,1)內至少有一個實根。

在x=1處的函數值F(1)恰好是式子（*），因此該命題可利用羅爾定理來證。

思路總結：（1）只知f(x)在[a,b]或(a,b)上連續，而沒有說明f(x)是否可導，則一般用閉區間上連續函數的零值定理證明；

（2）作出f(x)的一個原函數F(x)，證明F(x)滿足羅爾定理條件，從而得出f(x)的零點的證明。

例6 試討論方程 xe-x=a(a ＞0)的實根。

解 構造輔助函數 F(x)=xe-x-a，則方程xe-x=a的實根個數相當于F(x)的零點個數。為此研究F(x)的單調性及極值（或最值）。令 F′(x)=(1-x)e-x=0?x=1，列表：

x （－∞,1） 1 （1,＋∞）F ＋↑'(x)) F(x) (e-1-a極大值－↓

∵ x=1是F(x)唯一的駐點， F (1)= e-1-a為(-∞,+∞ )上的極大值，因此也是最大值，以下就是F (1)= e-1-a與x軸的相對位置討論F(x)的零點。

10若 F(1 )=e-1-a＜0，即(1, e-1-a)位于x軸的下方，由表單調性所示，F(x)與x軸不會有交點，因此F(x)沒有零點。

20若 F(1 )=e-1-a=0，即 (1,e-1-a)位于x軸上，由表所示，F(x)與x軸除 (1, e-1-a)點外再不會相交，因此F(x)只有唯一的零點。

30若 F(1)=e-1- a＞0，即 (1,e-1-a)位于x軸的上方 ， 由 表 可 知 F(x)在 (-∞,1)內， 且，可知F(x)在(-∞,1)內有且僅有唯一的零點；而F(x)在(1,+∞)內"↓"，且，可知F(x)在(1,+∞)內也有且僅有唯一的零點。總之在這種情況下F(x)在 (-∞, +∞ )內有且僅有二個零點。

綜上所述，當 a ＞e-1時，方程沒有實根； a =e-1時,方程有唯一實根；當 a ＜e-1時，方程有兩個實根。

五、總結

本文主要介紹了輔助函數法在一些數學問題中求解中的巧妙應用，從而體現了輔助函數法的重要性。分別從求極限，證明不等式，證明等式及求解方程根等幾個方面舉例說明輔助函數法的巧妙之處，然而構造輔助函數的內涵十分豐富，沒有固定的模式和方法，是一種創造性的思維活動，一般無章可循，它要求既要有深厚堅實的基礎知識背景，又要有豐富的想象力和敏銳的洞察力。其中心思路是針對問題的具體特點而采用相應的構造方法，從而使論證過程簡潔明了。構造過程充分體現出了數學的發現、類比、逆向思維及歸納、猜想、分析與化歸等思想。使用輔助函數法既能熟練掌握有關定理，提高解題能力，又能開闊思路，鍛煉思維，從而提高數學素質，培養數學能力。

[1] 翟連林，姚正安. 數學分析方法論[M]. 北京：北京農業大學出版社，1992.

[2] 趙刊，吳開祿. 輔助函數在解不等式中的應用[J]. 成都教育學院學報，2000.

[3] 陳文登，黃先開. 考研數學復習指南[M]. 北京：世界圖書出版公司，2008.

[4] 李長青，杜素梅. 輔助函數在證明題中的應用[J]. 勝利油田職工大學學報，2002.

The application of auxiliary function method in some math problem

WANG Li-xia

Auxiliary function is an important thinking method in dealing with math problem. In the course of solving advanced mathematics, we are not always direct to the question itself but base on problems and the known factors to construct a proper auxiliary function to solve the problems indirectly.

auxiliary function method; limitation; zero theorem; Rolle theorem

G42

A

1008-7427（2010）07-0148-02

2010-04-21