蟻群PID神經元網絡在電廠球磨機控制中的應用

沈繼忱，彭猛，宋剛

(東北電力大學自動化工程學院，吉林吉林132012)

0 引言

鋼球磨制粉系統是一典型的具有非線性、大滯后系統，各控制量和被控制量之間存在著相當嚴重的耦合關系。以往的控制系統采用3套相互獨立的PID控制回路，將它們之間的相互關系強行割裂，造成顧此失彼，各調節量之間難以優化匹配，以致制粉系統在低負荷下運行，耗電量很大［1-2］。對此，為了解決這些問題，本文提出了基于蟻群算法的PID神經元網絡控制系統。

1 球磨機制粉系統數學模型

球磨機制粉系統輸入變量分別是給煤量、熱風量和再循環風量，輸出變量分別是球磨機出口溫度、球磨機入口負壓和球磨機負荷，根據300 MW機組配備的球磨機的階躍擾動曲線，取得球磨機制粉

系統的對象特性傳遞函數矩陣為:

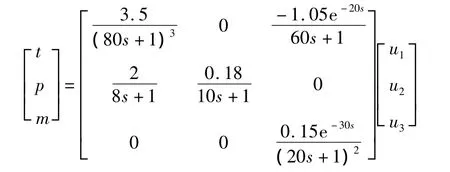
式中，t代表球磨機出口溫度;p代表球磨機入口負壓;m代表球磨機的負荷;u1、u2、u3分別代表熱風門開度、再循環風門開度及給煤量，%。

2 基于蟻群算法的PID神經元網絡控制系統

2.1 控制系統結構

PID神經元網絡控制器是融入PID控制規律的多層前向神經網絡控制器。它融合了常規PID控制器的優點，又具有神經網絡的學習記憶功能和逼近任意函數的能力;并且具有在線學習的功能，隱含層分別定義了比例元、積分元、微分元;通過調整網絡中比例元、積分元和微分元作用的強弱，使被控系統具有較好的靜動態特性，能夠很好地實現系統的控制［3］。根據上述球磨機制粉系統的數學模型，建立了PID神經元網絡球磨機制粉控制系統結構，如圖1所示。

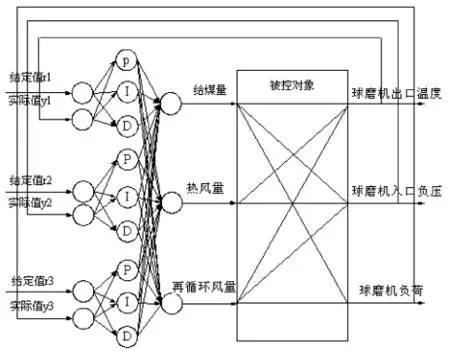
圖1 PID神經元網絡控制系統結構圖

2.2 控制系統的算法

蟻群算法(Ant Colony Algorithm)是一種新型的隨機搜索仿生類算法，1991年由意大利學者M. Dorigo［4］等人首先提出的。他們通過對螞蟻覓食行為的研究，發現螞蟻在其來往路徑上留下一種稱為信息素(Pheromone)的揮發性化學物質，整個蟻群的通信和協調就是通過信息素完成的，從而可以使多個路徑上的螞蟻經過相互協作都逐漸聚集到最短的那條路徑上［5］。

PID神經元網絡和大多數神經網絡一樣采用BP學習算法，由于BP學習算法采用的是局部區域沿梯度下降算法，通常收斂的時間很長，而且不可避免地會陷入局部極值。而蟻群算法適合全局優化搜索，容易得到全局最優解。所以，蟻群算法和PID神經元網絡結合起來組建系統，可兼有PID神經元網絡的廣泛映射能力和蟻群算法的快速、全局收斂以及啟發式學習等特點，在某種程度上避免了PID神經元網絡收斂速度慢，易于陷入局部極小點的問題，提高了控制系統的自學習能力。

基于蟻群算法的PID神經元網絡控制系統的基本思想為:首先利用蟻群算法的全局尋優能力找到一組較優的初始權值組合，再利用BP算法進一步“細調”權值，找到真正的全局最優點。假定網絡中需要優化的權值和閾值總數為s個，先將這些參數依次排序，記為p1、p2、pS，將每個參數設置一個集合Ipi，集合內為N個隨機非零值，設定合適數量的螞蟻，每只螞蟻從第一個集合出發依次走到最后一個集合，在每個集合中依據各元素的信息素的值，按照概率公式選擇一個元素，同時調節所選相應元素的信息素的值，當螞蟻走完s個集合，也就是選擇了一組網絡權值。經過螞蟻的不斷迭代，最終找到最優解。

蟻群算法訓練 PID神經元網絡的實現步驟如下:

a.參數初始化。循環次數NC=0，定義最大循環次數NCmax，將M只螞蟻都置于蟻巢，令集合Ipi(1≤i≤s)內的每一個元素信息量τj(Ip)(t)=C，(1≤j≤N(C為常數)，初始時刻△τij(0)=0。

b.這個步驟重復s次，直到螞蟻走過所有集合。

令s=0

Set s=s+1

For k=1 to M do

每只螞蟻從第一個集合出發依次在每個集合中按照概率式選擇一個元素，對任一只螞蟻k(k= 1，2，…，M)，在集合j中根據下式選擇第j個元素。

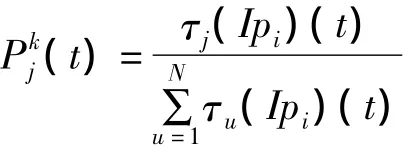
c.當螞蟻走完s個集合，該過程經歷了s個時間單位，對所選元素的信息素按下式做相應調整。τj(Ipi)(t+s)=ρτj(Ipi)(t)+Δτj(Ipi)，其中ρ為信息素軌跡的殘留因子。

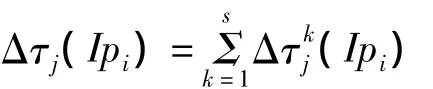
式中，Q是常數，表示完成一次循環后螞蟻所釋放的信息素總量;ek為螞蟻k在本次循環中選擇的元素作為神經網絡的權值時得出的實際輸出與期望輸出之間的誤差。記錄最小誤差對應的權值。

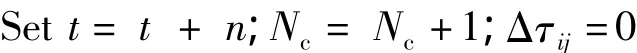
d.If Nc＜NcmaxAND所有的螞蟻沒有選擇同一組權值

Then轉到(2)

否則，輸出最好權值，算法結束。

3 仿真結果

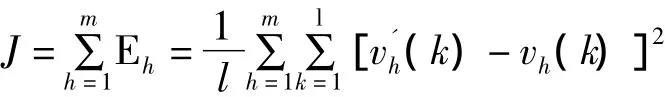
應用蟻群算法找到一組PID神經元網絡的初始權值，蟻群優化的目標是使PID神經元網絡控制系統輸出誤差平方均值為J最小。數目s=45，通常螞蟻數量，其中n為問題的規模，此處n=45，所以螞蟻數量M在7～22之間取值，ρ值的選取通常在0.5～0.7之間算法的性能較為穩定，需要根據仿真實驗的結果適當調整參數大小。通過大量仿真實驗結果分析，信息素殘留系數ρ=0.7，螞蟻數量M=13時蟻群優化PID神經元網絡權值初值效果最好。ρ=0.7，M=13時的優化曲線如圖2所示。

式中，變量個數m=3，采樣點數l=500。

蟻群算法中最大迭代次數 NCmax=50，集合內的隨機數個數N=30，信息素強度Q=10，由于PID神經元網絡采用三輸入、三輸出的形式，所以權值

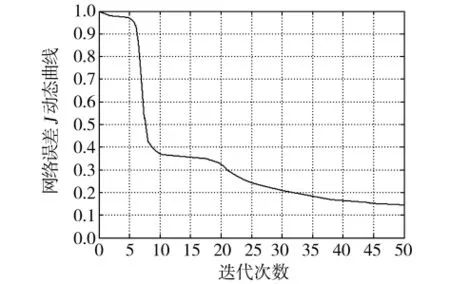
圖2 ρ=0.7，M=13時的優化曲線

為檢驗系統的性能，將經蟻群算法優化得到的PID神經元網絡權值帶入到網絡中，在t=0時刻采用單位階躍輸入對PID神經元網絡進行訓練，系統的響應情況如圖3、圖4、圖5所示。

由以上仿真結果可以看出，因為控制器的初值由蟻群算法訓練，減少了在線調整的計算量和調整時間。蟻群PID神經元網絡有良好的控制品質，優于PID神經元網絡控制算法。

4 結論

應用基于蟻群算法的PID神經元網絡控制器對球磨機制粉系統進行控制仿真，采用蟻群算法優化PID神經元網絡的初始權值，在一定程度上避免了PID神經元網絡收斂速度慢，易于陷入局部極小點的缺陷，實現了球磨機制粉系統的控制效果。

圖3 單位階躍擾動下出口溫度的響應曲線

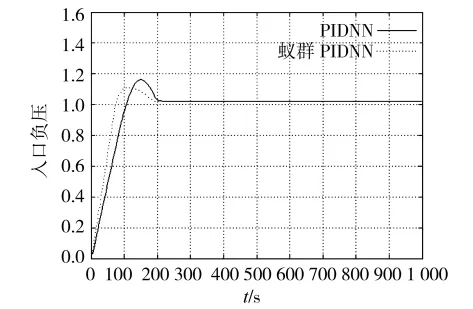
圖4 單位階躍擾動下入口負壓的響應曲線

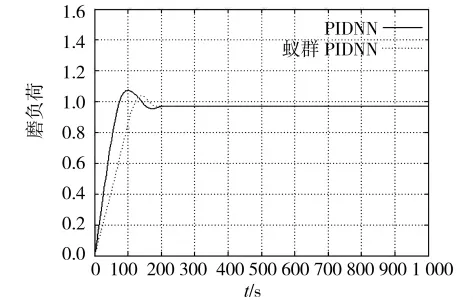
圖5 單位階躍擾動下磨負荷的響應曲線

［1］ 劉全偉，周洪.鋼球磨煤機的模糊神經元解耦控制方法［J］.華北電力技術，2001，7(1):34-36.

［2］ 張驍博，楊建國，趙虹.鋼球磨煤機制粉系統運行優化的試驗研究［J］.動力工程學報，2010，30(2):133-137.

［3］ 舒懷林，PID神經元網絡及其控制系統［M］.北京:國防工業出版社，2006:21-38.

［4］ M Dorigo.Optimization，Learning and Natural Algorithms［D］. Ph.D.Thesis.Department of Electronics，Politecnico Milano，Italy，1992.

［5］ 段海濱.蟻群算法原理及其應用［M］.北京:科學出版社，2005:24-27.