中國人力資本及其分布同經濟增長的關系研究

宋家樂，李秀敏

(東北師范大學 經濟學院，吉林 長春 130117)

一、引言

上世紀80-90年代，以Lucas、Romer為代表的新增長理論把經濟增長主要歸因于人力資本的有效積累。但是，許多實證研究卻得出了相反的結論，即人力資本積累對經濟增長起負向作用，或者影響不顯著［1-5］。對于此，最常見的解釋是人力資本的計算忽略了教育質量問題，從而不能準確評價人力資本對經濟增長的作用;另一個原因是在經濟增長因素中僅考慮人力資本總體水平是不夠的，人力資本分布在經濟發展過程中的作用也是非常重要的。此外，一個國家的政策環境也會影響教育對經濟增長的作用，開放的貿易和投資政策可減少價格扭曲，提高教育回報率，并加強教育對經濟增長的促進作用［6］。

由于缺乏有效數據，關于人力資本分布同經濟增長關系的實證研究并不多，但是研究結論卻明顯不同。大部分實證研究認為，人力資本分布不平衡與經濟增長之間為負相關關系［7-17］，但聶江(2006)認為，這種負相關關系不具有長期穩定性［18］;而 Park(2006)的檢驗結果表明，人力資本分布不平衡同經濟增長之間則為正相關關系［19］;Digdowiseiso(2009)的研究結論卻是人力資本分布不平衡對經濟增長的影響不顯著［20］;張錦華等(2005)的研究表明，人力資本不平等對地區經濟增長的影響會經歷一個先揚后抑的過程［21］;Lopez等(1998)、王家贈(2002)［22］的研究卻表明人力資本分布不平衡與經濟增長的關系在不同的國家或地區有不同的表現:在有些國家或地區是負相關關系，在有些國家或地區則是正相關關系，而在有些國家或地區卻不相關。

產生上述分歧的原因主要有:一是所用數據不同，既有跨國的截面數據和面板數據，也有中國的時間序列數據，還有中國各省、自治區與直轄市的面板數據。跨國的數據多為5年間隔，中國時間序列數據的時間長度較短。二是模型設定方面差異較大，大部分研究都是在科布-道格拉斯生產函數的基礎上加入人力資本和人力資本分布變量，或者以人力資本和人力資本分布變量替代勞動力變量，僅有Lopez等(1998)和Park(2006)在數理推導的基礎上建立實證分析模型;也有直接對人力資本不平等與經濟增長之間的關系進行協整檢驗和因果關系檢驗;大部分研究采用線性模型進行估計，也有研究采用線性模型和非線性模型同時估計。Thomas等(2001)認為總量生產函數可能是非線性的，而且，由于教育基尼系數同平均受教育年限之間存在負相關關系，將二者同時作為解釋變量放入同一線性回歸模型會存在多重共線性的問題，從而造成偽回歸［23］。三是指標選取方面也明顯不同，反映經濟增長的指標有國內生產總值(GDP)、人均GDP、勞動生產率和全要素生產率等，反映人力資本分布的指標有教育基尼系數、教育方差、教育方差系數及教育標準差等。四是大部分研究認為人力資本形成函數是線性的，因而忽略了人力資本庫茲涅茨曲線存在的可能性。

與已有對中國的相關實證研究不同，本文采用Park(2006)的模型檢驗中國1952-2009年人力資本水平和人力資本分布同勞動生產率的關系，該模型考慮人力資本形成函數的非線性特征，經過數理推導將人力資本不平等指標納入回歸模型，從而可以檢驗庫茲涅茨曲線的存在性。本文另外一個明顯特征是采用中國58年的連續數據對該模型進行實證檢驗，得到了與大多數實證研究不同的結論，即中國人力資本水平和不平等對經濟增長均具有正向作用;而且，這一結論說明，中國的人力資本變化符合庫茲涅茨曲線規律，且處于庫茲涅茨曲線的左側。為了加快經濟增長，中國應全面發展各層次教育，促進人力資本水平和不平等程度的提高。

本文余下部分的結構安排如下:第二部分介紹實證檢驗的基本模型;第三部分為相關數據的說明與處理;第四部分為實證檢驗;最后為本文的結論與政策建議。

二、基本模型

本文采用Park(2006)的模型對中國人力資本水平和人力資本分布同經濟增長的關系進行實證檢驗。該模型按如下思路建立:

考慮一個產出由兩種生產要素生產的經濟，生產技術符合規模報酬不變的科布-道格拉斯生產函數，即:

式(1)中，Yt、Kt和 Lt分別代表第 t期的 GDP、資本和勞動力，At代表由效率提高與知識環境決定的技術進步率，β為資本產出彈性，且有0＜β＜1。

將式(1)的兩邊同時除以Lt，得到生產函數的緊湊形式:

式(2)中，yt、kt分別代表勞動生產率(Yt/Lt)和勞均資本(Kt/Lt)。對式(2)的等號兩端同時取對數，并對時間t求導，將其轉化為增長率形式，有:

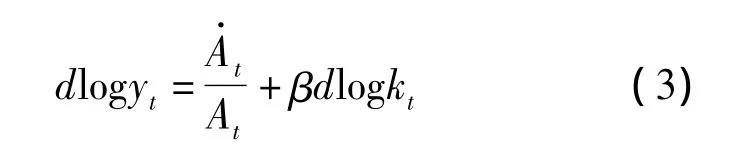
式(3)中，dlogyt表示 yt的增長率，表示技術進步的變化率，表示技術進步率;dlogkt表示kt的增長率。

根據內生經濟增長模型，人力資本積累能夠促進技術進步。假設每單位勞動的人力資本影響技術進步率，并考慮追趕效應，則技術進步率由下式表示:

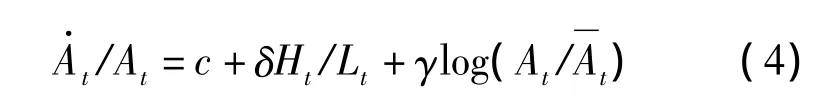
式(4)中，c為不變的技術進步率，Ht為經濟中的人力資本存量表示擁有最先進技術國家的技術水平，δ、γ分別表示生產率增長的人力資本效應和追趕效應。

給定經濟中第t期代表性個體的人力資本，定義總量人力資本Ht是經濟中所有個體人力資本的總和，即:

n代表經濟中的人口數。假設每個人在調整有效單位時其人力資本是完全可替代的，每個人的人力資本是其接受的教育(sit)和因工作經歷而獲得的技能(xit)的函數，可表示為:

由于很難獲得關于工作經歷的數據，因此通常假定每個人的人力資本只由其所接受的教育(sit)決定。而且，大多數研究都假設g為線性函數，即對于所有教育水平每增加一年的教育會增加固定數量的人力資本，也就是說，每增加一年教育投資的機會成本是常數，因此教育回報率也為常數。但是，如果不同的教育水平所獲得的知識類型不同，不同水平教育的回報率也許是非線性的。給定相同數量的教育投資，或者說人口的平均受教育年限相同，如果教育回報函數是非線性的，總量人力資本的構成則至關重要。

為了考察人力資本的生產技術是否是非線性的，對函數g在第t期的平均受教育年限處進行泰勒展開，并將其近似為:

整理式(9)，并用工人受教育年限的平均值(μt)和方差來表示勞均人力資本，式(9)可

式(12)表明，勞動生產率增長率由工人的平均受教育年限和反映人力資本分布不平衡的教育方差決定。g的函數形式將經濟增長同人力資本分布聯系起來。無論函數g是凸函數還是凹函數，都決定了人力資本分布的重要性。如果g″與0沒有區別，那么，僅考慮平均受教育年限對經濟增長的影響是恰當的。然而，如果g″顯著不為0，則人力資本分布會影響經濟增長。如果g″為正，說明教育回報率是遞增的，人力資本分布處于庫茲涅茨曲線的左側，在平均受教育年限相同的情況下，教育分布越不平衡，經濟增長越快;反之，如果g″為負，說明教育回報率是遞減的，人力資本分布處于庫茲涅茨曲線的右側，在平均受教育年限相同的情況下，教育分布越平衡，經濟增長越快。

式(12)的政策含義十分明顯，在教育資源有限的情況下，為了促進經濟增長，政府是應該支持精英教育，培養少數精英，保持人力資本的相對平衡，還是應該支持所有層次的教育，即全民教育，加速人力資本分布的不平衡。

三、相關數據的說明與處理

對式(12)進行檢驗的關鍵是估算中國的物質資本、人力資本和人力資本分布及同技術最先進國家的技術差距()的數據。計算和檢驗所用數據主要來源于《新中國五十五年統計資料匯編》、《新中國六十年統計資料匯編》、《中國國內生產總值核算歷史資料1952-2004》、2006-2010年的《中國統計年鑒》及美國經濟分析局(Bureau of Economic Analysis)和人口普查局(Census Bureau)的統計數據庫。

(一)物質資本的計算

本文用固定資本存量表示物質資本，并采用永續盤存法計算中國1952-2009年各年的固定資本存量Kt，計算公式為:

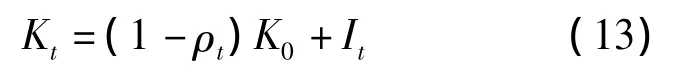
其中，K0為基期的固定資本存量，ρt為第 t年的折舊率，It為第t年新增的固定資本，t=1952，…，2009。根據式(13)進行計算的關鍵是確定基期(1952年)的固定資本存量K0、每年的折舊率ρt和每年新增的固定資本It。

借鑒已有研究成果［24-27］，確定1952年的固定資本存量為800億元;按固定折舊率5%計算;每年的新增固定資本用每年的固定資本形成額表示，并換算為1952年價格。1952-2004年的固定資本形成額直接依據1952年的固定資本形成額和固定資本形成總額發展速度換算，并求出各年以1952年為100的固定資本形成價格平減指數，以該價格平減指數為基礎，根據2005-2009年以上年為100的固定資產投資價格指數(將其近似為固定資本形成價格平減指數)計算出2004-2009年以1952年為100的固定資本形成價格平減指數，再將各年當年價的固定資本形成額換算成1952年價格。計算結果見附表1。

(二)人力資本和人力資本分布的計算

本文以15歲及以上人口的平均受教育年限和教育方差表示工人受教育年限的平均值(μt)和人力資本分布()，其計算公式為:

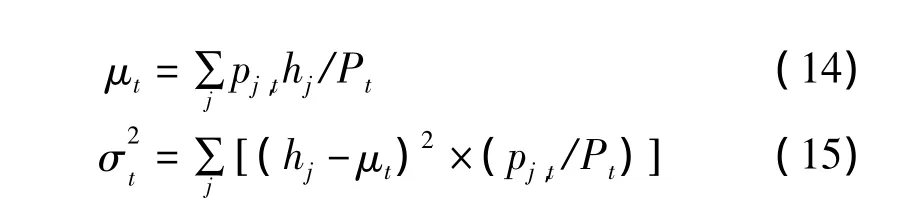
式(14)和(15)中，j為受教育程度，j=0，1，2，3，4，依次表示小學以下、小學、初中、高中和大學教育程度;pj，t為15歲及以上人口中第j層次受教育程度的人口數，hj為第j層次受教育程度的受教育年限，小學以下、小學、初中、高中及大學教育程度的受教育年限依次為2年、6年、9年、12年與16年;Pt為15歲及以上人口總數。

對于各層次受教育程度的人口數，本文借鑒Barro 和 Lee(2000)［28］及 Wang 與 Yao(2003)［29］的方法，按如下公式計算:

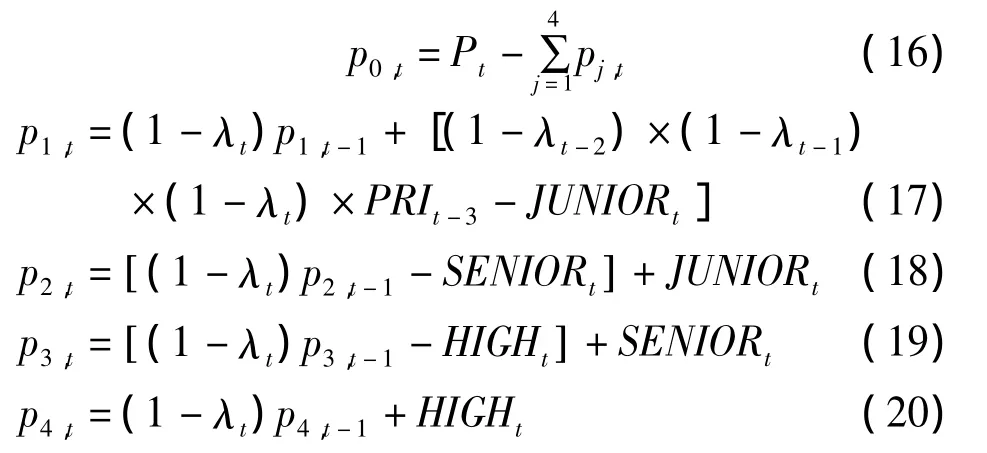
式(15)-(19)中，PRIt、JUNIORt、SENIORt和HIGHt分別表示第t年小學、初中、高中及大學的畢業生數;λt表示第t年總人口的死亡率。

由于缺乏1952年各層次受教育程度人口數，本文以1964年第二次人口普查數據為基礎推算1952-2009年各年各層次受教育程度人口數①具體推算方法參見宋家樂和李秀敏(2010)［30］。

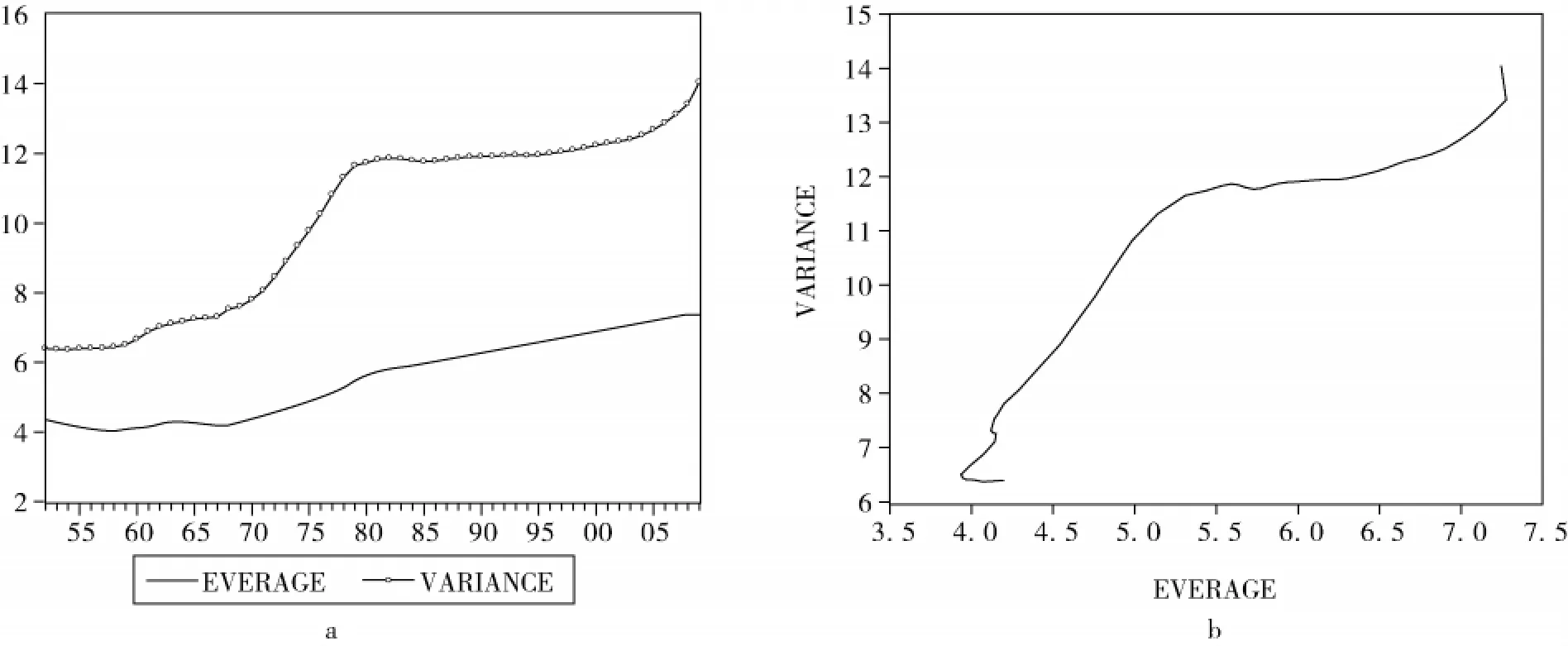
圖1 1952年以來中國人力資本與人力資本分布的關系

再根據式(14)和(15)計算1952-2009年15歲及以上人口的平均受教育年限及教育方差，計算結果見附表1，1952-2009年的平均受教育年限和教育方差及其相互關系見圖1。

從圖1中的a圖可以看出，1952年以來中國的人力資本水平不斷提高，人力資本分布的不平衡程度經歷了1952-1979年的迅速擴大、1979-1995年的相對穩定及1995年以來的再度擴大的變化過程。圖1中的b圖表明，隨著人力資本水平的提高，人力資本分布不平衡的程度不斷擴大，目前尚處于庫茲涅茨曲線的左側。

(三)同技術最先進國家的技術差距()的計算

本文借鑒Park(2006)的方法，選擇美國為技術最先進的國家，并用1952-2009年各年中國同美國人均GDP(當年價)的比值表示中國同技術最先進國家的技術差距之所以選擇當年價格的人均GDP計算，主要是因為人們往往根據現價衡量同美國的差距。另外，中國的人均GDP按照各年人民幣對美元的匯率折算成為美元。的計算結果見附表1。

四、實證檢驗與分析

為了方便檢驗，本文參考Park(2006)的方法將式(12)簡化為:

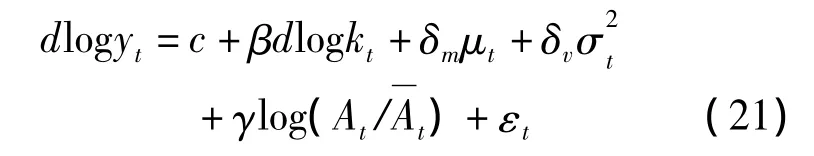
其中，δm、δv分別表示人力資本和人力資本分布的回歸參數，εt為殘差項，其分布滿足i.i.d.(o，σ2ε)。技術差距變量采用滯后一期的數值，以避免其同殘差項相關。

對初次回歸結果進行懷特異方差性檢驗得知，模型存在異方差性，因此采用加權最小二乘法進行回歸，權重為殘差絕對值的倒數，回歸結果見表1。

從表1可以看出，加權的回歸結果明顯好于不加權的回歸結果。因此，采用加權回歸分析法是恰當的。另外，回歸方程擬合優度較好，且通過了t檢驗、F檢驗、自相關檢驗和White檢驗。回歸結果表明，勞均資本的增長率、人力資本和人力資本不平等對中國勞動生產率提高的影響顯著為正。其中，勞均資本增長率的影響最大，勞均資本每增加1個百分點，勞動生產率約提高0.65個百分點;其次為人力資本，人力資本每提高1年，勞動生產率將提高0.01個百分點;人力資本分布的影響最小，人力資本分布越不平衡，勞動生產率提高越快，教育方差每擴大一個單位，勞動生產率提高0.003個百分點。追趕效應的影響非常明顯，中美人均GDP比值的對數每降低1個單位，中國勞動生產率約增長0.05個百分點。

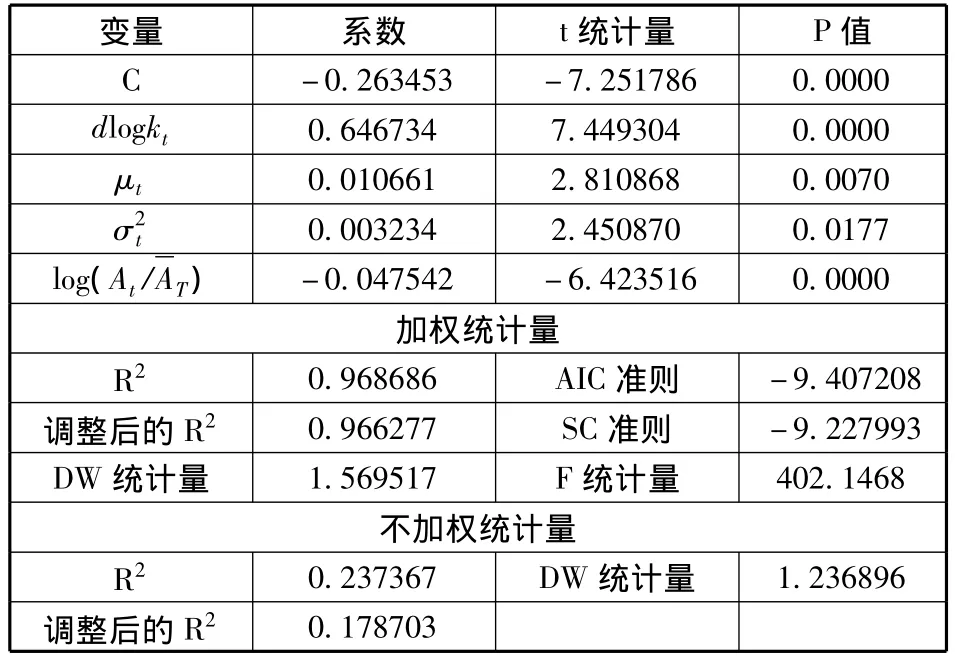
表1 模型回歸結果

五、結論與政策建議

本文采用Park(2006)的回歸模型，運用中國1952-2009年的數據檢驗了人力資本與人力資本分布對勞動生產率的影響。回歸結果表明，在控制追趕效應的前提下，人力資本水平提高能夠促進勞動生產率的提高，這方面與已有的大部分研究結論相同;同時，人力資本分布不平衡對勞動生產率的提高也起促進作用，這同以往的大部分研究結論相反，但卻與Park(2006)的理論與實證結果相一致，并證實了教育回報函數的凸性假設，即每增加一年較高水平的教育所帶來的人力資本的增量是遞增的。此外，本研究還表明，建國以來中國的人力資本水平不斷提高，人力資本分布的不平衡程度不斷擴大，中國尚處于庫茲涅茨曲線的左側，即隨著人力資本水平的提高，人力資本分布的不平衡程度不斷擴大;而且，勞均資本的增加仍是勞動生產率提高的最主要源泉，追趕效應的作用也很明顯。

根據上述結論，本文認為，中國應該轉變增長方式，把人力資本投資作為經濟增長的主要源泉。在當前教育資源有限的情況下，政府應該支持所有層次教育的發展，不僅要繼續普及9年義務教育，還要普及高中階段教育，加快大學階段教育的發展，為廣大青少年提供更多的接受高中和大學階段教育的機會。鼓勵有條件的地區推行高中義務教育，將9年義務教育擴大至12年義務教育，并加大對大學階段教育的公共投資力度。總之，中國目前應該堅持全民教育，繼續增加人力資本積累，雖然會擴大人力資本分布的不平衡，但對經濟增長會具有雙重促進作用，而且，還會提高勞動者的談判能力，這將有助于解決勞資分配失衡的問題。

［1］林毅夫等.中國的經濟發展戰略與地區收入差距［J］. 經濟研究，2003，(3):19-25.

［2］羅伯特·巴羅等.經濟增長［M］.北京:中國社會科學出版社，1999.393-435.

［3］姚先國等.教育、人力資本與地區經濟差異［J］.經濟研究，2008，(5):47-57.

［4］ C.I.Jones.Time Series of Endogenous Growth Models［J］.Quarterly Journal of Economics，1995，110(2):495-525.

［5］L.Pritchett.Where Has All the Education Gone?［R］.Policy Research Working Paper，1996，No.1581.

［6］Lopez R.，etc.Addressing the Education Puzzle:The Distribution of Education and Economic Reforms［R］.World Bank Working Papers，1998，No.2031.

［7］Birdsall N.，etc.Asset Inequality Matters:An Assessment of the World Bank’s Approach to Poverty Reduction［J］.A-merican Economic Review，1997，87(2):32-37.

［8］Castelló A.，etc.Human Capital Inequality and Economic Growth:Some New Evidence［J］.Economic Journal，2002，112(478):187-200.

［9］劉海英等.人力資本“均化”與中國經濟增長質量關系研究［J］.管理世界，2004，(11):15-21.

［10］張長征等.中國教育公平與經濟增長質量關系實證研究:1978-2004［J］. 經濟理論與經濟管理，2005，(12):20-24.

［11］李忠強等.人力資本、人力資本不平等與地區經濟增長:一個實證研究［J］.中國人口科學，2005，(Z):105-110.

［12］李亞玲等.人力資本分布結構與區域經濟差距——一項基于中國各地區人力資本基尼系數的實證研究［J］.管理世界，2006，(12):42-49..

［13］楊俊等.教育不平等、人力資本積累與經濟增長:基于中國的實證研究［J］.數量經濟技術經濟研究，2007，(2):37-45.

［14］李秀敏.人力資本、人力資本結構與區域協調發展——來自中國省級區域的證據［J］.華中師范大學學報(人文社會科學版)，2007，(3):47-56.

［15］李晶瑩等.人力資本不平等對經濟增長的影響研究［J］. 預測，2008，27(4):11-15，45.

［16］魏下海等.人力資本、人力資本結構與區域經濟增長——基于分位數回歸方法的經驗研究［J］.財貿研究，2009，(5):15-24.

［17］湯華然等.人力資本不平等與區域間經濟差異［J］.重慶社會科學，2010，(4):35-40.

［18］聶江.人力資本不平等與經濟發展的協整性及因果分析［J］. 統計與決策，2006，215(6):74-75.

［19］Park Jungsoo.Dispersing of Human Capital and Economic Growth［J］.Journal of Macroeconomics，2006，28(3):520-539.

［20］ Digdowiseiso Kumba.Education Inequality，Economic Growth and Income Inequality Evidence from Indonesia，1996-2005［R］.MPRA Paper，2009，No.1779.

［21］張錦華等.教育不平等、增長非平衡與低發展陷阱——對農村教育和農村經濟協調發展的考察［J］.當代財經，2006，265(12):20-27.

［22］王家贈.教育對中國經濟增長的影響分析［J］.上海經濟研究，2002，(3):10-17.

［23］ Thomas V.，etc.Measuring Education Inequality:Gini Coefficients of Education［R］.World Bank Policy Research Working Paper，2001，No.2525.

［24］賀菊煌.我國資產的估算［J］.數量經濟與技術經濟研究，1992，(8):24-27.

［25］G.C.Chow.Capital Formation and Economic Growth in China［J］.Quarterly Journal of Economics，1993，108(3):809-842.

［26］張軍等.對中國資本存量K的再估計［J］.經濟研究，2003，(7):35-43.

［27］張軍等.中國省際物質資本存量估算:1952-2000［J］. 經濟研究，2004，(10):35-44.

［28］Barro R.J.，etc.International Data on Educational Attainment:Updates and Implications.CID Working Paper，2000，No.42.

［29］ Wang Y.，etc.Sources of China’s Economic Growth 1952-1999:Incorporating Human Capital Accumulation［J］.China Economic Review，2003，14(1):32-52.

［30］宋家樂等.中國經濟增長的源泉:人力資本投資［J］.中央財經大學學報，2010，(12):56-61.

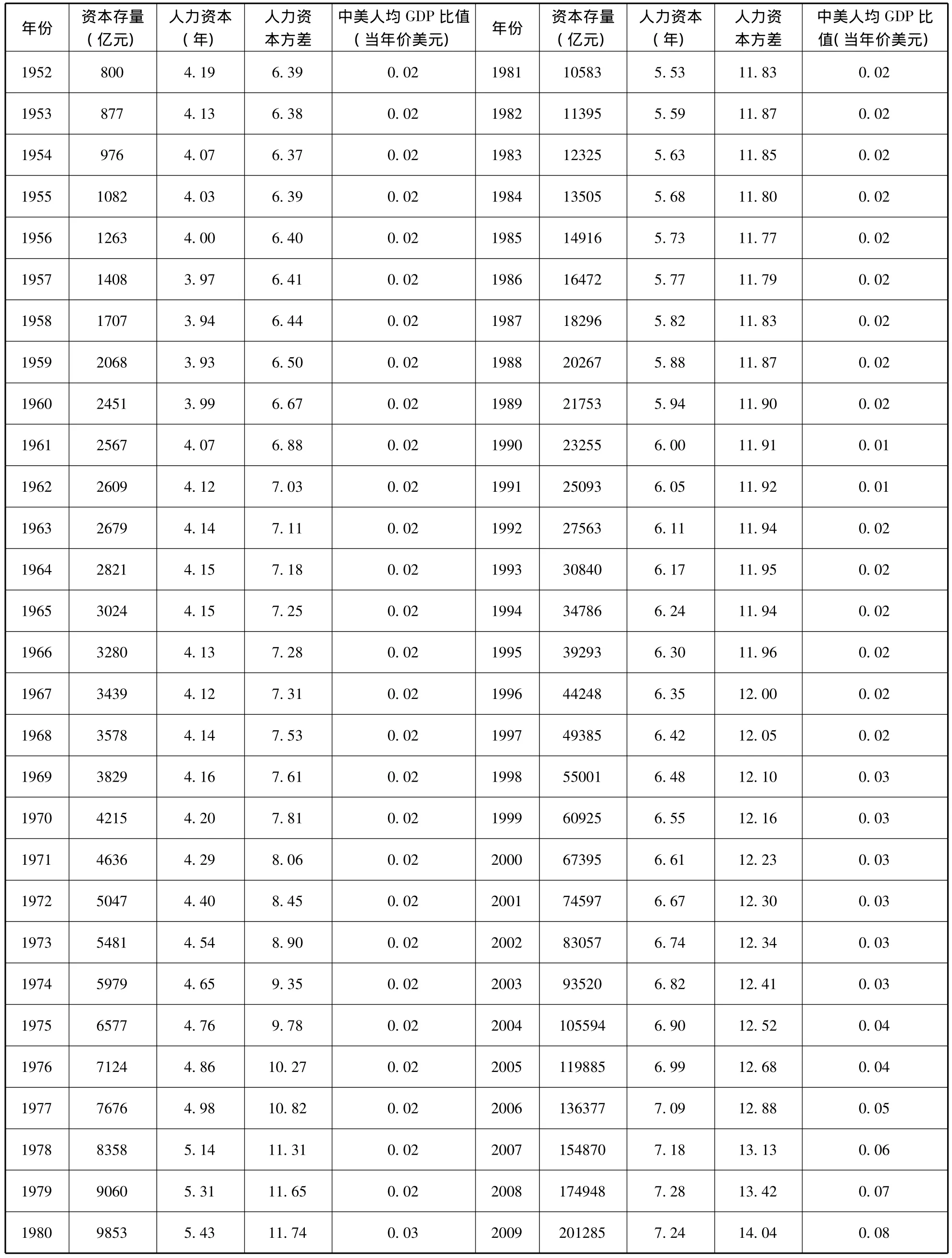
附表1 本文所用的主要數據