沖擊載荷下自增強身管殘余應力變化規律＊

李 強，李鵬輝，趙君官，茹站勇

（1.中北大學動力機械系，山西 太原 030051；2.中國船舶重工集團公司第713研究所，河南 鄭州 450015）

速射武器身管在發射過程中隨著連發數的增加，熱應力逐漸成為影響身管應力的主要因素。雖然自緊殘余應力可以有效抵消部分火藥燃氣壓力，但同時又與熱應力的方向相同，使身管內的壓縮切向應力提高，使身管產生塑性變形，從而使局部區域的應力重分布。姚建軍等［1］、佘建生［2］采用間接耦合的方法，分析了不考慮屈服時速射武器身管在火藥燃氣壓力和溫度共同作用下的溫度和應力。胡振杰［3］分析了大口徑火炮連發時身管的應力，但由于射速很低，與速射火炮身管應力有很大不同。火藥燃氣壓力和熱應力對身管的作用是瞬態沖擊，因此采用直接耦合的方法和足夠小的計算時間間隔，有利于充分地將這兩者對身管的瞬態動力響應計算出來。本文中，針對速射火炮鍍鉻自緊身管（射速800min－1），考慮火藥燃氣和熱應力作用，使用Ansys有限元分析軟件，建立身管膛壓最高處截面的平面有限元模型，采用直接耦合方法，模擬連發過程中自緊身管的應力和塑性變形，分析殘余應力的變化規律。

1 熱結構耦合基本方程

火炮在發射時，身管承受強烈的熱沖擊和壓力載荷沖擊作用，熱結構耦合問題基本方程包括考慮身管結構變形的熱傳導方程和考慮慣性效應的熱彈性方程。

根據熱力學和傳熱學關系，可導出熱傳導基本方程式［4］

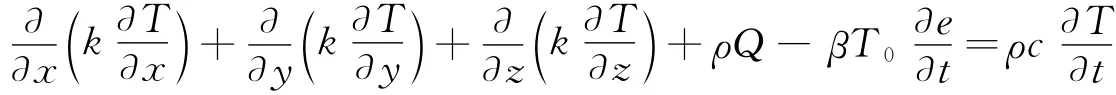
式中：Q為單位時間內吸收的熱量；T0為物體初溫；e＝εx＋εy＋εz，為總應變；β為熱應力系數；k為傳熱系數；c為比熱容；ρ為材料密度。

根據熱彈性理論，由運動方程、幾何方程和物理方程，建立熱彈性理論位移法基本方程式式中：λ和G為拉梅系數。

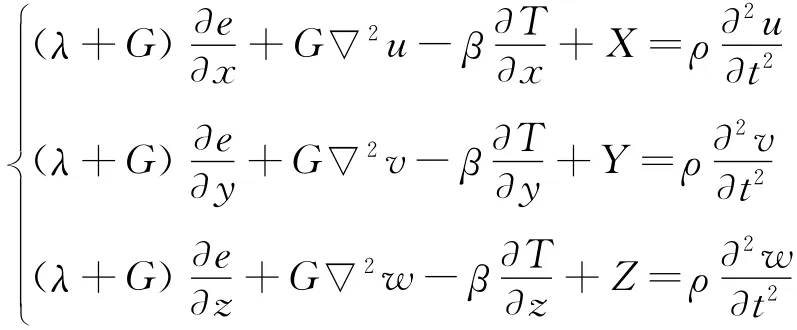
在采用直接耦合法求解熱彈性問題時，必須聯立求解熱傳導方程式和熱彈性基本方程式。

2 直接耦合分析模型及實現方法

2.1 身管有限元模型

身管由炮鋼基體和極薄的鉻層組成。炮鋼物性參數為［5］：密度ρ＝7 833kg／m3，傳熱系數k＝40W／（m2·K），泊松比μ＝0.3，比熱容c＝460.0J／（kg·K），熱膨脹系數α＝1.25×10－5K－1，彈性模量E＝206GPa，屈服應力σs＝1GPa，切線模量ET＝20.6GPa。鍍鉻層是硬脆性材料，假設鉻層未發生塑性變形，物性參數為：密度ρ＝7 190kg／m3，傳熱系數k＝67W／（m2·K），泊松比μ＝0.3，比熱容c＝460.5J／（kg·K），熱膨脹系數α＝6.2×10－6K－1，彈性模量E＝254GPa。鉻層的傳熱系數、彈性模量和熱膨脹系數與炮鋼的差別較大。

以身管最高膛壓截面作為研究對象，并假設身管內外壁光滑無損傷。材料采用雙線性隨動強化模型，不考慮材料性能隨溫度的變化。由于對稱性，選用該截面四分之一模型，鉻層與基體模型通過命令GLUE連接在一起。因內壁溫度載荷的劇烈變化，對身管內壁薄層進行細化。單元選用熱－結構直接耦合平面單元plane 13，取身管應力狀態為平面應力，有限元模型如圖1。

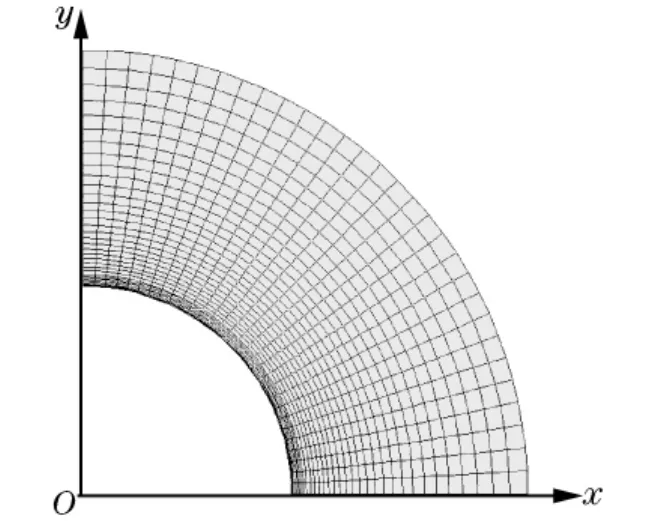
圖1 身管有限元模型Fig.1Finite element model of barrel

2.2 邊界條件的確定

身管邊界條件有內壁火藥燃氣壓力（見圖2）、內壁環境溫度、內壁對流放熱系數和外壁對流放熱系數、外壁環境溫度，為簡化取外壁環境溫度為293K。通過APDL語言［6］將邊界條件的計算寫入到ANSYS命令流中計算，實現多次連發模擬。

內彈道時期火藥燃氣的溫度

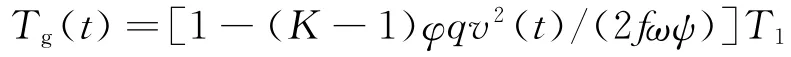
式中：v（t）為彈丸運動速度；K為絕熱指數；ω為裝藥量；f為火藥力；φ為虛擬系數；q為彈丸質量；ψ為火藥燃去部分百分比；T1為火藥爆溫［2］。后效期溫度［7］

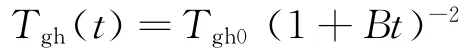
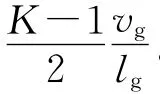
火藥燃氣的放熱系數

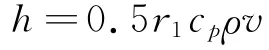
式中：cp為火藥燃氣的定壓比熱容，cp＝1.799kJ／（kg·K）；ρ、v為火藥燃氣的密度和速度；r1為摩擦因數，r1＝（A＋4lgd）－2，d的單位為cm，A為經驗常數，A＝13.2［8－9］。內壁對流放熱系數如圖3所示。

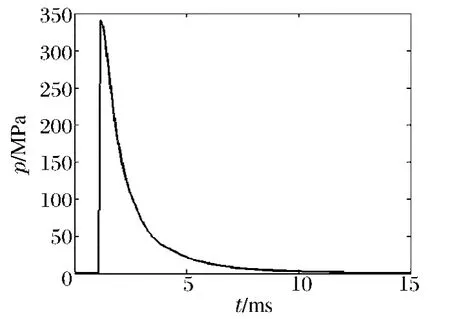
圖2 火藥燃氣壓力時間曲線Fig.2Pressure－time curve of powder gas

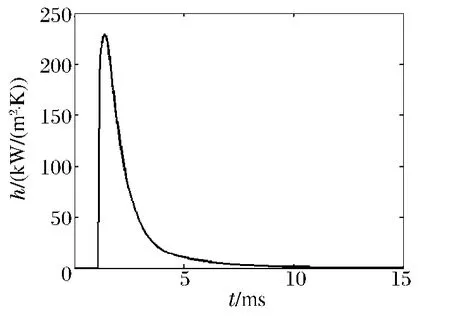
圖3 火藥燃氣放熱系數曲線Fig.3Convection coefficient of powder gas

射擊間隔，身管內空氣對流放熱系數

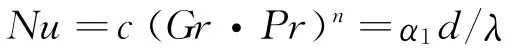
式中：格拉曉夫相似準則Gr＝gβΔTd3／ν2；取常數c＝0.54，n＝0.25；λ、ν為空氣的熱導率、運動粘度；α1為空氣的對流換熱系數；β為空氣的容積膨脹系數，β＝1／（T＋273）；T為定性溫度，T＝（T0＋Tb）／2；ΔT為身管冷卻開始時內表面與環境的溫度差。

2.3 自緊殘余應力模擬方法

生產中自緊殘余應力產生的過程，在模擬中通過加卸載、鍍鉻3個過程來實現。第1步，采用生死單元技術，殺死內壁鉻層單元，在基體內表面上施加自緊壓力，計算；第2步，在基體內表面施加大小為零的壓力，計算；第3步，激活鉻層單元。這其中需要在分析前關閉時間效應積分，這樣身管內就產生了殘余應力。

3 分析討論

分析過程是：先分析身管30%自緊后產生的殘余應力；然后分析自緊身管在50連發過程中身管的塑性變形，以及冷卻后殘余應力的變化；最后分析再連發10發過程中的塑性變形，和冷卻后的殘余應力的變化。

3.1 連發過程中身管溫度變化

圖4是連發過程中不同半徑處的溫度變化曲線，l為距內壁距離。可以看出，內壁瞬時溫度很高，在800～1 200K，而且沿半徑方向溫度差距較大。說明熱量的傳播速度相對于射速來說比較小，徑向較大的溫度差使得內壁存在較大的熱應力。

3.2 連發過程中塑性變形變化

圖5是50連發過程中等效塑性應變的變化。可以看出，身管內壁約1.37mm的薄層發生了較大的塑性應變，而且在約0.61mm內壁薄層塑性應變經歷了先減小后增大的過程，塑性應變趨于穩定。殘余應力發生了重新分布。圖6是冷卻后再連發10發過程，約0.37mm薄層又發生了塑性變形，殘余應力又進行了重新分布。這說明連發過程中，身管在自緊殘余應力、熱應力和火藥燃氣壓力作用下身管發生持續反復的塑性變形。

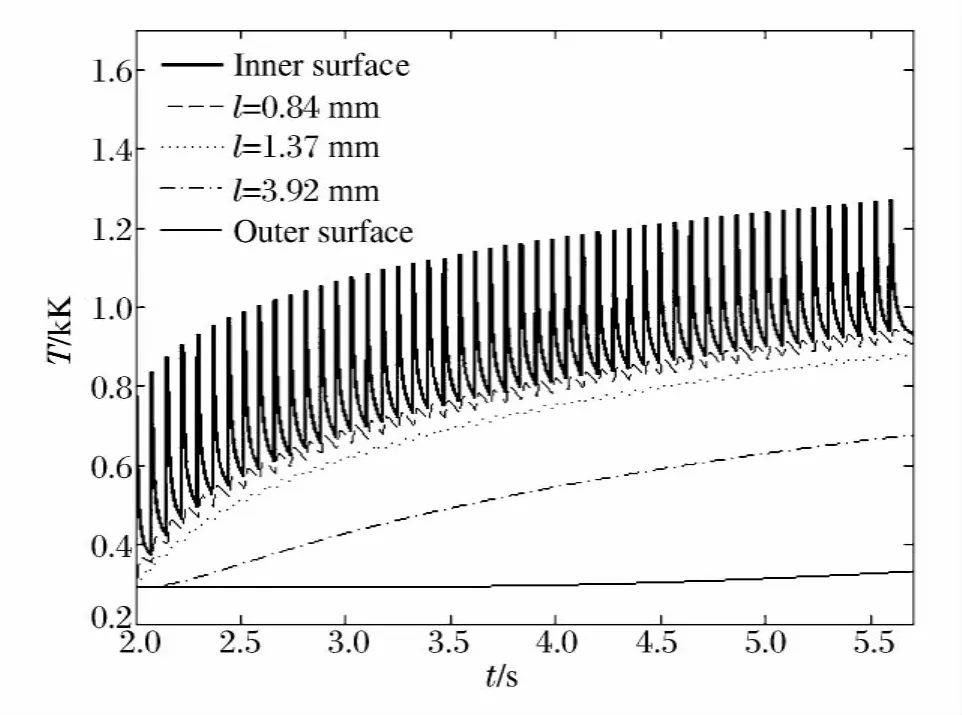
圖4 溫度時間曲線Fig.4The temperature－time curve

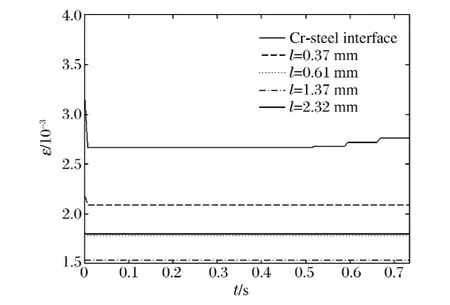
圖6 后續10連發過程中等效塑性應變時間曲線Fig.6The equivalent plastic strain－time curve in the process of 10continuous emission after cooling

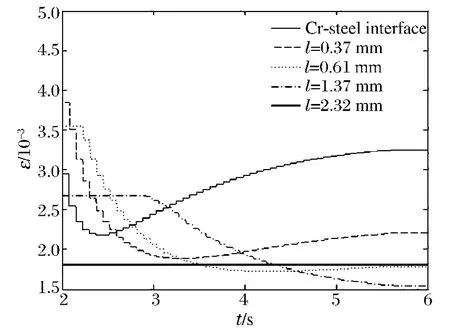
圖5 50連發過程中等效塑性應變時間曲線Fig.5The equivalent plastic strain－time curve in the process of 50continuous emission

3.3 連發過程中身管應力變化

圖7是不同半徑處的應力時間曲線，可以看出內壁薄層（約1.37mm）的最大應力在若干連發后便在材料的屈服強度1GPa附近。而且沿半徑方向應力差距較大。由于熱應力和起始殘余應力的作用，使內壁存在較大的壓縮切向應力，發生壓縮屈服，身管的殘余應力進行了重新分布。

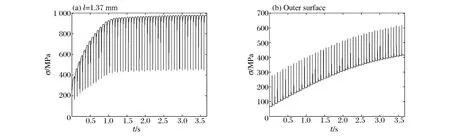
圖7 等效應力時間曲線Fig.7Stress－time curves in the radial orientation

3.4 不同發射狀態塑性應變變化

圖8是不同發射狀態身管塑性應變對比。可以看出，整個過程中塑性變形變化的區域在內壁約2.3mm內。50連發過程中，隨著連發數的增大拉伸切向塑性應變逐漸減小，直至轉變為壓縮塑性應變，壓縮徑向塑性應變逐漸減小，拉伸軸向塑性應變逐漸增大，而且越靠近內壁變化越大。這主要是熱應力逐漸增大的結果。再連發10發后，內壁約0.5mm薄層塑性應變又發生了變化，其中壓縮切線塑性應變減小，壓縮徑向塑性應變增大，拉伸軸向塑性應變減小。

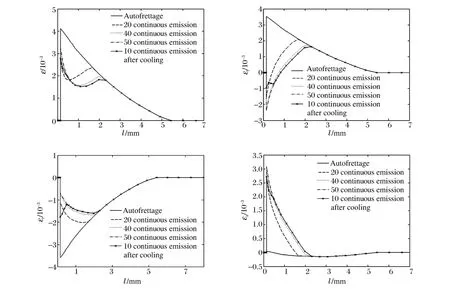
圖8 不同發射狀態等效塑性應變Fig.8Plastic strains under different conditions

3.5 不同發射狀態殘余應力變化

圖9是不同發射狀態的殘余應力對比。可以看出，50連發冷卻后壓縮徑向殘余應力減小，并且內壁局部區域轉變為拉伸徑向殘余應力，在距內壁約2mm身管壓縮切向殘余應力減小，局部區域轉變為拉伸殘余應力，在2mm以外壓縮切向殘余應力增大。冷卻后再連發10發冷卻后，殘余應力變化不大，只是內壁約0.5mm的身管內拉伸切向殘余應力大幅減小。

首先，自緊殘余應力抵消了部分火藥燃氣壓力的作用，不會產生塑性變形，然后，隨著溫度的升高和連發數的增加，熱應力逐漸增大，并與自緊殘余應力疊加，使得這一薄層內的應力很快超出了材料的屈服極限，產生了壓縮切向塑性變形，從而切向殘余應力發生變化。在后續10連發過程中，由于火藥氣體壓力使身管產生拉伸切向應力，它與拉伸切向殘余應力相疊加。因此在第一發時身管內壁薄層的拉伸切向殘余應力最大，已經超出了材料的屈服強度，發生拉伸切向屈服變形，殘余應力又進行了重新分布。在這10連發中，重新分布的殘余應力已經不能再抵消熱應力，身管屈服，如圖8所示，第8發時緊貼交界面基體又發生塑性變形來抵消熱應力。從這個分析可以看出，身管內壁發生了反復的塑性變形。

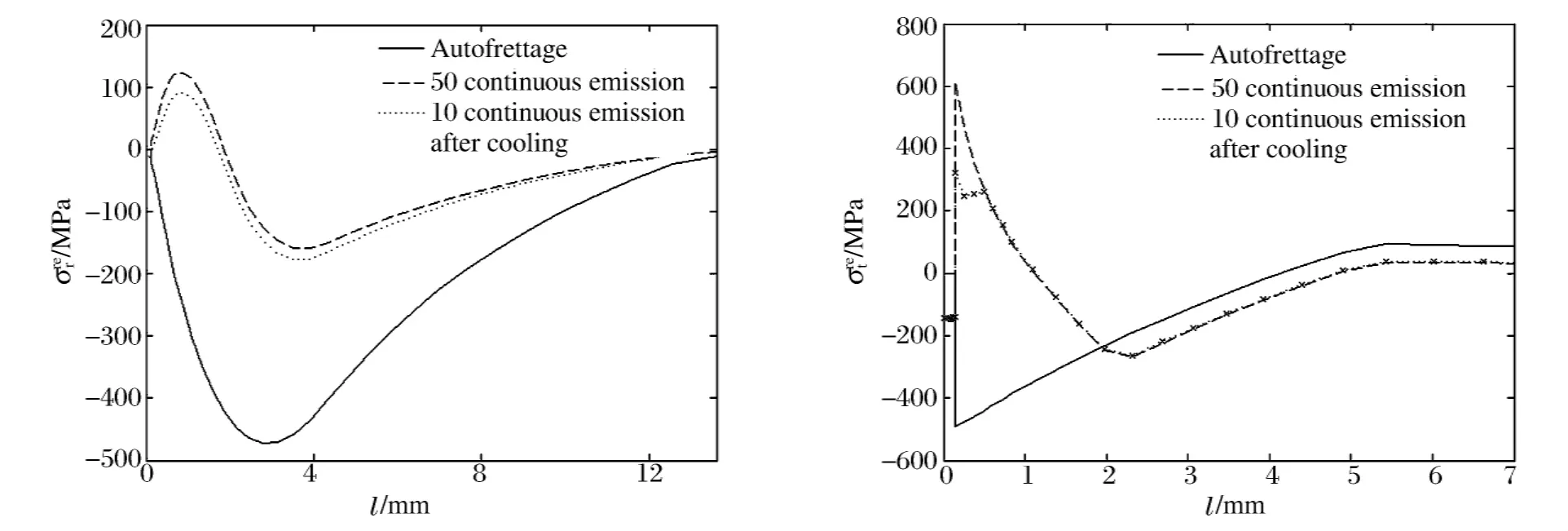
圖9 不同發射狀態殘余應力Fig.9Residual stresses under different conditions

4 結 論

（1）殘余應力變化的原因：逐漸增大的熱應力與初始殘余應力的疊加引發了壓縮的切向塑性應變，在內壁薄層區域產生了與火藥燃氣壓力方向相同的殘余應力，再次發射時與火藥燃氣壓力相疊加，發生反向屈服。可以預測，隨著熱應力的增大，這一薄層還要發生塑性變形，殘余應力還要變化，來維持身管應力的穩定。可以說，熱應力是殘余應力變化的主要原因，只要熱應力趨于穩定，殘余應力也會趨于穩定，塑性趨于也趨于穩定。

（2）殘余應力的變化規律：一定連發數后，壓縮徑向殘余應力減小，并且內壁局部區域轉變為拉伸徑向殘余應力，在距內壁約2mm身管壓縮切向殘余應力減小，局部區域轉變為拉伸殘余應力，在2mm以外壓縮切向殘余應力增大；冷卻后再連發一定發數后，殘余應力變化不大，只是內壁約0.5mm身管內拉伸切向殘余應力大幅減小。塑性應變的反復變化加劇材料的疲勞，產生損傷以及宏觀裂紋。合理利用塑性變形，既可調整身管的應力分布，又能使身管材料穩定。

（3）減小殘余應力變化程度的策略：控制一次連發數，減小內壁的塑性變形；采用較小的自緊度，減小內壁薄層的應力；采用一定的冷卻方式，減小熱應力的大小；采用高強度炮鋼，減少塑性變形。

［1］姚建軍，徐誠，郭凱.速射武器身管的熱－應力耦合場分析［J］.火炮發射與控制學報，2001（2）：36－39.

YAO Jian－jun，XU Cheng，GUO Kai.The analysis to thermal－stress coupled field in the barrel of rapid fire weapon［J］.Journal of Gun Launch ＆ Control，2001（2）：36－39.

［2］佘建生.槍管輕量化技術研究［D］.太原：中北大學，2002：11－18.

［3］胡振杰.火炮發射過程中的身管熱彈耦合分析［D］.南京：南京理工大學，2007：43－45.

［4］徐亞棟，錢林方，石秀東.復合材料身管三維瞬態熱結構耦合分析［J］.南京理工大學學報，2007，31（2）：350－353.

XU Ya－dong，QIAN Lin－fang，SHI Xiu－dong.Three－dimensional finite element analysis and optimization of composite material barrel［J］.Journal of Nanjing University of Science and Technology，2007，31（2）：350－353.

［5］游仁華.艦炮射擊過程中的瞬態熱響應數值模擬［J］.艦船科學技術，2006，28（6）：53－56.

YOU Ren－hua.Numerical simulation of transient thermal response of barrel when naval gun firing［J］.Ship Science and Technology，2006，28（6）：53－56.

［6］博弈創作室.APDL參數化有限元分析技術及其應用實例［M］.北京：中國水利水電出版社，2004.

［7］奧爾洛夫БВ，拉爾曼ЭК.炮身構造與設計［M］.王天槐，劉淑華，譯.北京：國防工業出版社，1982.

［8］王澤山，何衛東，徐復銘.火藥裝藥設計原理與技術［M］.北京：北京理工大學出版社，2006.

［9］郁圣杰.火炮發射過程中的身管熱分析及其應用［D］.南京：南京理工大學，2004：23－26.