基于修正LuGre模型的反步自適應摩擦補償控制

梁 青，張 劍，王 永

(中國科學技術大學，安徽合肥230027)

0引 言

摩擦是影響機電伺服系統性能的主要因素之一，會導致系統出現穩態誤差、粘滑運動和極限環，因此在高精度伺服系統中必須對摩擦進行補償。

由于靜態摩擦模型只能描述系統處于高速運行時所受的摩擦影響，在系統低速運行時采用靜態摩擦模型會有很大的誤差，因此基于動態摩擦模型的補償方法是實際中較為可行的方法。而如何準確地建立動態摩擦模型是實現動態摩擦補償的關鍵。近年來，國內外學者在摩擦建模方面進行了大量研究，其中比較著名的有 Dahl模型［4］、LuGre 模型［3］、Elasto-plastic 模型［5］、Leuven 模型［6］和 Generalized Maxwell Slip(GMS)模型［7］，其中 LuGre模型由于其模型簡單且在描述低速運行時的摩擦特性較為準確，因此得到了廣泛的應用。然而當系統處于高速運行時系統所受到的摩擦力主要為庫倫摩擦和粘滯摩擦，若仍然采用LuGre模型，必然會使系統的復雜性增加，另外由于溫度、潤滑程度和接觸力等外界條件的變化使得摩擦力矩的參數也會發生變化。目前能同時描述低速和高速狀態時系統所受摩擦影響的摩擦模型并且設計相應的自適應摩擦補償控制器方面的相關文獻較少。

本文采用一種改進的LuGre模型［1］來同時描述系統在低速和高速運行時所受到的摩擦力矩，采用反步自適應算法實現了對摩擦的補償控制，通過仿真并與其他算法比較，驗證了本方法的有效性。

1系統建模

1．1伺服系統模型

若伺服系統除摩擦非線性因素之外不考慮其他非線性因素影響，則伺服系統的動力學方程如下［8］:

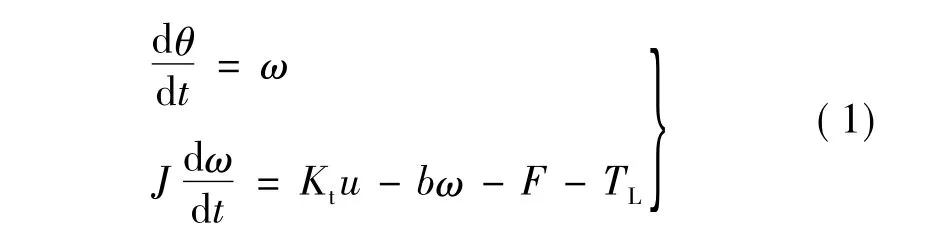
式中:J為等效轉動慣量;b為等效阻尼系數;θ為電機角位置;ω為電機角速度;Kt為電機力矩常數;u系統控制量;F為等效摩擦力矩;TL為等效負載力矩(包括外界擾動作用)。

1．2 系統摩擦力矩模型［1］

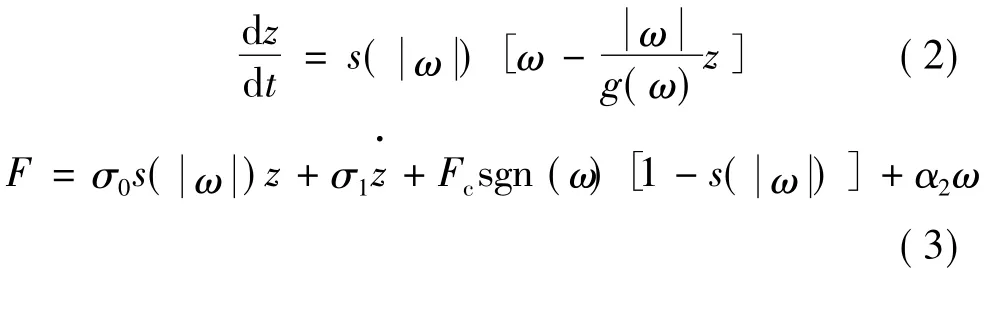
其中:

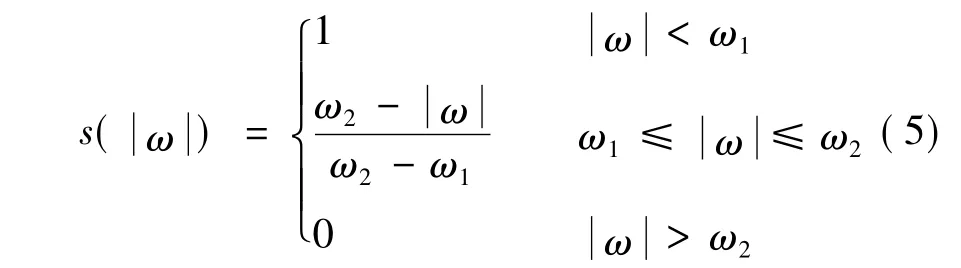
其中:ω2＞ω1＞0。

式(2)～式(4)中，z為接觸表面鬃毛形變量;σ0為鬃毛剛度系數，σ1為鬃毛阻尼系數;Fc為庫倫摩擦系數;Fs為靜摩擦系數;α2為粘性阻尼系數;ωs為Stribeck速度。

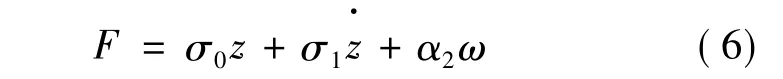
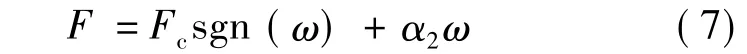
此時系摩擦模型等效于靜態摩擦模型，并且靜態摩擦模型的參數可以不等于LuGre模型中的靜態摩擦模型參數，從而使得該模型具有一定的靈活性。

摩擦受到溫度變化影響會導致參數發生變化［9］，引入ζ來反映參數受到溫度變化的影響。此時摩擦力矩:

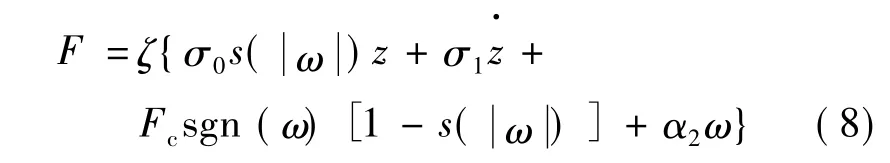
從而伺服系統的模型可表示:

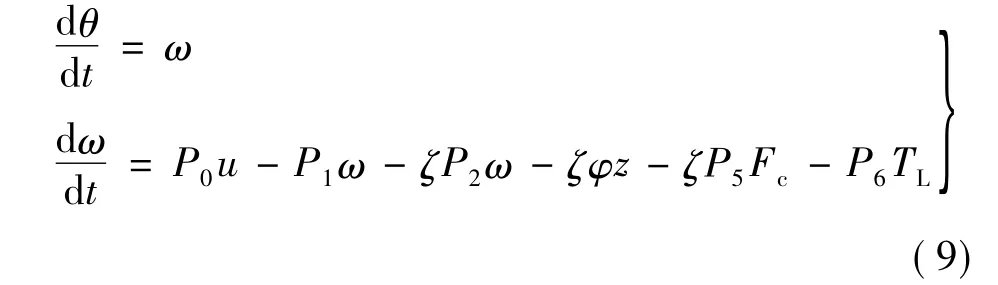
2反步自適應控制器設計

由于LuGre模型的中間變量鬃毛形變量不可直接測量，本文設計一非線性觀測器來估計鬃毛形變量 z，觀測器方程［2，8］:

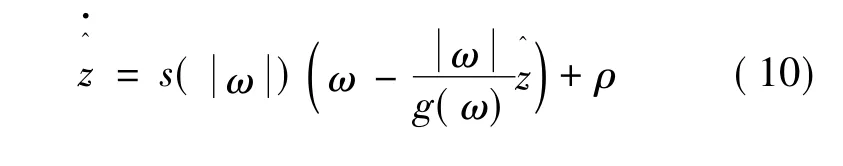
式中:ρ為觀測器的誤差補償項。

定義角位置輸出誤差和角速度誤差:

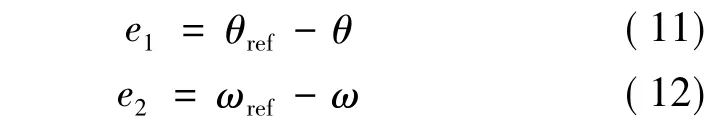
θref為參考位置信號，參考速度信號如下:

為有效地減小摩擦對系統的影響，我們設計如下的控制律和參數自適應律［2，8］:

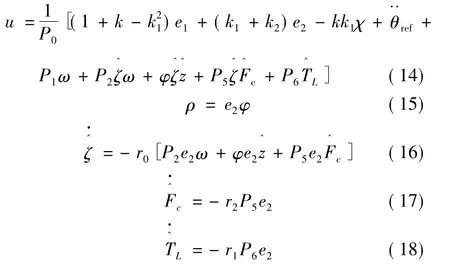
其中:k、k1、k2均大于零。

定理:對于式(9)若采用如式(15)～式(19)的控制律和參數自適應律，則閉環系統是漸近穩定的。

證明:定義如下的Lyapunov函數:

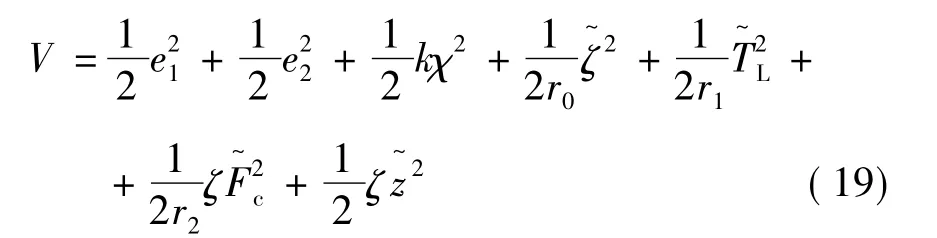
式中:r0＞0，r1＞0，r2＞0，式(19)對時間的微分有:

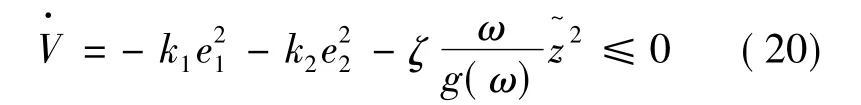
從而系統的閉環穩定性得證。

3仿真分析

仿真主要用來驗證本文所提的基于改進LuGre模型的反步自適應摩擦補償算法的有效性，并與傳統的PID固定摩擦補償方法進行比較。仿真參數設計如下。

伺服系統參數:J=0．9 kg·m2，b=0．3 N·ms/rad，Kt=1，TL=0．5 N·m;摩擦模型參數［2］:σ0=100 N·m，σ1=2．5 N·m，α0=0．28 N·m，α1=0．06 N·m，α2=0．2N·ms/rad，ωs=0．01 rad/s;控制器參數:k1=90，k2=80，k=5，r0=1．2，r1=7．5，r2=10。

為比較控制器補償性能，將本文方法與文獻［9］提到的PID固定摩擦補償方法進行比較。首先設計位置參考信號:θref=sin(πt)，分別使用上述兩種方法進行仿真，仿真結果如圖1和圖2所示。

由圖1、圖2可知，本文所提方法的使得系統跟蹤精度更高、響應更快。為進一步驗證本文算法的有效性，設系統在3～5 s內受到階躍的外界擾動的作用，再次使用上述兩種方法跟蹤正弦信號進行仿真，仿真結果如圖3和圖4所示。

由圖3、圖4可知，當系統受到外界擾動時若采用PID固定摩擦補償控制會使系統出現較大的跟蹤誤差，而本文的方法仍能使系統具有優良的跟蹤性能，因此本文所提方法魯棒性更強。

4結 語

本文采用一種改進的LuGre摩擦模型來描述系統所受摩擦因素的影響，該模型在低速時等效于LuGre模型，在高速時等效于庫倫摩擦+粘滯摩擦，使得模型更符合系統實際所受到的摩擦影響，并降低了摩擦模型的復雜度。本文設計的基于修正LuGre模型的反步自適應摩擦補償控制算法保證了系統在受到摩擦影響時仍具有較高的跟蹤性能，且魯棒性比PID固定摩擦補償方法更強。

［1］ Lu L，Yao B，Wang Q F，et al．Adaptive robust control of linear motors with dynamic friction compensation using modified LuGre model［J］．Automatica，2009(45):2890-2896．

［2］ Tan Y L，Chang J C，Tan H L，Adaptive Backstepping Control and Friction Compensation for AC Servo With Inertia and Load Uncertainties［J］．IEEE Transaction on Industrial Electronics，2003，50(5):944-952．

［3］ de Wit C C，Olsson H，htrom K J．A New Model for Control of Systems with Friction［J］．IEEE Transactions on Automatic Control，1995，40(3):419-425．

［4］ Dahl O．A solid friction model［M］．The Aerospace Corporation，El-Segundo，California，USA，1968．

［5］ Dupont P，Hayward V，Armstrong B，et al．Single state elastoplastic friction models for friction compensation［J］．IEEE Transactions on Automatic Control，2002，47(5):787-792．

［6］ Lampaert V，Swevers J，Al-Bender F．Modification of the Leuven integrated friction model structure［J］．IEEE Transactions on Automatic Control，2002，47(4):683-687．

［7］ Al-Bender F，Lampaert V，Swevers J．The generalized Maxwell slip model:A novel model for friction simulation and compensation［J］．IEEE Transactions on Automatic Control，2005，50(11):1883-1887．

［8］ 周金柱，段寶巖，黃進．LuGre摩擦模型對伺服系統的影響與補償［J］．控制理論與應用，2008，25(6):990-994．

［9］ de Wit C C，Lischinsky P．Adaptive friction compensationwith partially known dynamic friction model［J］．International Journal of A-daptive Control and Signal Process，1997，11(1):65-80．