鋼筋混凝土簡支梁固有頻率的數值計算

楊 斌 谷淡平

0 引言

鋼筋混凝土承彎梁是實際工程中常見的重要構件，其損傷的識別、監測對于確保整個構筑物的安全，評估其服役狀態，都具有重要的意義。深入了解鋼筋混凝土梁的振動特性，是采用動力破損評估法對其損傷進行辨識、監測的前提和基礎[1］。

本文通過振型函數導出了求解梁橫向振動固有頻率的微分方程，在基于組合梁理論的基礎上推導了完整鋼筋混凝土梁固有頻率的計算公式，通過對實際簡支梁進行動力試驗，證實了相關理論和計算公式的正確性，能較好的滿足工程需要。

1 簡支梁固有頻率的計算

梁在橫向荷載作用下，在長為l的梁的軸向(x方向)處用相距無限小的dx兩橫向截面截取一微段，設 y(x，t)，θ(x，t)，M(x，t)和Q(x，t)分別表示梁的x截面處在t時刻的撓度、轉角、彎矩和剪力。它們必須滿足以下微分關系[2］:

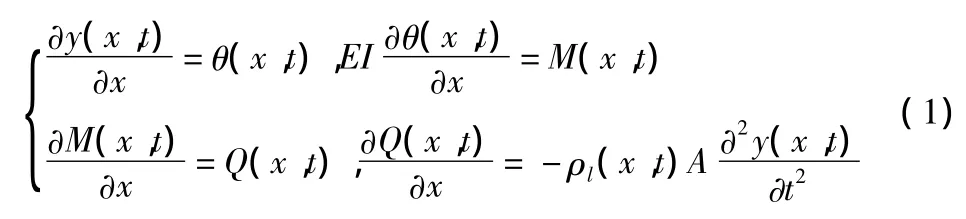
其中，EI(x)，ρl(x)分別為所取微段處的截面抗彎剛度和單位長度的質量。

從式(1)可以得出:

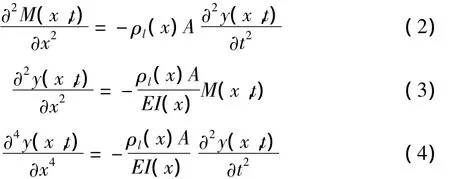
由于梁在任一點、任一時刻的撓度可表示為無數簡諧振動下撓度的疊加，利用分離變量法[3］，設第m階簡諧振動的頻率是ωm，再設Tm(t)，Ym(x)分別為振幅函數和振型函數，則在一定邊界條件下式(4)的解可表示為[4］:

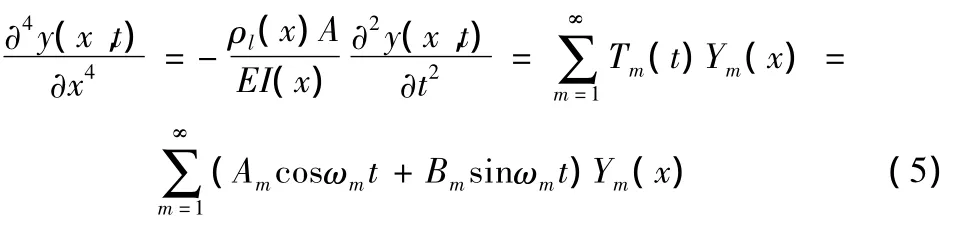
由于撓度函數y(x，t)具有與時間無關而確定的振型特性[5］，為求出各種振型函數對應的頻率，取y(x，t)=(Acosωt+Bsinωt)Y(x)，代入式(4)可得:

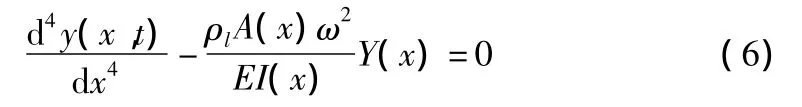
式(6)即為求解梁橫向振動固有頻率的微分方程。

由于EI(x)和ρl(x)在任何截面都相等，則式(6)為四階常系數齊次線性微分方程，求出其通解后根據邊界條件得出積分常數的關系，從而可求出固有頻率ω。……