基于k-最鄰近分類法的灰色評估方法的改進

朱美玲，陳勇明，羅廷友

(成都信息工程學院 數學學院,成都 610225）

0 引言

在預測與決策理論中,評估是極其重要的一個環節。評估方法的種類很多,例如層次分析法、Bayes概率法、模糊評價法、聚類評估等[1],而灰色評估是評估中較為重要的一種。

在評估的研究過程中可以發現,觀測矩陣是評估的主要依據,是評估的出發點。觀測矩陣主要有兩種形式:一是客觀數據,二是專家評分。本文中我們將第二種觀測矩陣稱為專家評分矩陣。現實生活中有很多這樣的例子,如企事業單位的人才招聘,在面試環節往往由有經驗的員工出任考官考察應聘者的專業知識技能、人際關系處理能力、創新能力以及工作態度等各方面的指標,然后利用考官們對各指標的評分進行評估以確定是否錄取應聘對象。對于這類專家評分問題,評價主體——專家在評分過程中往往帶有自身的主觀傾向,如某些專家打分較為保守,對所有對象評分值普遍偏低;同時另一些專家打分又習慣性偏高。而以往的灰色評估方法,無論是經典的灰色聚類評估的主要方法白化權函數和關聯度,還是近年來的一些新的灰色評估方法或者灰色評估方法的改進[2～4]，都沒有考慮到這一點,即在評估過程中沒有考慮如何消除專家主觀因素對結果的影響。針對這一問題,本文擬借鑒k-NN方法,利用每位專家以往的評分記錄修正其當前評分矩陣,消除評分時存在的主觀傾向,使評估更趨于客觀與合理。

1 預備知識

1.1 k-NN的基本原理

定義[5]k-NN(k-Nearest-Neighbor)即k-最鄰近分類法,是數據挖掘中常用的一種算法:在觀測數據集中動態的確定k個與我們希望分類的新觀測相類似的觀測,并使用這些觀測把新觀測分到某一類中。

在使用k-NN方法時,需要先確定一個適當大小的k值。如果k值選取過小,如k=1,則分類方式將對數據的局部特征非常敏感;如果k值選取過大,如k=n(其中n是觀測數據集中觀測的總數),則相當于對大量數據取平均值,同時平滑掉了因單個數據點的噪聲而導致的波動性[5]。因此選擇適當的k值是非常重要的。

1.2 灰色關聯度

定義[6]設系統行為序列S=(s1,s2,…sm),以及

其中，ξ∈(0,1),稱為分辨系數。γh(k)=γ(sh,rhk)表示向量S的第k個分量與Rh第k個分量的關聯度,令

對所有的h=1,2,…,ti計算出γh,得向量：

這里,γh稱為Rh與S的灰色關聯度。

1.3 問題的一般描述

需要考慮的問題的一般描述如下：

設評分主體為某專家組,用集合E={E1,E2,…,Ek}表示;考核指標用集合I={I1,I2,…,Im}表示;當前被考核對象用集合A={A1,A2,…,An}表示。另設專家Ei有ti次歷史評分記錄,將評分值以及相應的最后聚類結果制成表格。不失一般性,為了便于書寫我們此處將評分值的取值范圍定義為區間[1,10]上的整數,基于評分值的聚類標準為:當8≤rhj≤10時,指標Ij歸屬于①類等級;當5≤rhj≤7,指標Ij歸屬于②類等級;1≤rhj≤4,指標Ij歸屬于③類等級,評分值越高對應的類越令人滿意,即①類優于②類,②類優于③類。根據上述規定,制作表1。將第u(u=1,2,…,n)個當前考核對象的評分數據制成表2。

表1 專家Ei歷史評分數據

表2 第u個當前考核對象評分數據

則相應的當前評分矩陣為：

2 基于k-NN方法對當前專家評分矩陣修正的算法和基本原理

2.1 算法的基本原理

為了修正當前被考核對象的專家評分矩陣,首先我們利用關聯度來度量在每位專家的歷史評分數據與其對當前被考核對象Au評分數據的相似度,并選出個數適當的最相似歷史數據,這樣做是因為利用最相似歷史數據而不是全部歷史數據來修正當前專家評分向量,所得的結果將更趨于客觀、合理;其次我們構造修正函數,根據篩選出的每位專家的最相似歷史數據修正其當前評分向量,從而得到修正的專家評分矩陣,繼而進行評估。

2.2 算法

首先,根據關聯度來度量在每位專家以往的評分數據與其對當前被考核對象Au評分數據的相似度。

由表1專家Ei的ti次歷史評分數據,我們得到ti個序列(即專家Ei的ti次歷史評分向量):

另外有專家Ei對被考核對象Au當前評分向量:

根據要求取臨界值γ0,篩選出專家Ei的歷史評分數據中與其對當前考核對象Au評分向量最接近的數據。

經過上述計算后對專家Ei可以得到ki個與當前評分向量相近的歷史評分向量。這里我們借鑒k-NN方法對每個專家Ei利用關聯度從其過去的ti次評分記錄中找到與當前評分最為接近的ki個評分;與其不同的是我們并不事先確定ki值,而是利用關聯度選擇適當的數據后,得到ki的取值。根據k-NN方法對k值的考慮,我們得到ki值以后,根據其大小適當的修正關聯度的臨界值，以保證ki值不是過大或者過小。設修正后ki調整為。將個數據按照取出的順序排列,仍記為仿照表1的做法,我們制作表3

由前文所述知,表3中元素(即評分值)的取值范圍是1到10的整數,表中?是某次考核對某指標經專家組聚類評價后最后劃分所至的類,?的取值是①類、②類或者③類。

將規定的評分值(這里是1到10的正整數)作為列,將規定的類作為行,以評分值在各類出現的次數作為元素,繪制成表4。例如表4中第一行第一列元素n1,1表示表3中評分值為1最后被分至①類的次數,其他以此類推。

下面構造修正函數。構造函數時我們只考慮評分值規定的所屬類別與最終被劃分到的類別是相鄰的。因為實際情況下參加考核的專家具有較為豐富的經驗,對評分的劃分標準有較好的把握,因此不同專家評分時一般不會出現對同一被考核對象給出差異懸殊的評分。構造修正函數如下：

表3 篩選后專家Ei的個相似評分數據

表3 篩選后專家Ei的個相似評分數據

Ei I1 I2 Im REi 1 REi 2?r(i)11?r(i)21?r(i)12?r(i)22?r(i)1m?r(i)2m????REi-ki r(i)-ki1?r(i)-ki2?………?…r(i)-kim ?

表4 專家Ei相似評分數據按類的次數分布

其中,對評分值s修正時s已經確定,不作為變量存在于函數中,fs是對s修正后的評分值,Ns即表4最末一列的元素,即行元素之和,ns1、ns2和ns3為表4中的元素。

3 算法的一般步驟

4 算法實例

設有三個專家對被考核對象的四個指標進行評分,評分標準與前文一致:評分值的取值定義為在區間[1,10]上的整數,基于評分值的聚類標準為:當8≤sj≤10時,指標Ij歸屬于①類;當5≤sj≤7,指標Ij歸屬于②類;1≤sj≤4,指標Ij歸屬于③類(通常評分值越高對應的類越令人滿意)。則專家組用集合E={E1,E2,E3}表示,被考核對象用集合A={A1,A2}表示;考核指標用集合I={I1,I2,I3,I4}表示。先計算被考核對象A1修正的專家評分矩陣,依照同樣方法可以得出A2的修正評分矩陣。

專家E1,E2,E3對被考核對象A1關于指標I1,I2,I3,I4的評分矩陣為：

表5、6、7中的第一行表示指標;第一列表示歷史數據的次數標識;表中元素分為上下兩部分,上面部分是專家評分值,下面部分是最終該指標被劃分的類。

表5 專家E1歷史數據

表6 專家E2歷史數據

表7 專家E3歷史數據

進行計算（k=1,2,3,4;h=1,2,…,11）。取ξ=0.5,計算得

第三步,計算修正的專家評分矩陣。得到的向量個數為k1=5,歷史數據總數n1=11,則不需對k1進行必要的修改。故根據篩選出來的歷史評分向量將表5縮減成表8。

將表8中出現的評分值作為列,將表8中出現的類作為行,以評分值在各類出現的次數作為元素,繪制成表9

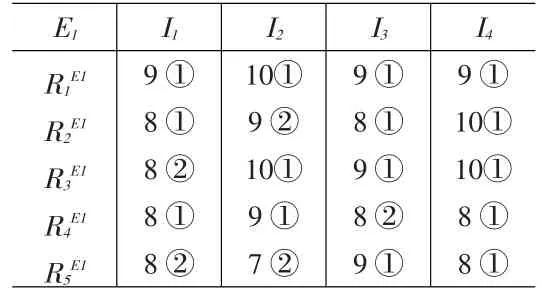
表8 專家E1歷史評分與S1的最相似數據

表9 專家E1相似評分數據按類的次數分布

依據同樣方法，計算E2對A1的當前評分向量S2=(7,9,8,9)的修正評分向量,關聯向量臨界值取γ0=0.8時k2=1,由于k2取值過小,調整關聯向量臨界值γ0=0.7,則k2相應的調整為=4,修正評分向量為E3評分向量S3=(8,9,8,7)的修正評分向量,關聯向量臨界值取γ0=0.8時k3=1,由于k3取值過小,調整關聯向量臨界值γ0=0.5,則k2相應的調整為=4,修正評分向量為

第四步,得到專家E1,E2,E3對被考核對象A1關于指標I1,I2,I3,I4的修正的專家評分矩陣為：

專家E1,E2,E3對被考核對象A2關于指標I1,I2,I3,I4的評分矩陣為：

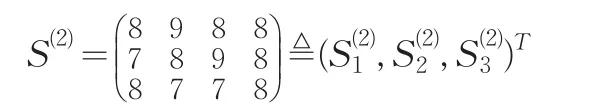
完全依照上面的處理方法,我們得到S(2)修正的專家評分矩陣：

顯然γ1＞γ2,故被考核對象A1優于被考核對象A2。

5 結語

基于k-NN對專家評分矩陣進行修正,以消除專家評分時的主觀傾向（即習慣性偏高或者偏低）可以使得評估的結果更趨于客觀化、合理化。另外值得一提的是,利用本方法得出被考核對象之間的聚類系數更具有可比性。

[1]徐玖平,陳建中.群決策理論與方法實現[M].北京：清華大學出版社,2009.

[2]黨耀國,劉思峰.灰色綜合聚類[J].統計與決策,2004，(10).

[3]李宜敏,羅愛民,呂鳳虎.灰色聚類評估的一種改進方法[J].統計與決策,2007，(1).

[4]王育紅,黨耀國.基于D-S證據理論的灰色定權聚類綜合后評價方法[J].系統工程理論與實踐,2009,29(2).

[5]K.P.Soman,Shyam Diwakar,V.Ajay.數據挖掘基礎教程[M].北京:機械工業出版社,2009.

[6]劉思峰,黨耀國,方志耕,謝乃明.灰色系統理論及應用（第五版）[M].北京：科學出版社,2010.