簡(jiǎn)談二次函數(shù)的綜合應(yīng)用

●

(蘇步青學(xué)校 浙江平陽(yáng) 325404)

簡(jiǎn)談二次函數(shù)的綜合應(yīng)用

●周增強(qiáng)

(蘇步青學(xué)校 浙江平陽(yáng) 325404)

二次函數(shù)是初中數(shù)學(xué)教學(xué)的重要內(nèi)容之一．作為最基本的初等函數(shù)，二次函數(shù)內(nèi)容廣泛，頗受命題者青睞．各地中考試題中二次函數(shù)的考題，既有解析式、值域與最值等基本內(nèi)容，也有通過(guò)與二次方程、二次不等式的聯(lián)系而變化出各種各樣的代數(shù)問(wèn)題；還有大量的從圖像角度、結(jié)合坐標(biāo)系衍生而成的數(shù)形結(jié)合問(wèn)題.這類問(wèn)題綜合性強(qiáng)、難度大，往往以壓軸題的形式出現(xiàn).本文將通過(guò)一些中考試題和模擬題對(duì)二次函數(shù)綜合應(yīng)用進(jìn)行分類說(shuō)明.

1 實(shí)際應(yīng)用題

例1利達(dá)經(jīng)銷店為某工廠代銷一種建筑材料(這里的代銷是指廠家先免費(fèi)提供貨源，待貨物售出后再進(jìn)行結(jié)算，未售出的由廠家負(fù)責(zé)處理)．當(dāng)每噸售價(jià)為260元時(shí)，月銷售量為45噸.該經(jīng)銷店為提高經(jīng)營(yíng)利潤(rùn)，準(zhǔn)備采取降價(jià)的方式進(jìn)行促銷.經(jīng)市場(chǎng)調(diào)查發(fā)現(xiàn)：當(dāng)每噸售價(jià)下降10元時(shí)，月銷售量就會(huì)增加7.5噸．綜合考慮各種因素，每售出1噸建筑材料共需支付廠家及其他費(fèi)用100元.設(shè)每噸材料售價(jià)為x(元)，該經(jīng)銷店的月利潤(rùn)為y(元).

(1)當(dāng)每噸售價(jià)為240元時(shí)，計(jì)算此時(shí)的月銷售量；

(2)求出y與x的函數(shù)關(guān)系式(不要求寫出x的取值范圍)；

(3)該經(jīng)銷店要獲得最大月利潤(rùn)，售價(jià)應(yīng)定為每噸多少元？

(4)小靜說(shuō)：“當(dāng)月利潤(rùn)最大時(shí)，月銷售額也最大”,你認(rèn)為對(duì)嗎？請(qǐng)說(shuō)明理由.

解(1)由題意得，月銷售量為

45+(260-240)×7.5÷10=60(噸).

(2)根據(jù)題意得

即

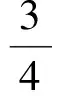
(3)對(duì)第(2)小題的結(jié)論配方得

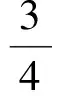
因此利達(dá)經(jīng)銷店要獲得最大月利潤(rùn)，材料的售價(jià)應(yīng)定價(jià)為每噸210元.

(4)小靜說(shuō)的不對(duì).當(dāng)月利潤(rùn)最大時(shí)，x為210元，此時(shí)月銷售額為17 325元；當(dāng)x為200元時(shí)，月銷售額為18 000元.因?yàn)?/p>

17 325lt;18 000，

所以當(dāng)月利潤(rùn)最大時(shí)，月銷售額不是最大，故小靜說(shuō)的不對(duì).

說(shuō)明這是二次函數(shù)的性質(zhì)在實(shí)際問(wèn)題中的應(yīng)用.解這類題型的重點(diǎn)是列出二次函數(shù)的關(guān)系式，然后運(yùn)用二次函數(shù)的性質(zhì)解題.

2 動(dòng)點(diǎn)運(yùn)動(dòng)問(wèn)題

圖1

(1)求這條拋物線的函數(shù)關(guān)系式.

(2)2個(gè)動(dòng)點(diǎn)P，Q分別從點(diǎn)O，A同時(shí)出發(fā),以每秒1個(gè)單位長(zhǎng)度的速度運(yùn)動(dòng).其中點(diǎn)P沿著線段OA向點(diǎn)A運(yùn)動(dòng)，點(diǎn)Q沿著折線A→B→C的路線向點(diǎn)C運(yùn)動(dòng).設(shè)這2個(gè)動(dòng)點(diǎn)運(yùn)動(dòng)的時(shí)間為t(秒)(0lt;tlt;4)，△PQA的面積記為S.

①求S與t的函數(shù)關(guān)系式.

②當(dāng)t為何值時(shí)，S有最大值，最大值是多少？并指出此時(shí)△PQA的形狀.

③是否存在這樣的t值，使得△PQA是直角三角形?若存在，請(qǐng)直接寫出此時(shí)點(diǎn)P,Q的坐標(biāo)；若不存在，請(qǐng)說(shuō)明理由.

解得

故所求拋物線的函數(shù)關(guān)系式為

(2)①過(guò)點(diǎn)B作BE⊥x軸于點(diǎn)E，則

∠BAE=60°.

1°當(dāng)點(diǎn)Q在線段AB上運(yùn)動(dòng)，即0lt;t≤2時(shí)，

QA=t，PA=4-t.

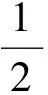
綜合1°，2°可得

②1°當(dāng)0lt;t≤2時(shí)，

2°當(dāng)2≤tlt;4時(shí)，

③存在.當(dāng)點(diǎn)Q在線段AB上運(yùn)動(dòng)時(shí)，要使得△PQA是直角三角形，必須使得∠PQA=90°，這時(shí)PA=2QA，即

4-t=2t，

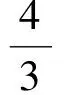
說(shuō)明該動(dòng)點(diǎn)問(wèn)題的解題思路是先利用二次函數(shù)描述動(dòng)點(diǎn)的運(yùn)動(dòng)規(guī)律，然后再具體運(yùn)算求解.

3 含參數(shù)問(wèn)題

例3已知y2=4a(x-a)(agt;0)，且當(dāng)x≥a時(shí)，S=(x-3)2+y2的最小值為4，求參數(shù)a的值．

解將y2=4a(x-a)代入S的表達(dá)式中，得

S=(x-3)2+4a(x-a)=

x2-2(3-2a)x+9-4a2=

[x-(3-2a)]2+12a-8a2,

則S是關(guān)于x的二次函數(shù)，其定義域?yàn)閤gt;a，對(duì)稱軸方程為x=3-2a，頂點(diǎn)坐標(biāo)為(3-2a,12a-8a2)，圖像開(kāi)口向上．

若3-2a≥a，即0lt;a≤1,則當(dāng)x=3-2a時(shí)，

S最小=12a-8a2=4,

此時(shí)

若3-2alt;a，即agt;1,則當(dāng)x=a時(shí)，

S最小=[a-(3-2a)]2+12a-8a2=4,

此時(shí)

a=5或a=1(因agt;1,故a=1舍去).

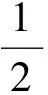
說(shuō)明函數(shù)中的參數(shù)問(wèn)題一般是先對(duì)參數(shù)范圍進(jìn)行分析，再結(jié)合函數(shù)性質(zhì)獲得等量關(guān)系進(jìn)行求解．

4 圖形信息題

例4某公司推出了一種高效環(huán)保型除草劑，年初上市后，公司經(jīng)歷了從虧損到盈利的過(guò)程.圖2的二次函數(shù)圖形(部分)表示了該公司年初以來(lái)累積利潤(rùn)S(萬(wàn)元)與時(shí)間t(月)之間的關(guān)系(即前t個(gè)月的利潤(rùn)總和S與t之間的關(guān)系).

根據(jù)圖形提供信息，解答下列問(wèn)題：

(1)公司從第幾個(gè)月末開(kāi)始扭虧為盈；

(2)累積利潤(rùn)S與時(shí)間t之間的函數(shù)關(guān)系式；

(3)求截止到何月末公司累積利潤(rùn)可達(dá)30萬(wàn)元；

(4)求第8個(gè)月公司所獲利是多少元？

圖2

解(1)由圖2可知公司從第4個(gè)月末以后開(kāi)始扭虧為盈.

(2)由圖2可知頂點(diǎn)坐標(biāo)為(2,-2)，可設(shè)其函數(shù)關(guān)系式為

y=a(t-2)2-2.

因?yàn)樗蠛瘮?shù)關(guān)系式的圖形過(guò)點(diǎn)(0,0)，所以

a(t-2)2-2=0,

解得

從而所求函數(shù)關(guān)系式為

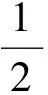
即

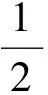
t1=10，t2=-6(舍去),

因此截止到10月末公司累積利潤(rùn)可達(dá)30萬(wàn)元.

(4)把t=7代入關(guān)系式，得

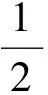
把t=8代入關(guān)系式，得

因?yàn)?/p>

16-10.5=5.5.

所以第8個(gè)月公司所獲利是5.5萬(wàn)元.

說(shuō)明圖形信息題顧名思義是指圖形中蘊(yùn)含著條件信息，一般通過(guò)圖形中已知的點(diǎn)坐標(biāo)，根據(jù)合適的二次函數(shù)表達(dá)式列出二次函數(shù)，從而使問(wèn)題獲解．

5 代數(shù)推理題

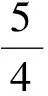
證明因?yàn)閒(-1)=a-b+c,

f(1)=a+b+c,f(0)=c,

所以

當(dāng)-1≤x≤0時(shí)，

-x2-x+1=

當(dāng)0≤x≤-1時(shí)，

-x2+x+1=

綜上所述，問(wèn)題獲證.

6 探索性問(wèn)題

圖3

(1)求點(diǎn)D的坐標(biāo).

(2)求經(jīng)過(guò)點(diǎn)O，B，D的拋物線解析式.

(3)判斷在第(2)小題中所得的拋物線上是否存在一點(diǎn)P，使得ΔDCP∽ΔOCD？若存在，求出點(diǎn)P的坐標(biāo)；若不存在，請(qǐng)說(shuō)明理由．

解(1)連結(jié)AD，則AD⊥CD于點(diǎn)D,作DE⊥OA于點(diǎn)E．由點(diǎn)A的坐標(biāo)為(1，0)，且OC=2OA，可得AC=3，因此

于是

解得

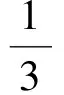
因而

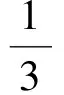
得

解得

故所求拋物線的解析式為

(3)設(shè)⊙A與x軸的另一個(gè)交點(diǎn)為F(2,0)，連結(jié)DF. 由CD切⊙A于點(diǎn)D，得

∠CDO=∠CFD.

又∠DCO=∠FCD，因此

△OCD∽△DCF.

說(shuō)明二次函數(shù)探索性問(wèn)題的解法并不唯一，重點(diǎn)是找到條件間的關(guān)系，對(duì)每一個(gè)已知條件進(jìn)行分析利用．在探索性問(wèn)題中比較常見(jiàn)的是存在性問(wèn)題，這類問(wèn)題的一般解法有2種，一是假設(shè)結(jié)論存在，若求出的結(jié)論符合已知條件，則結(jié)論存在；若求出結(jié)論不符合已知條件或與定理、公理等相矛盾，則結(jié)論不存在．二是像本題這樣，先找到特殊點(diǎn)(或特殊值)等，然后證明這些點(diǎn)或值就是解決問(wèn)題所需要的.

[1] 梁麗平，安振平.二次函數(shù)綜合問(wèn)題例談[J].數(shù)理化學(xué)習(xí)(高中版),2006(1):2-6.

[2] 顧國(guó)璽.二次函數(shù)知識(shí)的綜合應(yīng)用[J].數(shù)理化解題研究(初中版),2011(2):18-20.